§ 33. Конденсаторы. Возьмем две изолированные металлические пластины 1 и 2 (рис. 58), расположенные на некото
ром расстоянии друг от друга, и зарядим их равными разноименными зарядами. Это можно сделать разными способами. Например, можно присоединить пластины к полюсам электрической машины. На одну из пластин при этом перейдет некоторый отрицательный Заряд, т. е. добавится некоторое избыточное число электронов, а на другой появится равный ему по модулю положительный заряд, т. е. соответствующее число электронов будет удалено из пластины.
К
электрической машине
Рис.
58. Опыт по изучению зависимости емкости
конденсатора от расстояния между
его пластинами: а)
при сдвигании пластин емкость конденсатора
увеличивается; листки электрометра
спадают, хотя заряд остается прежним;
б)
схема опыта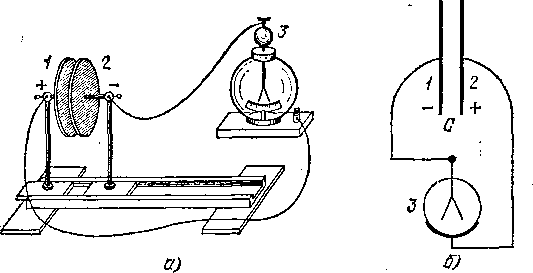
Можно поступить иначе: одну из пластин соединить с Землей (например, соединить ее металлической проволокой с водопроводным краном), а к другой пластине прикоснуться заряженным телом. При этом вследствие индукции (§ 8) на заземленной пластине также появится заряд, равный заряду на другой пластине, но противоположный по знаку.
При любом способе зарядки пластин все происходит так, как если бы некоторый заряд был перенесен с одной пластины на другую. Система двух разноименно заряженных проводников называется конденсатором, а заряд, который надо перенести с одного проводника на другой, чтобы зарядить один из них отрицательно, а другой положительно, называется зарядом конденсатора. В частности, плоским конденсатором называется конденсатор, состоящий из двух параллельных пластин, расстояние между которыми мало по сравнению с размерами пластин.
Разность потенциалов между пластинами конденсатора, конечно, зависит от заряда конденсатора. Присоединив к пластинам 1 и 2 конденсатора электрометр 5 и увеличивая заряд конденсатора повторной зарядкой, мы найдем,' что показания электрометра тем больше, чем больший заряд мы сообщаем конденсатору. Измеряя заряд q (например, по методу, изложенному в § 10) и разность потенциалов U (например, с помощью электрометра), мы убедимся на опыте, что разность потенциалов U между пластинами прямо пропорциональна заряду q, находящемуся на каждой из них, и поэтому зависимость между этими величинами может быть представлена формулой
q = CU. (33.1)
Здесь С — коэффициент, характеризующий конденсатор. Нетрудно видеть, какой физический смысл имеет этот коэффициент. Если мы подберем такой заряд q, чтобы между пластинами конденсатора возникла разность потенциалов, равная единице, то из формулы (33.1) получим C=q. Таким образом, величина С определяет тот заряд, который необходим, чтобы зарядить конденсатор до разности потенциалов, равной единице. Поэтому коэффициент С но-' сит название электрической емкости конденсатора или просто его емкости. Отсюда следует, что емкость конденсатора есть отношение заряда конденсатора к той разности потенциалов, которую этот заряд сообщает конденсаторуг
С = (33.2)
В СИ единица емкости носит в честь Фарадея название фарад (Ф). Емкостью, равной одному фараду, обладает •' такой конденсатор, между пластинами которого возникает разность потенциалов, равная одному вольту, при заряде на каждой из пластин, равном одному кулону:
1 Ф = 1 Кл/1 В. (33.3)
Для практических целей эта единица слишком велика, и на практике обычно применяются более мелкие единицы емкости — микрофарад (мкФ), равный одной миллионной доле фарада, и пикофарад (пФ), равный одной миллионной доле микрофарада. Таким образом,
1 ф = Ю8 мкФ = 1012 пФ, 1 мкФ = 10-в Ф,
пФ — 10-6 мкФ = 10“12 Ф.