§ 31. Распределение зарядов в проводнике. Клетка Фарадея.

Мы видели, что поверхность проводника, как нейтрального, так и заряженного, является эквипотенциальной поверх­ностью (§ 24) и внутри проводника напряженность поля равна нулю (§ 16) *). То же относится и к полому провод­нику: поверхность его есть поверхность эквипотенциаль­ная и поле внутри полости равно нулю, как бы сильно ни был заряжен проводник, если, конечно, внутри полости нет изолированных от проводника заряженных тел.

Этот вывод был наглядно продемонстрирован англий­ским физиком Майклом Фарадеем (1791—1861), обогатив­шим науку рядом крупнейших открытий. Его опыт состоял в следующем. Большая деревянная клетка была оклеена листами станиоля (оловянной бумагой), изолирована, от Земли и сильно заряжена при помощи электрической ма­шины. В клетку помещался сам Фарадей с очень чувстви­тельным электроскопом. Несмотря на то, что с внешней по­верхности клетки при приближении к ней тел, соединенных с Землей, вылетали искры, указывая этим на большую раз­ность потенциалов между клеткой и Землей, электроскоп внутри клетки не показывал никакого отклонения (рис. 53);

*) Это справедливо только в случае равновесия зарядов на про­воднике. (Примеч. ред.)

гг

Видоизменение этого опыта показано на рис. 54. Если сделать из металлической сетки замкнутую полость и при­весить листочки бумаги с внутренней и внешней сторон по­лости, то обнаружим, что отклоняются лишь наружные

Рис. 53. Опыт Фарадея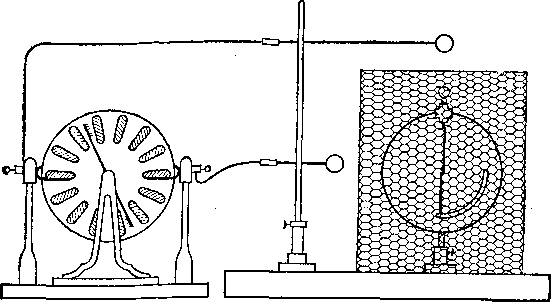

К электрической машине

Рис. 54. Видоизменение опыта Фа­радея. Металлическая клетка заря­жена. Листочки бумаги снаружи отклоняются, указывая на наличие заряда на внешних поверхностях стен клетки. Внутри клетки заряда нет, листочки бумаги не отклоня­ются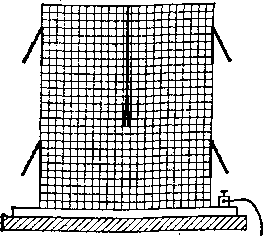

Рис. 55. Исследование распре­деления заряда в проводнике 1 при помощи пробной пластин­ки 2. Внутри полости проводни­ка заряда нет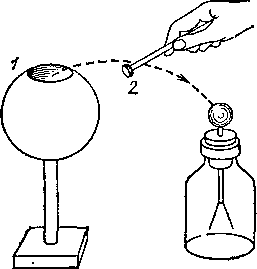

лист очки. Это показывает, что электрическое поле суще­ствует только в пространстве между клеткой и окружающи­ми ее предметами, т. е. снаружи клетки; внутри же клетки поле отсутствует.

При зарядке любого проводника заряды распределяют­ся в нем так, что электрическое поле внутри него исчезает, и разность потенциалов между любыми точками обращает­ся в нуль. Посмотрим, каким образом для этого должны разместиться заряды.

Зарядим полый проводник, например полый изолиро­ванный шар 1 (рис. 55), имеющий небольшое отверстие. Возьмем маленькую металлическую пластинку 2, укреп­ленную на изолирующей ручке («пробную пластинку»), коснемся ею какого-либо места внешней поверхности шара и затем приведем в соприкосновение с электроскопом. Лист­ки электроскопа разойдутся на некоторый угол, указывая этим, что пробная пластинка при соприкосновении с шаром зарядилась. Если мы, однако, коснемся пробной пластинкой внутренней поверхности шара, то пластинка будет оста­ваться незаряженной, как бы сильно ни был заряжен шар. Почерпнуть заряды можно только с внешней поверхности проводника, а с внутренней это оказывается невозмож­ным. Более того, если мы предварительно зарядим проб­ную пластинку и коснемся ею внутренней поверхности про­водника, то весь заряд перейдет на этот проводник. Это про­исходит независимо от того, какой заряд уже имелся на проводнике. В § 19 мы подробно разъяснили это явление. Итак, в состоянии равновесия заряды распределяются толь­ко на внешней поверхности проводника. Конечно, если бы мы повторили с полым проводником 'опыт, изображенный на рис. 45, касаясь проводника концом проволоки, веду­щей к электрометру, то убедились бы, что вся поверхность проводника, как внешняя, так и внутренняя, есть поверх­ность одного потенциала: распределение зарядов по внеш­ней поверхности проводника есть результат действия элек­трического поля. Только тогда, когда весь заряд перейдет на поверхность проводника, установится равновесие, т. е. внутри проводника напряженность поля сделается равной нулю и все точки проводника (внешняя поверхность, внут­ренняя поверхность и точки в толще металла) будут иметь один и тот же потенциал.

Таким образом, проводящая поверхность вполне защи­щает область, которую она окружает, от действия электри­ческого поля, созданного зарядами, расположенными на этой поверхности или вне ее. Линии внешнего поля оканчи­ваются на этой поверхности, в проводящем слое они не мо­гут проходить, и внутренняя полость оказывается сво­бодной от поля. Поэтому такие металлические поверхнос­ти называются электростатическими защитами. Интересно

отметить, что даже поверхность, сделанная из металли­ческой сетки, может служить защитой, если только сетка достаточно густа.

1. В центре полого изолированного металлического шара нахо­дится заряд. Отклоните^ ли заряженный грузик, подвешенный на шелковой нити и помещенный вне шара? Разберите подробно, что при этом происходит. Что будет, если шар заземлен?

2. Почему пороховые склады для защиты от удара молний ок­ружают со всех сторон заземленной металлической сеткой? Поче­му введенные в такое здание водопроводные трубы должны быть также хорошо заземлены?

Рис. 56

ройства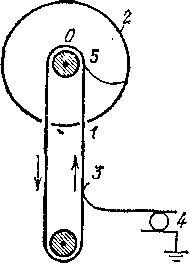

Тем обстоятельством, что заряды распределяются на внешней поверхности проводника, часто пользуются на практике. Когда желают полностью перенести заряд како­го-нибудь проводника*на электроскоп (или электрометр), то к электроскопу присоединяют по возможности замкну­тую металлическую полость и вводят заряженный провод­ник внутрь этой полости. Проводник полностью разряжа­ется, и весь его 'заряд переходит на электроскоп. Это приспособление в честь Фарадея на­зывают «фарадеевым цилиндром», так как на практике эта полость чаще всего выполняется в виде металли­ческого цилиндра. Мы уже пользо­вались этим свойством фарадеева цилиндра (стакана) в опыте, изобра­женном на рис. 9, и подробно разъ­яснили его в § 1£L

Принцип уст- генератора

Ван-де-Граафа

Ван-де-Грааф предложил использовать свойства фарадеева цилиндра для получе­ния очень высоких напряжений. Принцип действия его генератора показан на рис. 56. Бесконечная лента 1 из какого-нибудь изоли­рующего материала, например шелка, движет­ся при помощи мотора на двух роликах и одним своим концом заходит внутрь полого, изолированного от Земли металлического шара 2. Вне шара лента при помошСи кисточки 3 заряжается каким-либо источником, например бата­реей или электрической машиной 4, до напряжения 30—50 кВ относи­тельно Земли, если второй полюс батареи или машины заземлен. Внутри шара 2 заряженные участки ленты касаются кисточки 5 и полностью от­дают шару свой заряд, который сейчас же перераспределяется по внеш­ней поверхности шара. Благодаря этому ничто не препятствует непре* рывному переносу заряда на шар. Напряжение между шаром 2 и Зем­лей непрерывно увеличивается. Таким образом можно получить напря­жение в несколько миллионов вольт. Подобные машины применяли в опытах по расщеплению атомных ядер,

?31.3. Мог бы описанный выше генератор Ван-де-Граафа рабо­тать, если бы шар его был сделан из изолирующего материала или если бы транспортерная лента в нем была проводящей (ме­таллической)?

а

Рис. 57. Распределение поверх­ностной плотности заряда на проводнике сложной формы. Ес­ли для наглядности представить себе, что проводник окружен слоем, толщина которого про­порциональна поверхностной плотности заряда, то получит­ся фигура, изображенная штри­ховой линией

§ 32. Поверхностная плотность заряда. Исследуем те­перь на опыте, каким образом распределяются заряды на внешней поверхности проводника. Для этого мы восполь­зуемся по-прежнему пробной пластинкой. Она должна быть гибкой или настолько малой, чтобы при соприкосно­вении с проводником ее можно было рассматривать как часть поверхности проводника. В этом случае на нее перей­дет заряд, приходящийся на часть поверхности, совпадаю­щей с пластинкой. Отношение этого заряда к площади, ко­торую он занимает, определяет количество электричества, приходящееся на единицу поверхности в исследуемом мес­те. Эту величину называют поверхностной плотностью заряда в данном месте. Перенося пластинку в фарадеев цилиндр электрометра, мы сможем по отклонению лист­ков судить о поверхностной плотности заряда.

Касаясь пробной пластин­кой различных точек заряжен­ного шара, можно убедиться, что поверхностная плотность заряда на шаре одна и та же во всех местах. Заряд рас­пределяется по внешней по­верхности шара равномерно.

Для проводников, более сложной формы распределение плотности заряда более сложно. Заряжая проводник, изоб­раженный на рис. 57, и касаясь пробной пластинкой его боковой поверхности'й, вогнутой части Ь и области, оканчи­вающейся острием с, мы найдем, что поверхностная плот­ность заряда у проводника произвольной формы различна для разных участков поверхности. Наименьшее значение она имеет на вогнутой поверхности, наибольшее — на выступающих остриях. Напоминаем еще раз, что хотя по­верхность такого проводника является эквипотенциальной (§ 24), плотность распределенного заряда на нем может быть весьма неравномерна.