5.3.5 Понятие о системе нескольких случайных величин и их числовых характеристиках

До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Величины, возможные значения которых определяются двумя, тремя, ..., n числами, называются, соответственно, двумерными, трехмерными, ..., n-мерными.

Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично n-мерную величину можно рассматривать как систему n случайных величин. Например, трехмерная величина (X, Y, Z) определяет систему трех случайных величин X, Y и Z.

Целесообразно различать дискретные (составляющие этих величин дискретны) и непрерывные (составляющие этих величин непрерывны) многомерные случайные величины.

Две случайные величины независимы, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, пользуются и другими характеристиками, к числу которых относятся корреляционный момент и коэффициент корреляции.

Корреляционным моментом _xy случайных величин X и Y называют математическое ожидание произведения отклонений этих величин

_xy = M[(X – M(X))(Y – M(Y))]. (5.26)

Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент равен нулю, если X и Y незави­симы. Если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.

Коэффициентом корреляции r_ху случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратичных отклонений этих величин

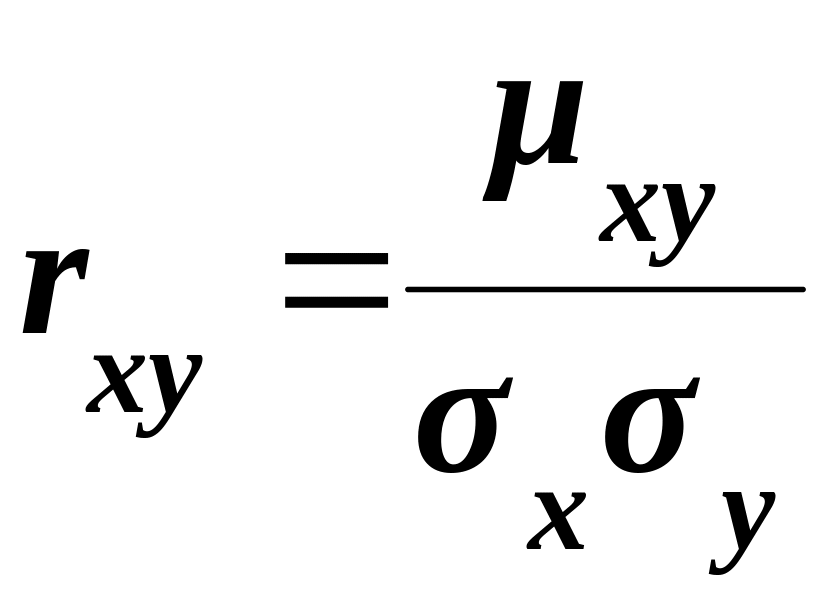. (5.27)

Так как размерность r_ху равна произведению размерностей величин X и Y, _х имеет размерность величины X, _у имеет размерность величины Y, то r_ху – безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом. Коэффициент корреляции независимых слу­чайных величин равен нулю (так как _xy = 0).

Две случайные величины X и Y называют коррелированными, если их корреляционный момент (или – коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Обратное предположение не всегда имеет место, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.

Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Заметим, однако, что из некоррелированности нормально распределенных величин вытекает их независимость.

То есть, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности – равносильны.

Нормальный закон распределения на плоскости определяется пятью параметрами: a₁, а₂, _х, _y и r_xy. Эти параметры имеют следующий вероят­ностный смысл:

a₁, а₂ – математические ожидания;

_х, _y – средние квадратичные отклонения;

r_xy – коэффициент корреляции величин X и Y.