Варианты хi 2 6 10 частоты ni 12 18 30.

Решение. Найдем объем выборки: 12 + 18 + 30 = 60. Наименьшая варианта равна 2, следовательно,

= 0 при х < 2.

Значение Х < 6, а именно: x₁ = 2 наблюдалось 12 раз, следовательно,

при 2 < x  6.

Значения Х < 10, а именно: x₁ = 2 и x₂ = 6 наблюдались 12 + 18 = 30 раз, следовательно,

при 6 < x  10.

Так как х = 10 – наибольшая варианта, то

= 1 при х > 10.

Искомая эмпирическая функция

График этой функции изображен на рис. 5.5.

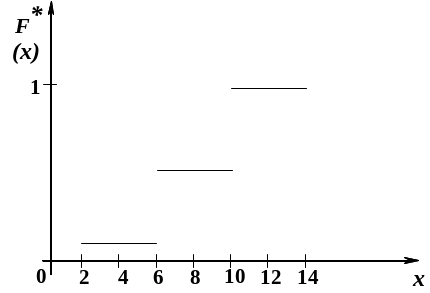
Рис. 5.5.

5.4.4 Полигон и гистограмма

В целях наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), ..., (x_k, n_k). Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат – соответствующие им частоты n_i. Точки (x_i, n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁, W₁), (x₂, W₂),..., (x_k, W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, a на оси ординат соответствующие им относительные частоты W_i.

Точки (x_i, W_i) соединяют отрезками прямых и получают полигон относительных частот (рис. 5.6).

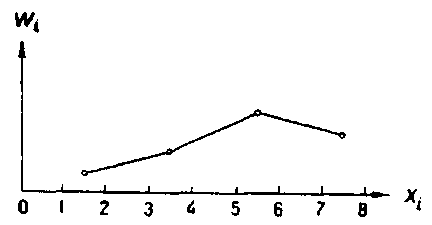
Рис. 5.6.

В ряде случаев, в частности, в случае непрерывного признака, целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиною h и находят для каждого частичного интервала n_i, т.е. сумму частот вариант, попавших в i-й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-гo частичного прямоугольника равна  сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (рис. 5.7). Площадь i-го частичного прямоугольника равна – относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

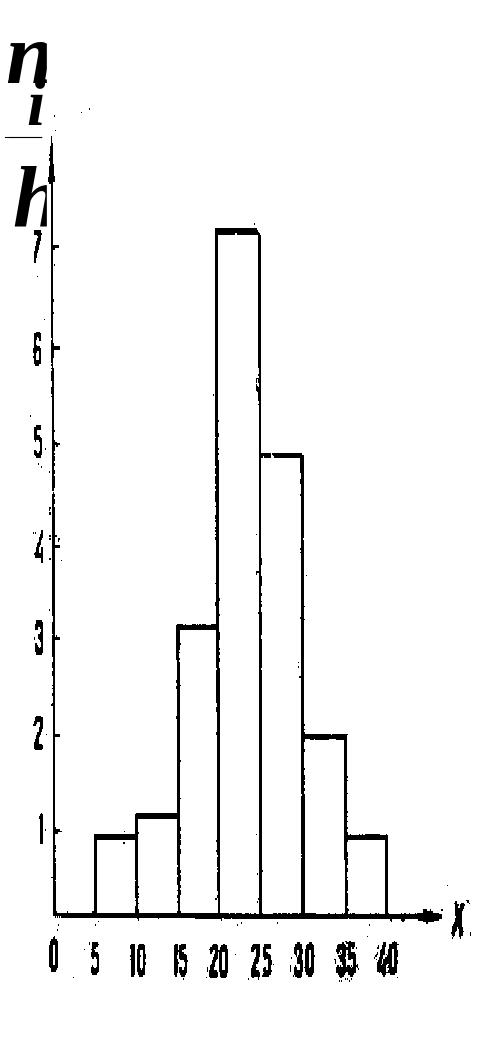
Рис. 5.7.

5.4.5 Статистические оценки параметров распределения

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того, чтобы статистические оценки давали “хорошие” приближения оцениваемых параметров, они должны соответствовать определенным требованиям. Ниже указаны эти требования.

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т. е.

(5.30)

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при n стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n стремится к нулю, то такая оценка оказывается и состоятельной.

Пусть изучается дискретная генеральная совокупность относительно количественного признака X.

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения х₁, х₂, ..., х_k признака выборки объема n различны, то

(5.31)

Если же значения признака х₁, х₂, ..., х_k имеют, соответственно, частоты n₁, n₂, ..., n_k, то

, или , (5.32)

т.е. выборочная средняя является средней взвешенной значений признака с весами, равными соответствующим частотам.

Выборочная средняя – несмещенная оценка генеральной средней.

При увеличении объема выборки n выборочная средняя стремится по вероятности к генеральной средней, а это и означает, что выборочная средняя является состоятельной оценкой генеральной средней. Если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.

Чем объем выборки больше, тем меньше выборочная средняя отличается от генеральной.

Допустим, что все значения количественного признака X совокупности, безразлично генеральной или выборочной, разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.

Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.

Общей средней называют среднее арифметическое значений признака, принадлежащих всей совокупности.

Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения х₁, х₂, ..., х_k признака выборки объема n различны, то

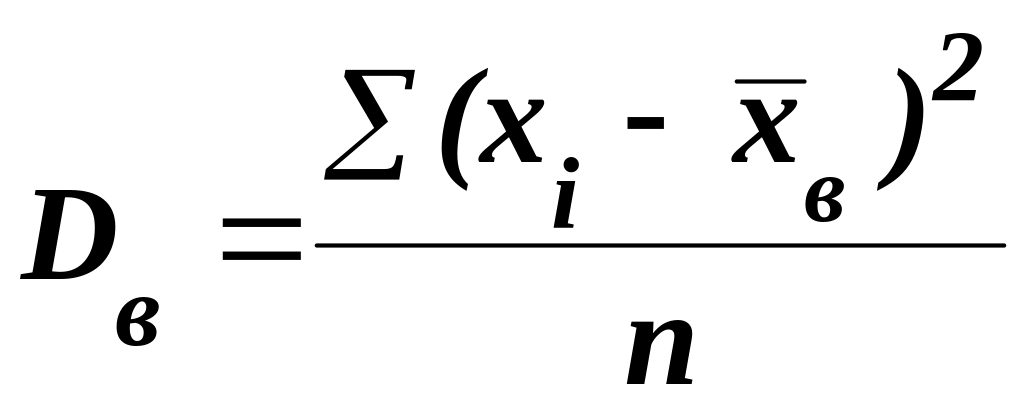. (5.33)

Если же значения признака х₁, х₂, ..., х_k имеют, соответственно, частоты n₁, n₂, ..., n_k, причем, n₁ + n₂ + ... + n_k = n, то

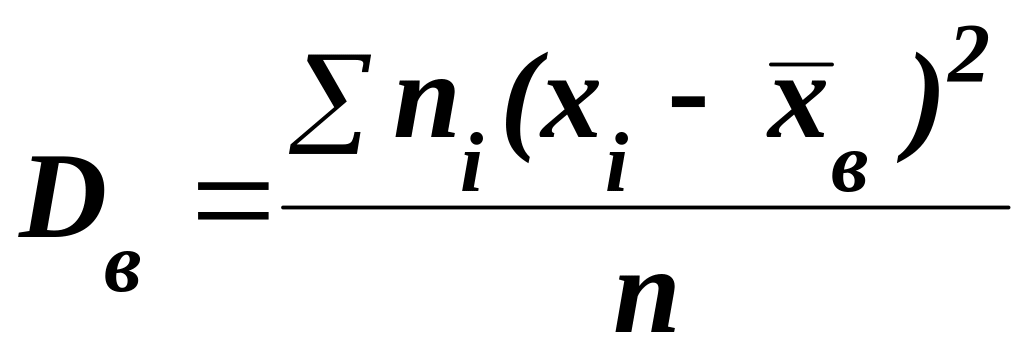, (5.34)

т. е. выборочная дисперсия – средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

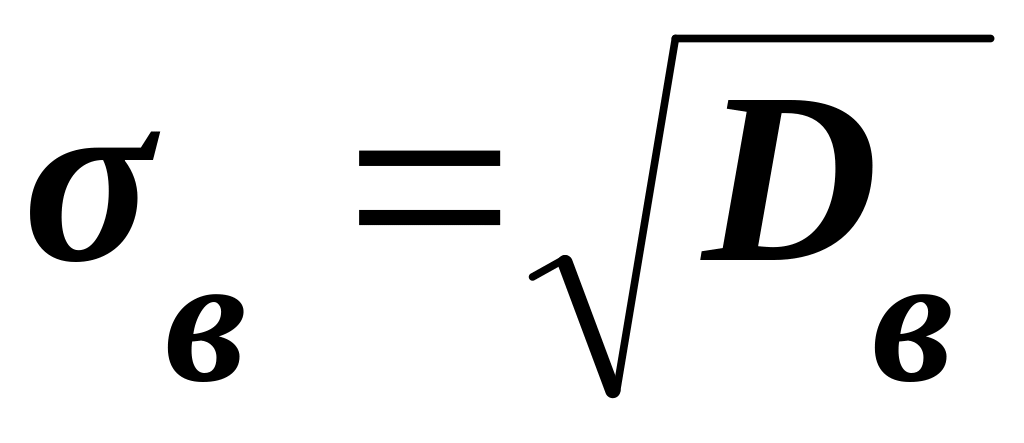. (5.35)

Выборочная дисперсия является смещенной оценкой генеральной дисперсии , другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

(5.36)

Легко “исправить” выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить D_в на дробь .

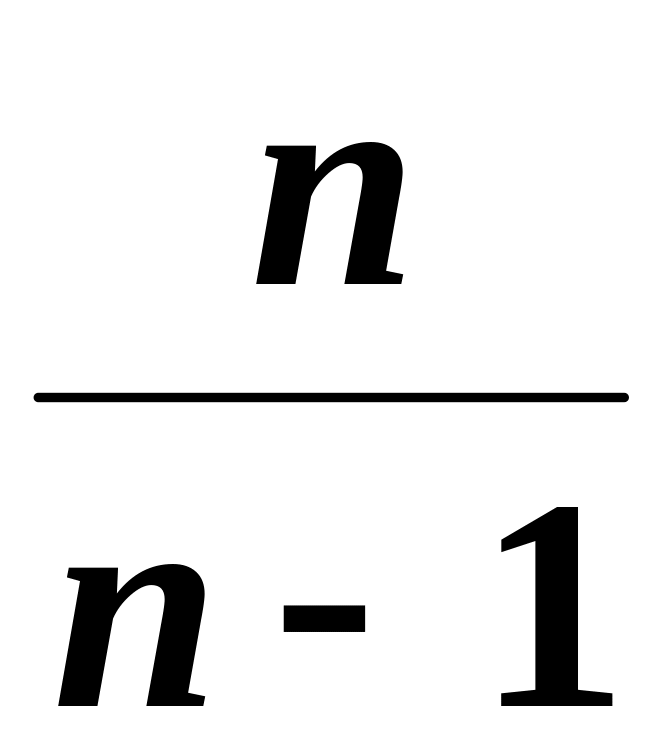Сделав это, получим “исправленную дисперсию”, которую обычно обозначают через

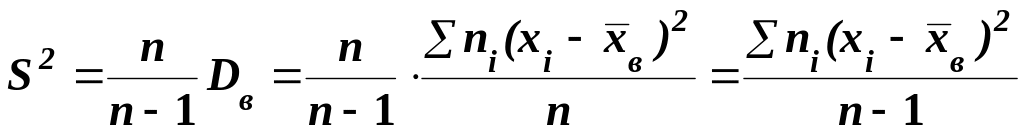(5.37)

Исправленная дисперсия является несмещённой оценкой генеральной дисперсии.

Для оценки среднего квадратичного отклонения генеральной совокупности используют “исправленное” среднее квадратичное отклонение, которое равно квадратному корню из исправленной дисперсии:

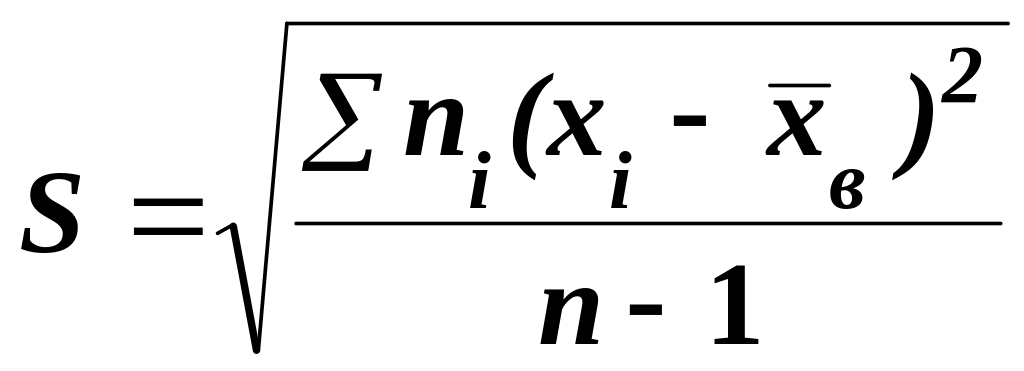. (5.38)

S не является несмещенной оценкой; чтобы отразить этот факт, далее будем писать так: “исправленное среднее квадратичное отклонение”.