
- •Глава 5. Основные принципы организации и первичной обработки данных эксперимента
- •5.1 Общие положения, эффективность эксперимента
- •5.2 Ошибки измерений при экспериментировании
- •5.3 Элементы теории вероятностей
- •5.3.1 Предмет и основные понятия теории вероятностей
- •5.3.2 Случайные величины и их числовые характеристики
- •Искомая дисперсия:
- •5.3.3 Интегральная функция распределения и числовые характеристики непрерывных случайных величин
- •5.3.4 Нормальное распределение
- •5.3.5 Понятие о системе нескольких случайных величин и их числовых характеристиках
- •5.4 Элементы математической статистики
- •5.4.1 Задача математической статистики
- •5.4.2 Генеральная и выборочная совокупности
- •5.4.3 Статистическое распределение выборки и эмпирическая функция распределения
- •Написать распределение относительных частот.
- •Варианты хi 2 6 10 частоты ni 12 18 30.
- •5.4.4 Полигон и гистограмма
- •5.4.5 Статистические оценки параметров распределения
- •5.4.6 Точность оценки, доверительная вероятность (надёжность). Доверительный интервал
- •5.4.7 Другие характеристики вариационного ряда
- •5.5 Приёмы первичной обработки экспериментальных данных
- •5.5.1 Систематизация данных измерений и нахождение числовых характеристик измеряемых величин
- •5.5.2 Обнаружение грубых ошибок (промахов)
- •5.5.3 Интервальная оценка истинного значения измеряемого параметра
- •5.5.4 Сравнение интервальных оценок измеряемого параметра
- •Результаты измерений плотности прессовок
- •5.6.1 Проверка наличия промахов в выборках
- •5.6.2 Определение интервальных оценок плотности прессовок
- •5.6.3 Проверка гипотезы о статистической значимости различия плотности прессовок, полученных при различных давлениях прессования
- •5.6.4 Проверка нормальности распределения ошибок измерений плотности в выборках
- •Данные для проверки гипотезы о нормальном распределении ошибок измерений плотности прессовок
- •5.7 Вопросы для самоконтроля
Искомая дисперсия:
D(X) = М(Х2) [М(Х)]2 = 13,3 (3,5)2 = 1,05.
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратичное отклонение.
Средним квадратичным отклонением случайной величины X называют квадратный корень из дисперсии:
![]() .
(5.7)
.
(5.7)
Дисперсия имеет размерность, равную квадрату размерности случайной величины, размерность σ(X) совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратичное отклонение, а не дисперсию.
Переход от М(Х) к М(Х2) позволяет лучше учесть влияние на математическое ожидание того или тех возможных значений, которые велики и имеют малую вероятность. Переход к величинам X3, X4 и т. д. позволил бы еще больше “усилить роль” этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).
Начальным моментом порядка k случайной величины X называют математическое ожидание величины Xk:
k=M(Xk). (5.8)
В частности,
1=M(X), (5.9)
2=M(X2). (5.10)
Пользуясь этими моментами, формулу для вычисления дисперсии D(X) = М(Х2) [М(Х)]2 можно записать так:
![]() .
(5.11)
.
(5.11)
Кроме моментов случайной величины X целесообразно рассматривать моменты отклонения [X – M(X)].
Центральным моментом порядка k случайной величины X называют математическое ожидание величины [X – M(X)]k:
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
![]() (5.14)
(5.14)
Моменты более высоких порядков применяются редко.
Моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.
5.3.3 Интегральная функция распределения и числовые характеристики непрерывных случайных величин
Дискретная случайная величина задается перечнем всех ее возможных значений и их вероятностей. Такой способ задания, однако, неприменим для непрерывных случайных величин. С целью задания любых типов случайных величин вводят интегральную функцию распределения.
Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т. е.
F(x) = P(X < x). (5.15)
Геометрически это равенство можно истолковать так: F(x) является вероятностью того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Случайную величину будем называть непрерывной, если ее интегральная функция распределения F(x) непрерывно дифференцируема.
Распространим определения числовых характеристик дискретных величин на величины непрерывные.
Пусть непрерывная случайная величина X задана дифференциальной функцией f(x). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот отрезок на n частичных отрезков длиною х1, х2, ..., хn и выберем в каждом из них произвольную точку хi (i = 1, 2, ..., n). Составим сумму произведений возможных значений хi на вероятности их попадания в интервал хi:
![]() .
(5.16)
.
(5.16)
Перейдя к пределу
при стремлении к нулю длины наибольшего
из частичных отрезков, получим определенный
интеграл
![]() .
(5.17)
.
(5.17)
Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл
 .
(5.18)
.
(5.18)
Если возможные значения принадлежат всей оси х, то
![]() .
(5.19)
.
(5.19)
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения X принадлежат отрезку [а, b], то
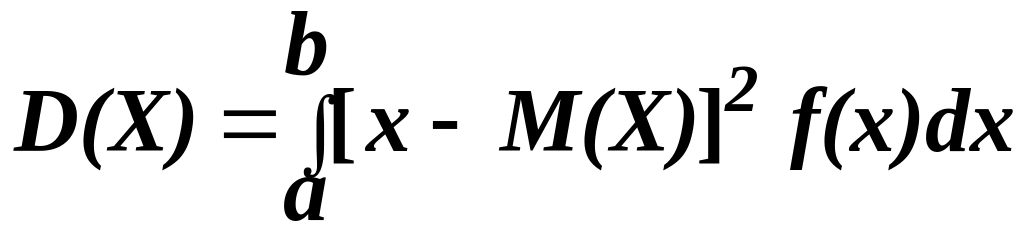 .
(5.20)
.
(5.20)
Если возможные значения принадлежат всей оси х, то
![]() .
(5.21)
.
(5.21)
Среднее квадратичное отклонение непрерывной случайной величины определяется равенством
. (5.22)
