5.4.7 Другие характеристики вариационного ряда

Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда.

Модой М₀ называют варианту, которая имеет наибольшую частоту. Например, для ряда

хi	1	4	7	9
ni	5	1	20	6

мода равна 7.

Медианой m_е называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n = 2k + 1, то m_e = х_{(k + 1)}; при четном n = 2k медиана

. (5.42)

Например, для ряда вариант 2 3 5 6 7 медиана равна 5; для ряда вариант 2 3 5 6 7 9 медиана равна .

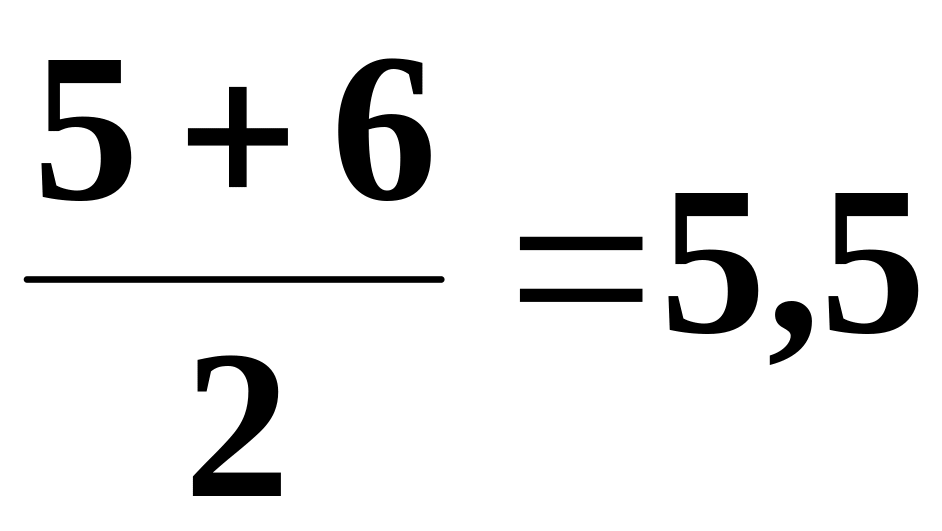Размахом варьирования R называют разность между наибольшей и наименьшей вариантами:

R = x_max – x_min. (5.43)

Например, для ряда варианта 1 3 4 5 6 10

размах R равен 10 – 1 = 9.

Размах является простейшей характеристикой рассеяния вариационного ряда.

Средним абсолютным отклонением f называют среднее арифметическое абсолютных отклонений:

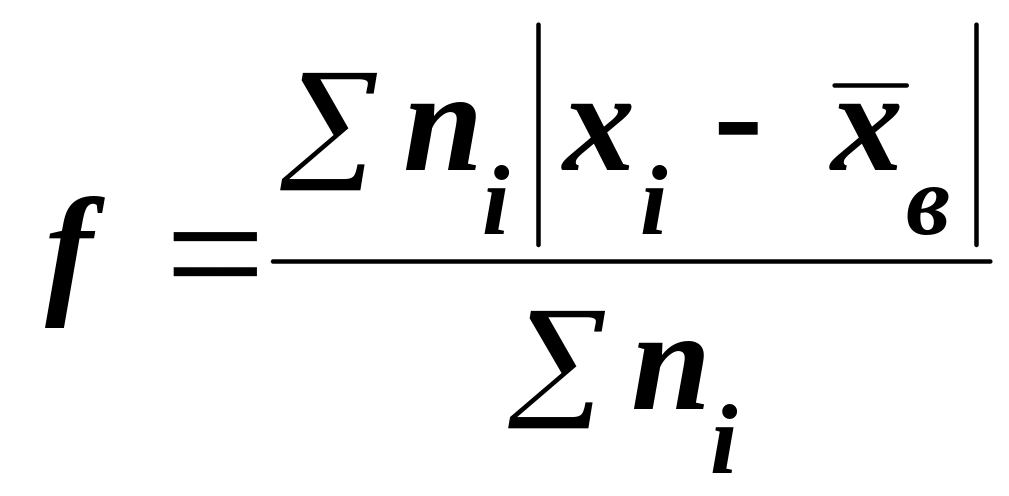. (5.44)

Например, для ряда

хi	1	3	6	16
ni	4	10	5	1

имеем:

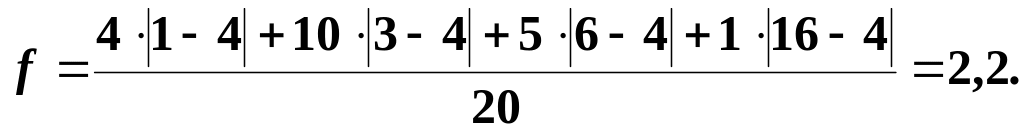
Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.

Коэффициентом вариации называют выраженное в процентах отношение выборочного среднего квадратичного отклонения к выборочной средней:

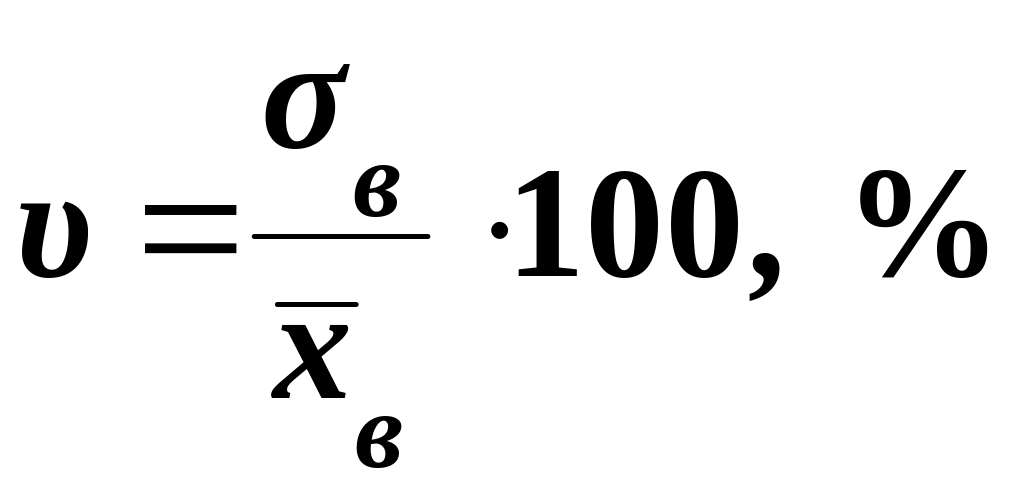. (5.45)

Коэффициент вариации служит для сравнения величин рассеяния двух вариационных рядов: тот из рядов имеет большее рассеяние, у которого коэффициент вариации больше.

Выше предполагалось, что вариационный ряд составлен по данным выборки, поэтому все описанные характеристики называют выборочными. Если вариационный ряд составлен по данным генеральной совокупности, то характеристики называют генеральными.

Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям соответствующих теоретических моментов. В отличие от тео­ретических эмпирические моменты вычисляют по данным наблюдений.

Обычным эмпирическим моментом порядка k называют среднее значение k-x степеней разностей (x_i – c):

, (5.46)

где х_i – наблюдаемая варианта,

n_i – частота варианты,

п = ∑ п_i – объем выборки,

с – произвольное постоянное число (ложный нуль).

Начальным эмпирическим моментом порядка k называют обычный момент порядка k при с = 0.

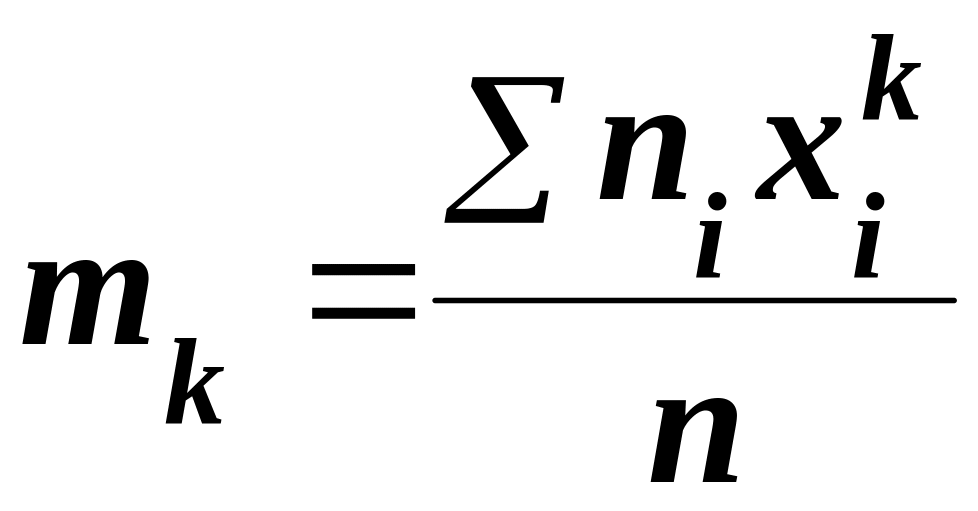. (5.47)

В частности,

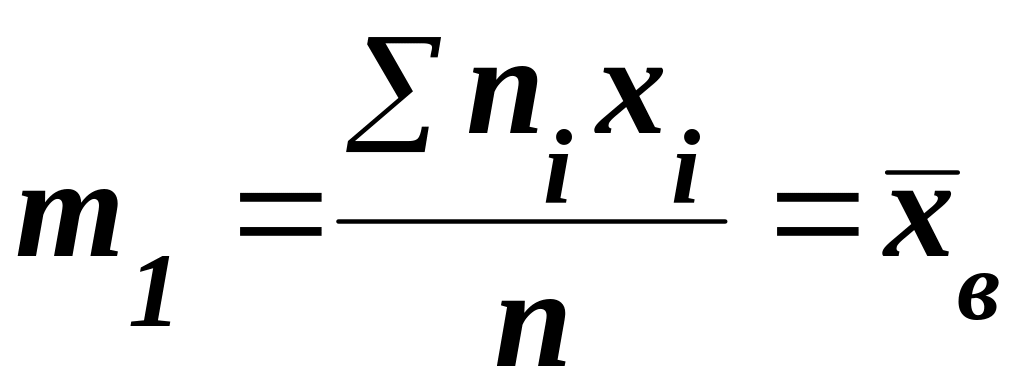, (5.48)

т. е. начальный эмпирический момент первого порядка равен выборочной средней.

Центральным эмпирическим моментом порядка k называют обычный момент порядка k при .

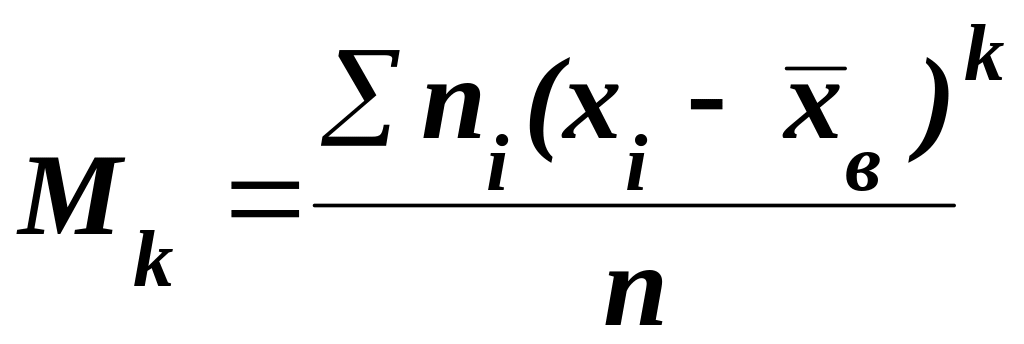. (5.49)

В частности,

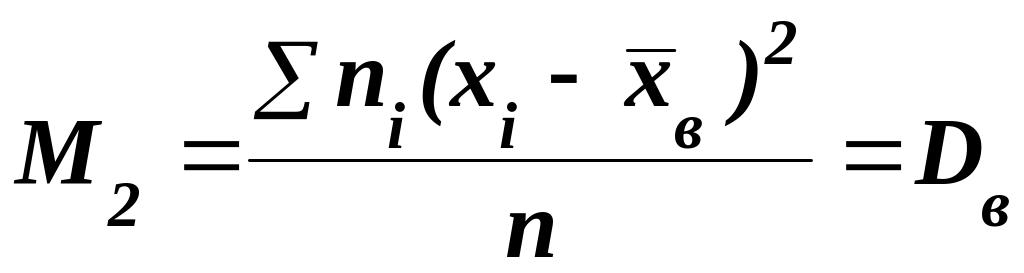, (5.50)

т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.

Легко выразить центральные моменты через обычные:

(5.51)

(5.52)

(5.53)

В случае непрерывного распределения вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности Р попадания значений X в i-й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности.

Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, к числу которых относятся асимметрия и эксцесс. Определения этих характеристик аналогичны определениям асимметрии и эксцесса теоретического распределения.

Асимметрия эмпирического распределения определяется равенством

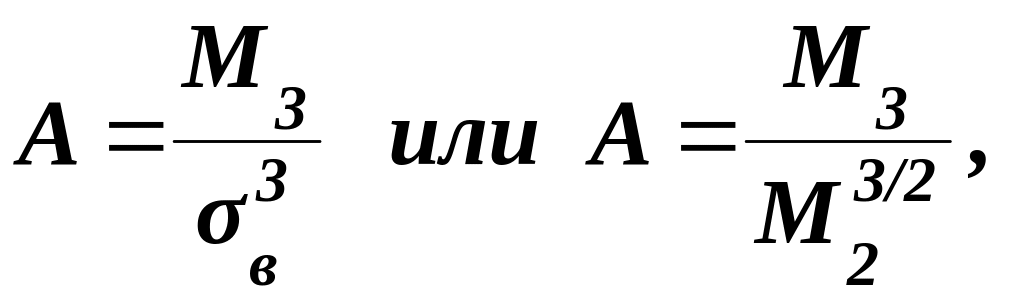(5.54)

где М₂ и M₃ – центральные эмпирические моменты второго и третьего порядка,

– выборочное среднеквадратичное отклонение, т.е.

Эксцесс эмпирического распределения определяется равенством

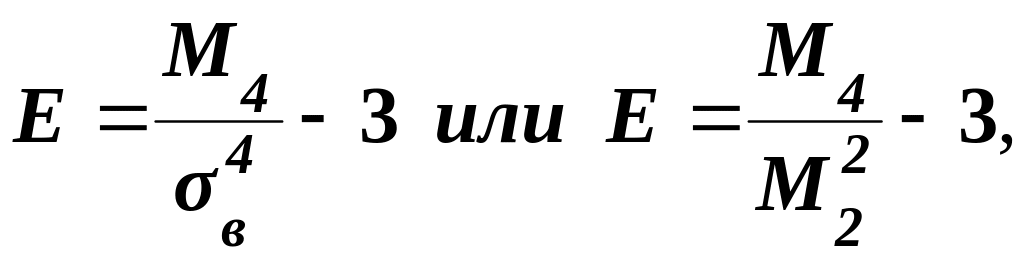(5.55)

где M₄ – центральный эмпирический момент четвертого порядка.