
- •§ 1. Поняття макроекономічної динаміки та критерії її визначення. Економічне зростання та його типи
- •§ 2. Система показників макроекономічної динаміки
- •§ 3. Фактори капіталу, праці і технічного прогресу в динаміці національного продукту. Виробничі функції.
- •§4. Фактори споживання, заощадження, інвестування в динаміці національного продукту. Теорія мультиплікатора Дж.М. Кейнса
- •§ 5. Неокейнсіанські моделі економічного зростання
- •Питання для самоконтролю
- •Література до глави 17
§ 5. Неокейнсіанські моделі економічного зростання
Якщо кейнсіанська теорія пояснювала механізм досягнення сталих темпів економічного зростання за умов спаду і депресивного розвитку економіки, то неокейнсіанські теорії пояснюють шляхи досягнення стійких темпів економічного розвитку та різноманітних варіантів економічної динаміки за різноманітних умов економічної кон’юнктури.
Складовою частиною неокейнсіанських концепцій економічного зростання є теорія акселератора1.
-
Акселератор економічного зростання – це числовий коефіцієнт, який показує взаємозв’язок приросту інвестицій і приросту доходу, що викликав приріст інвестицій.
Акселератор зростання відображається рівнянням:
![]() ,
де
,
де
![]() – коефіцієнт акселерації.
– коефіцієнт акселерації.
На відміну від теорії мультиплікатора інвестицій, у якій мова йшла про автономні (незалежні) від доходу інвестиції, у теорії акселератора мова йде про залежні (похідні) від доходу інвестиції, які отримали назву індуційовані інвестиції.
-
Індуційовані інвестиції – це такі інвестиції, які змінюються в залежності від зміни попиту на товари та послуги в результаті зміни доходу.
Індуційовані інвестиції є функцією від зміни доходу:
![]() .
.
З
індуційованими інвестиціями пов’язаний
принцип акселерації,
зміст якого полягає в тому, що будь-який
приріст або зменшення доходу вимагає
відносно більшого приросту або зменшення
індуційованих інвестицій. Тобто,
![]() змінюється
швидшими темпами, ніж дохід, який викликав
ці зміни.
змінюється
швидшими темпами, ніж дохід, який викликав
ці зміни.
Ефект акселератора полягає в тому, що масштаби інвестування у даному періоді залежать від збільшення національного доходу у попередньому періоді (у році n – 1 в порівнянні із роком n – 2).
У найпростішому вигляді принцип акселерації можна виразити формулою:
![]()
Звідси:
 ,
де
,
де
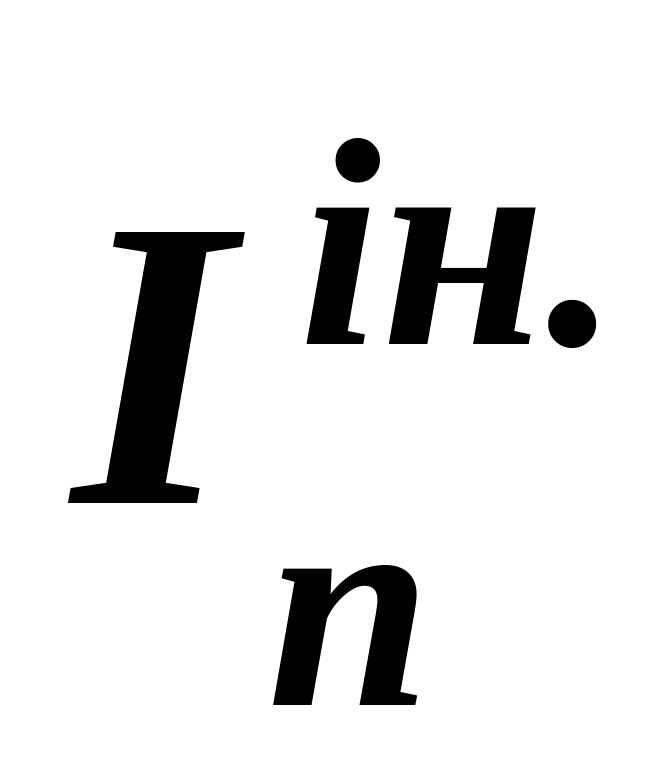 – зростання нових інвестицій
у n-му
році;
– зростання нових інвестицій
у n-му
році;– коефіцієнт акселерації інвестицій;
 – приріст національного
доходу у році n – 1.
– приріст національного
доходу у році n – 1.
Отже, акселератор пов’язує обсяг інвестування даного року зі змінами обсягу доходу попереднього періоду, а мультиплікатор пов’язує нинішнє економічне зростання з інвестиціями минулого періоду.
Ефект акселератора взаємодіє з ефектом мультиплікатора. Саме таку модель економічного зростання розробив англійський економіст Дж. Гікс. Модель Гікса поєднує мультиплікатор і акселератор і відображається рівнянням:
![]() ,
де
,
де
Yn – національний дохід n-го року;
IA – автономні інвестиції;
(1 – S) – MPC;
– коефіцієнт акселератора;
![]() – національний дохід минулого
і позаминулого років.
– національний дохід минулого
і позаминулого років.
Модель Дж. Гікса показує, що зростання інвестицій зумовлює приріст рівня доходу пропорційно мультиплікатору. Зростання доходу зумовлює прискорення темпів зростання попиту на споживчі блага, які, у свою чергу, зумовлюють збільшення інвестицій у засоби виробництва в акселеративній залежності.
Таким чином, згідно з неокейнсіанськими уявленнями, зміни в обсягах виробництва та національного доходу залежать як від автономних інвестицій, що спричиняють ефект мультиплікації, так і від індуційованих (стимульованих) інвестицій, які зумовлюють ефект акселерації.
Одними з перших спроб обгрунтувати довгострокове економічне зростання на основі кейнсіанської макроекономічної теорії були моделі економічного зростання англійського економіста Р. Гаррода та американського економіста О. Домара. Обидва розробляли свої моделі окремо, однак прийшли до аналогічних висновків, тому їх моделі, як правило, розглядаються в комплексі.
Модель
Р. Гаррода досліджує
залежність приросту національного
продукту від норми заощадження й
маржинального коефіцієнту капіталу і
виражається рівнянням:
![]() ,
де
,
де
![]() – норма заощадження
у національному продукті. За умови, що
S=I,
то
буде
виражатися відношенням приросту
інвестицій (ΔI)
до базового рівня національного продукту
(Y0):
– норма заощадження
у національному продукті. За умови, що
S=I,
то
буде
виражатися відношенням приросту
інвестицій (ΔI)
до базового рівня національного продукту
(Y0):
![]() .
.
C
–
капітальний (маржинальний)
коефіцієнт, який показує ефективність
витрат капіталу на
виробництво одиниці продукту:
![]() .
.
g
– темп
економічного приросту:
![]() .
.
Відповідно базове
рівняння набуває такого вигляду:
![]() .
Звідси,
.
Звідси,
![]() .
.
Це рівняння відображає стан економічної рівноваги за умови, коли темп приросту інвестицій дорівнює темпу приросту капіталомісткості (маржинальному коефіцієнту).
Темп економічного
приросту визначається рівнянням:
 .
.
Це рівняння показує, що темп економічного зростання прямо пропорційний обсягу заощаджень (нагромадженню капіталу для інвестицій) і обернено пропорційний маржинальному коефіцієнту (капіталомісткості національного продукту). Для прискорення економічного зростання слід або збільшити норму нагромадження, або зменшити капіталомісткість продукту. Умовою динамічної ріноваги (коли I =S) при постійній нормі нагромадження і постійній капіталомісткості національного продукту є стійкі темпи економічного зростання. Однак, динамічна рівновага у цій моделі виявляється мінливою, тому Гаррод аналізує досягнення рівноваги при різних темпах зростання. У моделі вводяться поняття “гарантований темп зростання”, “природний темп зростання” і “фактичний темп зростання”.
Гарантований
темп зростання (gn)
визначається рівнянням:
![]() ,
де CR
– капіталомісткість за мінімально
можливої норми нагромадження. Це
стабільний і сталий темп, який забезпечує
динамічну рівновагу та повне використання
усіх виробничих ресурсів.
,
де CR
– капіталомісткість за мінімально
можливої норми нагромадження. Це
стабільний і сталий темп, який забезпечує
динамічну рівновагу та повне використання
усіх виробничих ресурсів.
Природний
темп зростання (gn)
– це максимально можливий темп
економічного розвитку при максимально
можливій капіталомісткості та нормі
нагромадження (![]() ):
):![]() .
.
Фактичний темп
зростання відображається рівнянням:
![]() .
.
Аналізуючи причини відхилення від умов гарантованого темпу зростання, Гаррод прийшов до висновку, що у ринковій економічній системі відсутні автоматичні стабілізатори рівноваги. Ця обставина лежить в основі обгрунтування необхідності державного втручання в економіку.
Бажаним станом для економіки є ситуація, коли gw = gn = g, тобто, коли всі три темпи економічного зростання урівноважуються. За такого оптимального співвідношення маржинальний коефіцієнт буде найнижчим, а економічний потенціал суспільства використовуватиметься найефективніше.
Модель економічного зростання Овсія Домара також визначає залежність зростання доходу (ΔY) від граничної схильності до заощадження (S) і середньої продуктивності інвестицій (c). Модель виражається рівнянням:
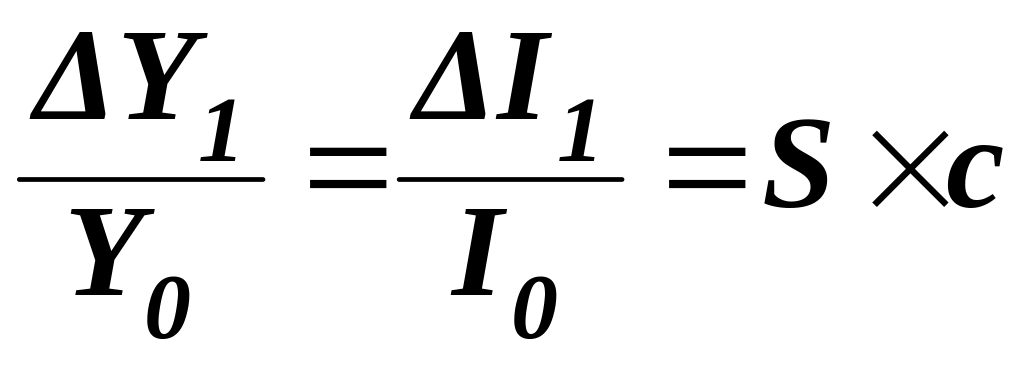 .
.
Тобто динамічна
рівновага економічного зростання
можлива за умови, коли темпи національного
доходу і інвестицій зростатимуть на
величину, що дорівнює добуткові граничної
схильності до заощаджень (S)
і середній продуктивності інвестицій
(c):
![]() .
.
Отже, О. Домар практично прийшов до тих же висновків, що і Р. Гаррод. Тому їх моделі розглядаються в єдиній системі, яка отримала назву моделі економічного зростання Гаррода–Домара. Ця модель показує, що динамічна рівновага у довгостроковому періоді забезпечується за такого співвідношення факторів зростання, коли встановлюється рівність приросту попиту і пропозиції. Таку рівність можна забезпечити шляхом визначення оптимальної норми нагромадження і необхідного рівня маржинального коефіцієнт (граничної капіталомісткості продукту).
