Моделирование.
Требования к системам управления каналами:
=0.1c;
%..
Стабилизация обеспечивается пропорциональным регулятором (алгоритмом управления) вида
,
где
–
матрица-строка коэффициентов обратной
связи.
После подстановки алгоритма получаем уравнение состояния замкнутой системы
,
где
.
Соответствующий характеристический
полином принимает вид
.
В
соответствии с методом модального
управления устойчивость положения
равновесия синтезируемой системы и
заданные динамические показатели
качества
и
достигаются за счет назначения корней
характеристического уравнения
,
что в свою очередь обеспечивается
соответствующим выбором коэффициентов
обратных связей
.
По
заданным качественным показателям
с и
с использованием метода стандартных
переходных функций найдем корни
характеристического уравнения замкнутой
системы
и коэффициенты желаемого характеристического
уравнения
.
Выберем желаемую переходную характеристику,
соответствующую биноминальному полиному
второго порядка
.
Нормированное
время переходного процесса для
с, перерегулирование
%.
Минимально допустимый радиус распределения
корней
.
Коэффициенты
полинома
,
и его корень
.
Коэффициенты
матрицы обратной связи
,
соответствующей канонической (управляемой)
форме объекта, рассчитываются как
Для обратного перехода (от канонической формы к исходному представлению системы) используется преобразование
,
где
–
матрица преобразования (подобия),
рассчитываемая как
,
а
–
матрица управляемости канонической
модели ОУ.
.
1) Для первого канала:
2) Для первого канала:
3) Для третьего канала:
Отработка первым каналом постоянного воздействия при
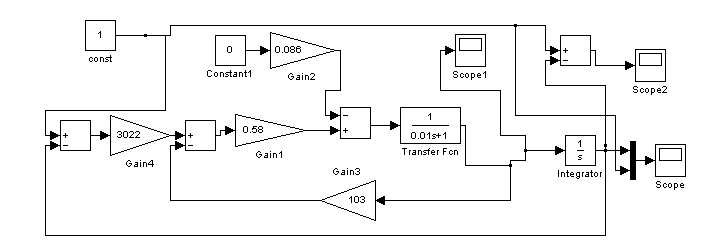
Рисунок 7-Схема моделирования первого канала
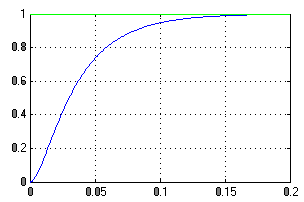
Рисунок 8-Переходной процесс в системе
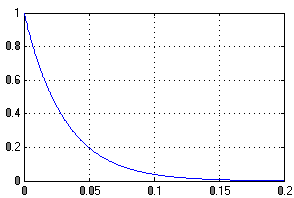
Рисунок 9-Ошибка
Ступенчатое воздействие система отрабатывает без ошибок.
Перерегулирование - %;
Время
переходного процесса -
0,1
с.
Отработка первым каналом линейно нарастающего воздействия при
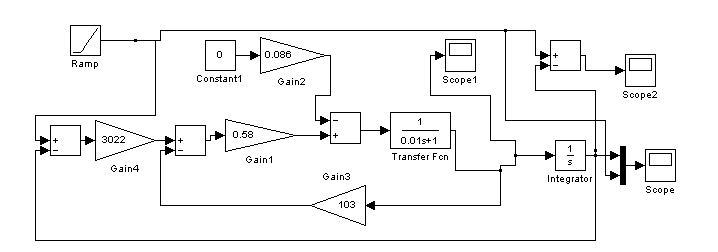
Рисунок 10 -Схема моделирования первого канала
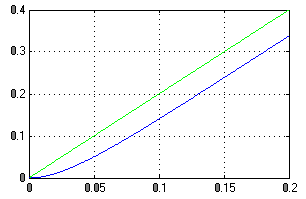
Рисунок 11 - Переходной процесс в системе
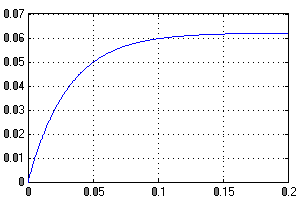
Рисунок 12 - Ошибка
Линейно-нарастающее воздействие система отрабатывает с постоянной установившейся ошибкой (комбинированное управление позволяет свести ошибку к нулю).
Отработка первым каналом воздействия с постоянным ускорением при
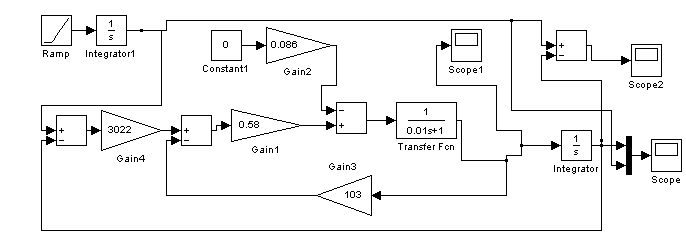
Рисунок 13 -Схема моделирования первого канала
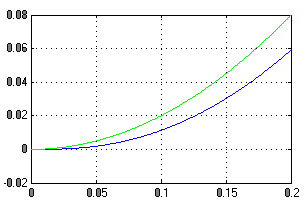
Рисунок 14 - Переходной процесс в системе
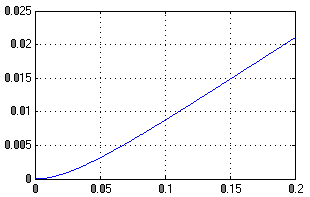
Рисунок 15 - Ошибка
Воздействие с постоянным ускорением система отрабатывает с нарастающей ошибкой, так как система обладает астатизмом первого порядка по отношению к задающему воздействию.
Отработка первым каналом постоянного воздействия при
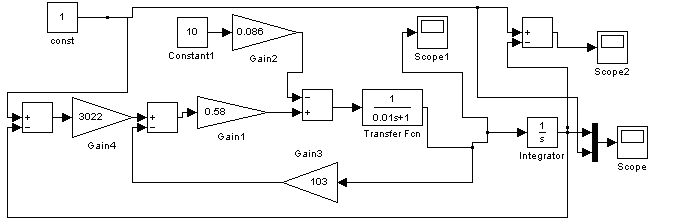
Рисунок 16 -Схема моделирования первого канала
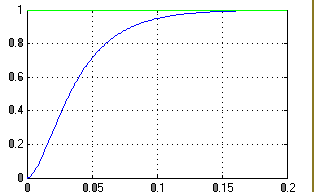
Рисунок 17 - Переходной процесс в системе
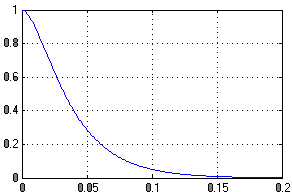
Рисунок 18 - Ошибка
Отработка первым каналом линейно нарастающего воздействия при
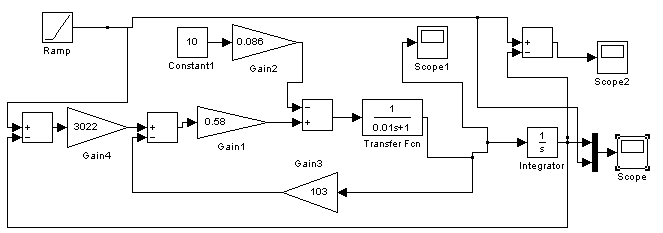
Рисунок 19-Схема моделирования первого канала
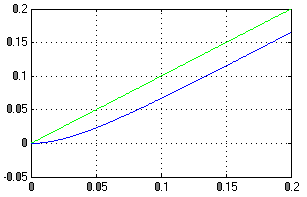
Рисунок 20 -Переходной процесс в системе
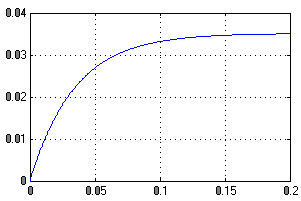
Рисунок 21 - Ошибка