Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики

Кафедра систем управления и информатики

Расчетно-графическая работа

по курсу " Робототехнические системы и комплексы".

Выполнил: студент гр. 5146

Багаутдинов Е.

Преподаватель:

Котельников Ю.П.

Санкт-Петербург

2010 г.

Техническое задание.

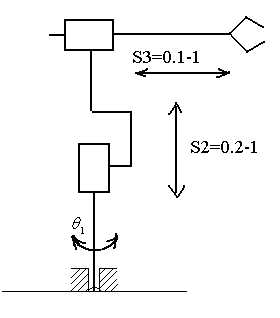
Рисунок 1-Техическое задание.

Решение прямой и обратной задач кинематики.

Основным вопросом при рассмотрении манипулирования с использованием роботов является способность поместить объект управления (схват манипулятора) в определенную точку с требуемой ориентацией в заданное время.

Прямая задача кинематики.

Определение - вектора, определяющего положение схвата манипулятора, при известном векторе параметров :

,

.

Обратная задача кинематики.

Определение параметров звеньев манипулятора, если известен вектор - радиус вектор схвата.

Для решения прямой и обратной задач необходимо определенным образом осуществлять выбор систем координат.

Выбор систем координат.

Манипулятор представляет собой систему материальных тел (звеньев), образующих разомкнутую кинематическую цепь. Звенья этой цепи образуют поступательная кинематическая пары 5-го класса и вращательная кинематическая пара пятого класса.

Для того чтобы описать положение -го звена в системе , свяжем с этим звеном декартову систему координат . В качестве основной системы обычно выбирается система , связанная со стойкой манипулятора. Ось направим вдоль первого звена манипулятора. В качестве оси выбирается перпендикуляр к оси , а направление задается так, чтобы система координат была правой. При таком выборе систем координат каждая - тая система координат связана с - тым звеном манипулятора.

Выбор систем координат

Система координат связывается со схватом манипулятора. Обозначим угол поворота - го звена относительно - го через , а величину относительного поступательного перемещения через . Величины и соответствуют паре с номером . Совокупность величин и однозначно определяют положение механизма в пространстве. Эти величины названы обобщенными координатами механизма и обозначаются вектором , причем ,

где - для вращательной пары, - для поступательной пары.

Система координат.

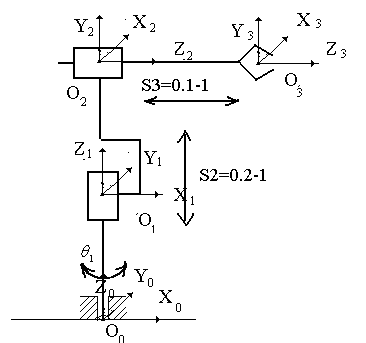
Рисунок 2-Система координат.

Из параметров и один является переменным и совпадает с обобщенной координатой, соответствующей - ой кинематической паре, другой параметр постоянен: для пары вращения , для пары поступательного движения . Общий случай матрицы преобразования:

.

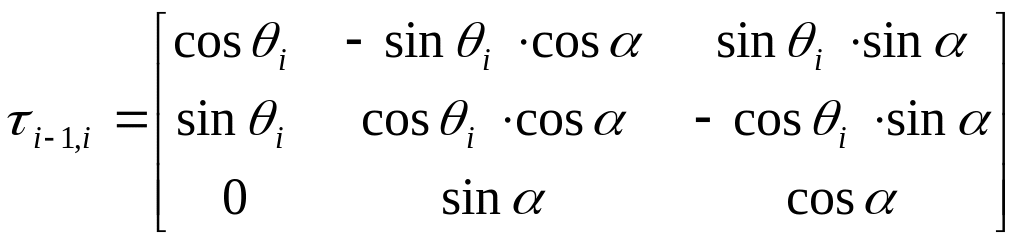Опишем связь между введенными выше системами координат. Нулевая система может быть совмещена с первой системой посредством следующих последовательно выполняемых операций:

(а) поворот на угол ₁ вокруг оси Z₀ до тех пор, пока оси x₀ и x₁ не станут параллельными;

(б) перенос на величину S₁ вдоль оси z₀ до тех пор, пока оси X₀ и х₁ не совместятся;

(в) перенос на величину а₁ вдоль оси x₁, до совпаде­ния начала координат O₀ с началом координат O₁;

(г) поворот на угол ₁ относительно оси x₀ до совме­щения всех координатных осей.

2.1 Решение прямой задачи кинематики. Формулы перехода

Матрица преобразования координат

;

1. Между системами : .

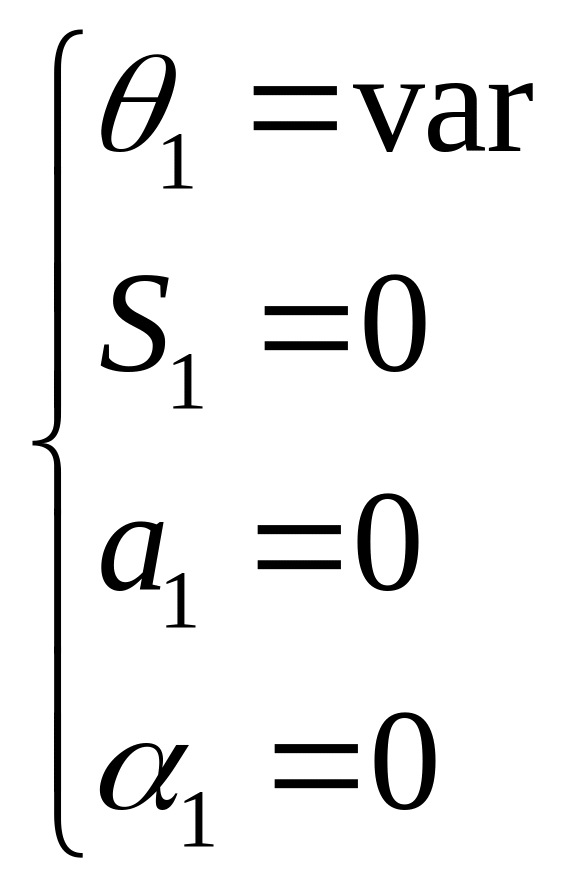Из рисунка видно, что .

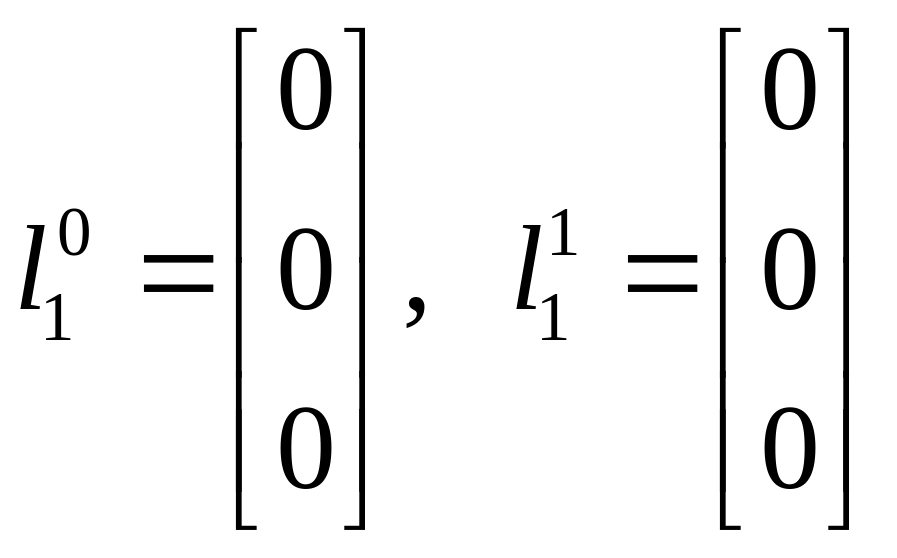Матрица преобразования координат:

, , .

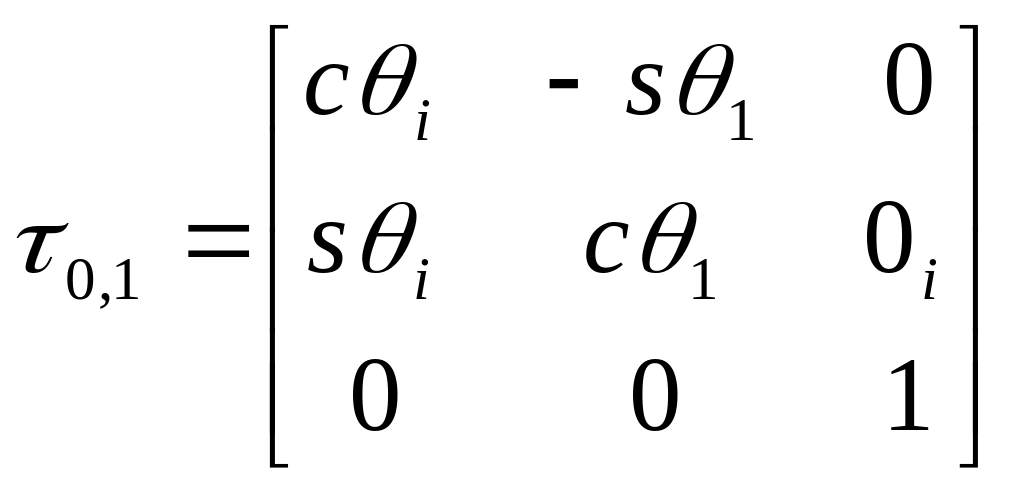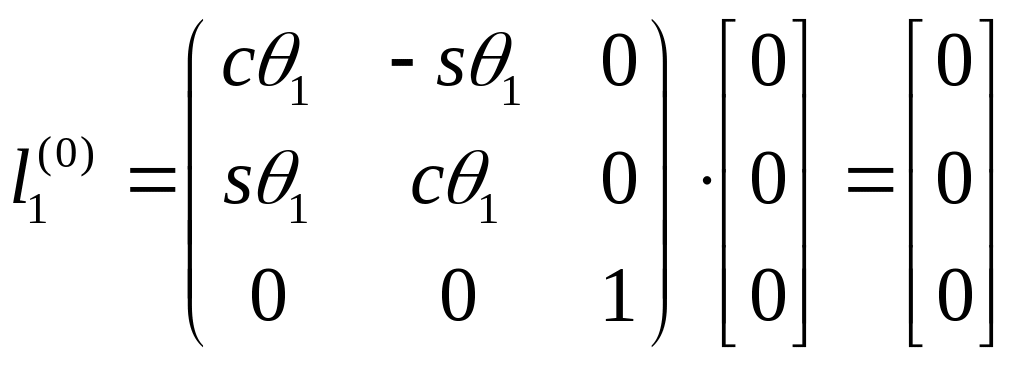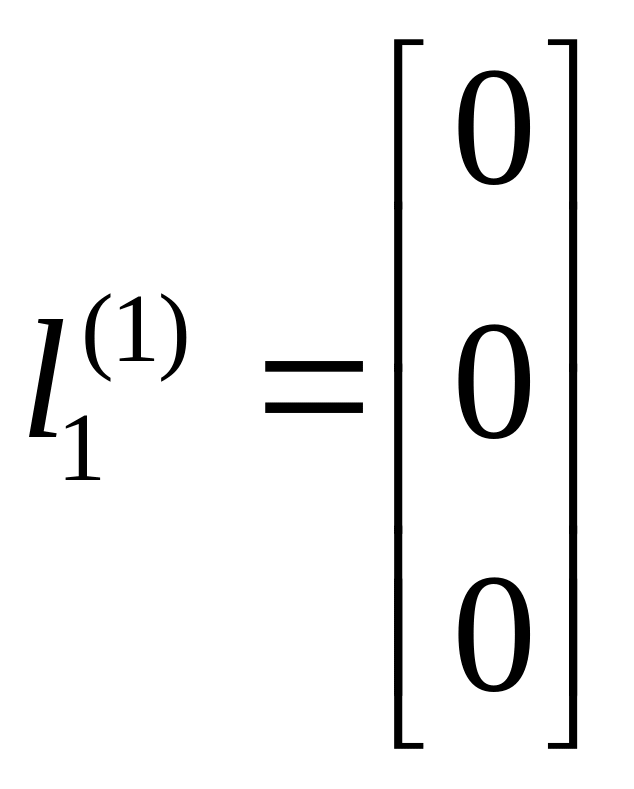2. Между системами : .

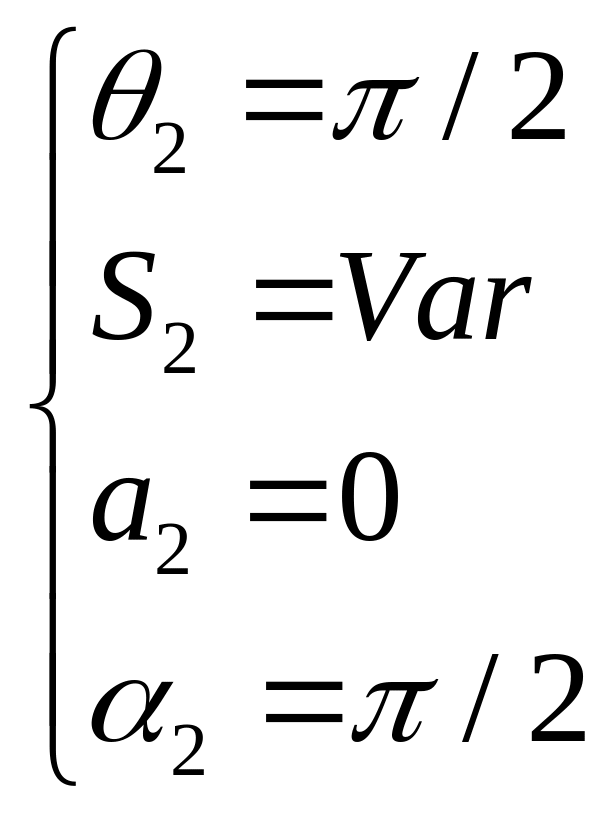Из рисунка видно, что .

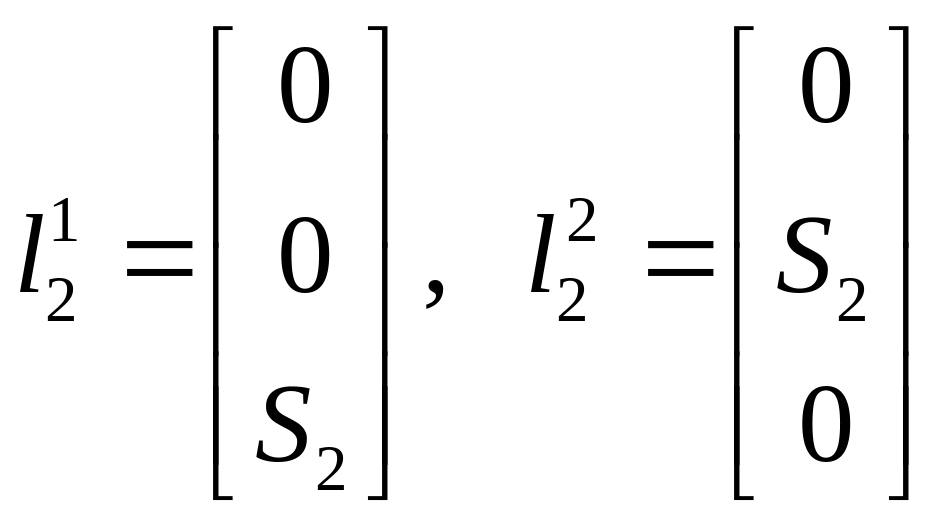Матрица преобразования координат:

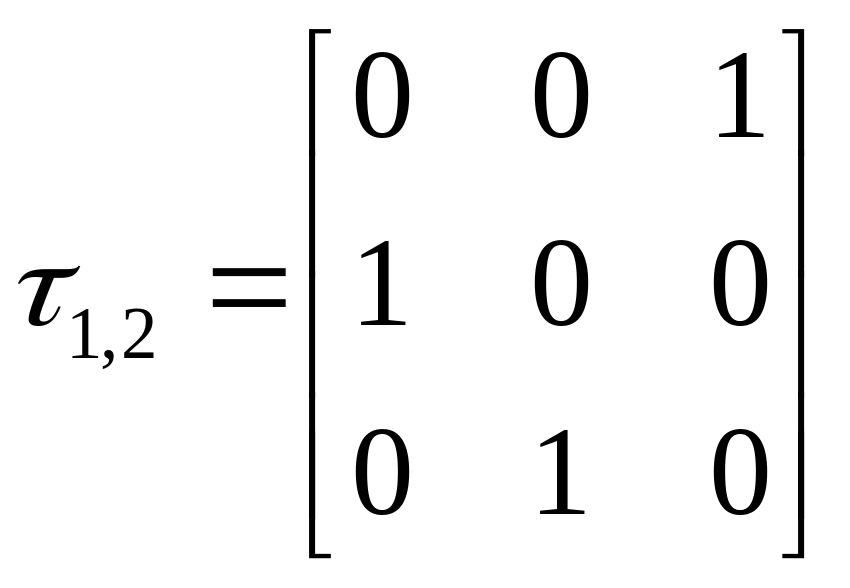, l₂¹ = ₁₂  l₂² = .

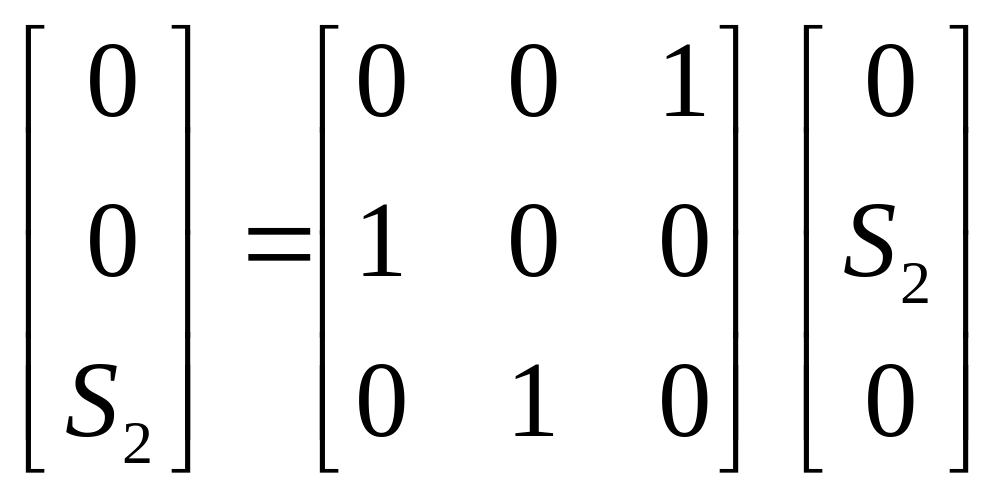3. Между системами : .

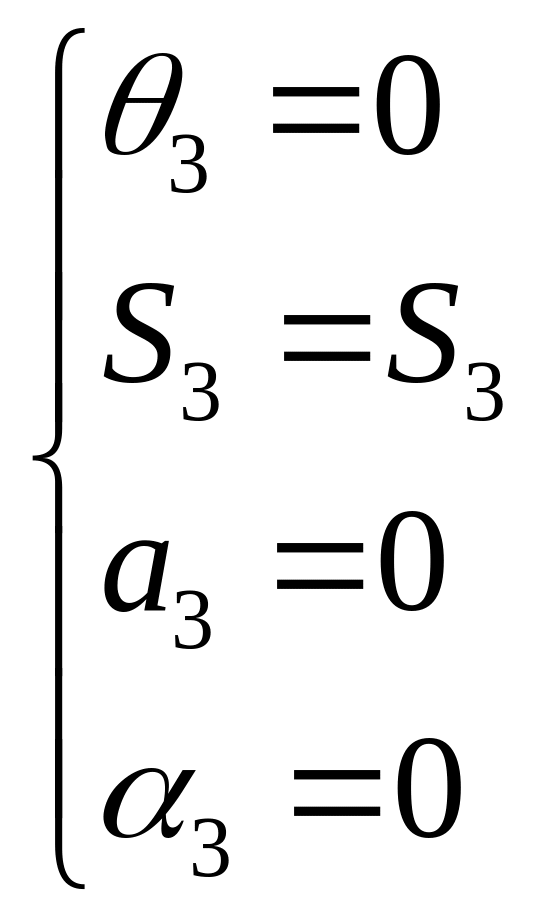Из рисунка видно, что .

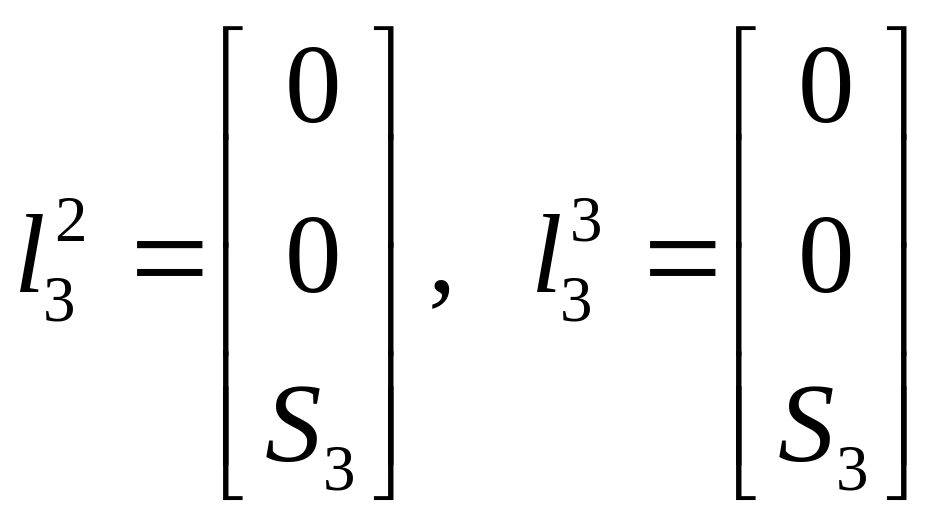Матрица преобразования координат:

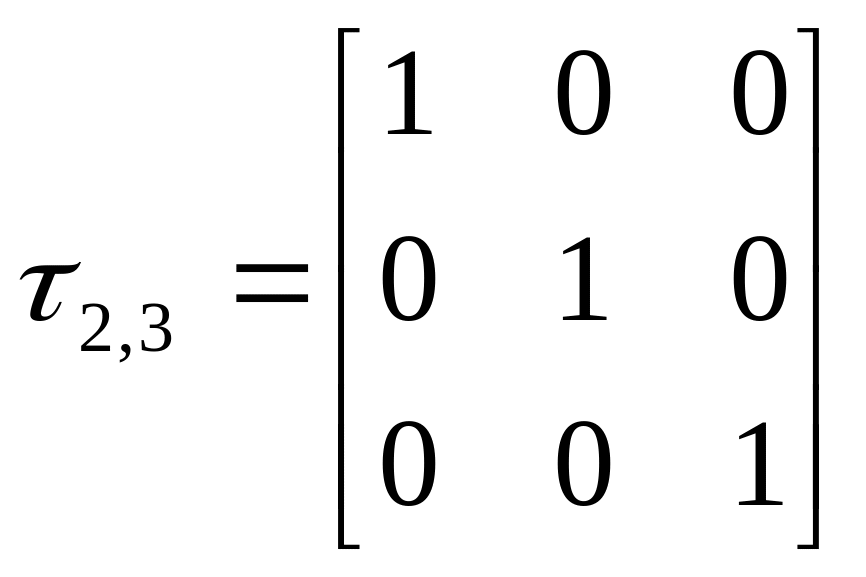, l₃² = ₂₃  l₃³ = .

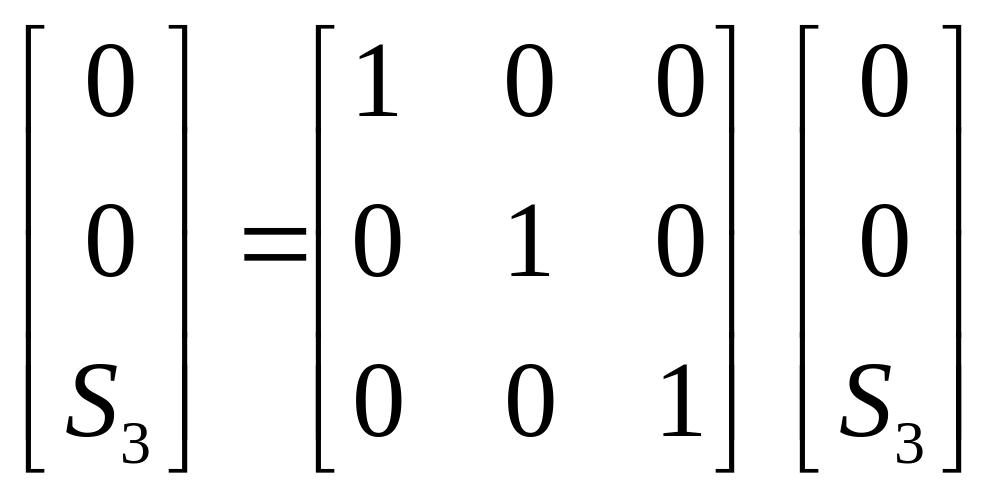Вектор, определяющий положение схвата манипулятора:

.

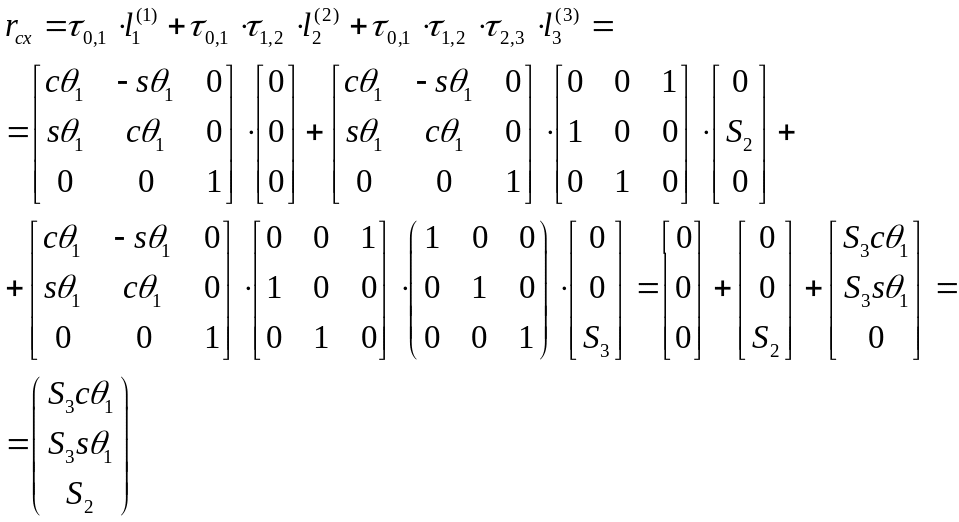
Проверка: 1) Повернем робот так, что =0, , тогда

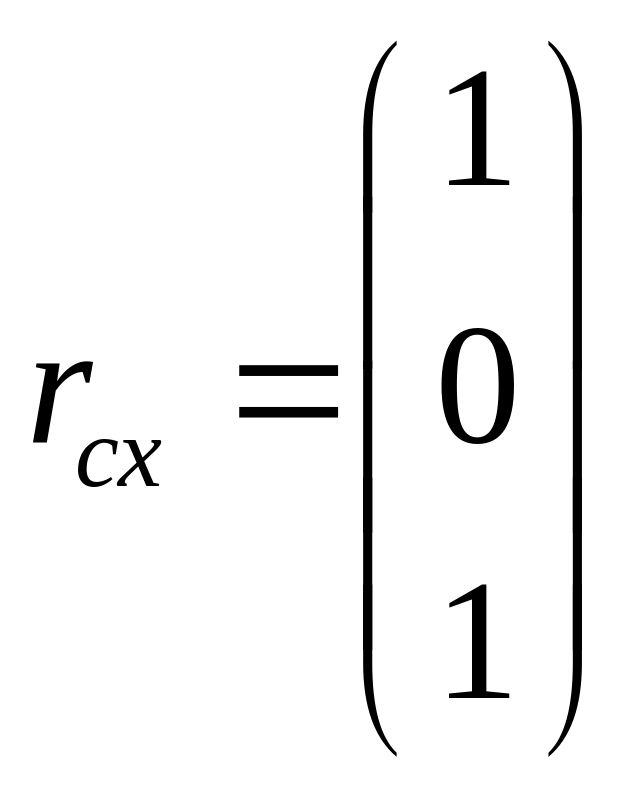
Рисунок 3 – Положение манипулятора

2) Повернем робот так, что =90, , тогда 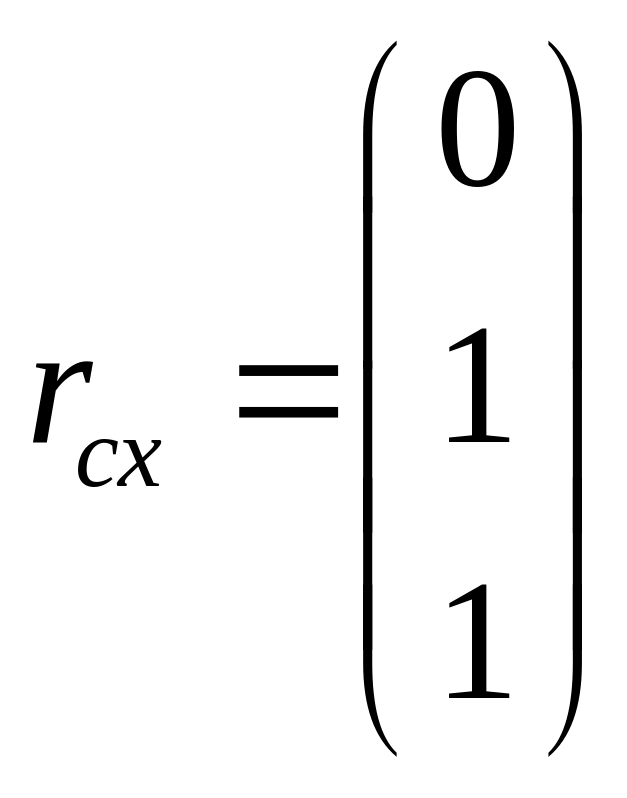, то есть схват манипулятора будет смотреть в сторону доски-и соответственно будет иметь 0 координату по х, по y=1,z=1.