2.11. Метод –поиска

Алгоритм данного метода построен во-многом аналогично алгоритму метода статистических испытаний. Основное отличие со­стоит в том, что в данном случае изображающая точка выбирается не случайным образом, а из так называемых –последовательностей чисел, построенных в области изменения нормирован­ных параметров оптимизации. Указанные последовательности являются наиболее равномерно распределен­ными среди всех известных в настоящее время последовательностей [4]. Значения параметров оптимизации в k-й точке поиска определяются соотношением:

,

(2.16)

где

, ,

(2.17)

– значение базового числа –последовательности, [z] – целая часть, {z} – дробная часть числа.

Точность определения экстремума функции цели методом –поиска задаётся объёмом  по (2.13), а усло­вием окончания поиска является аналогично методу статистических испытаний просмотр такого количества точек N_p, которое обеспечивает гарантированное попадание хотя бы одной точки последовательности в каждый n-мерный объём  области поиска, и вычисляется следующим образом:

.

(2.18)

2.12. Характеристика оптимизации электромеханических устройств и систем методами направленного поиска. Метод градиента

В курсе лекций изучаются и исследуются методы и алгоритмы направленного поиска оптимальных проектных решений: градиентного, случайного и покоординатного поиска и рассматривается их применение при параметрической оптими­зации ГД.

Для решения задач параметрической оптимизации ЭМУС находят широкое применение методы направленного поиска.

В отличие от пассивного поиска для этих методов характерно:

1. целенаправ­ленное движение в области изменения параметров оптимизации от худшего вари­анта к лучшему;

2. при этом направление поиска последующей точки определяется местоположением предыдущей, т. е. конкретный вариант объекта проектирования, в частности при проектировании ЭМУС – вариант, например, гироскопического электродвигателя системы управления летательным аппаратом или генератора системы электроснабжения, определяется, кроме всего прочего, предыдущим вариантом.

Методы направленного поиска позволяют суще­ственно уменьшить затраты на определение экстремума функции цели по сравне­нию с методами пассивного поиска.

В то же время для методов направленного поиска характерно:

1. более сложные алгоритмы поиска по сравне­нию с методами пассивного поиска;

2. они поз­воляют определить приближение лишь к локальному экстремуму функции цели в допустимой области изменения параметров оптимизации;

3. процесс поиска ими существенно затрудняется при наличии ограничений.

Необходимо более подробно рассмотреть алгоритм этих методов.

Метод градиента

В основе метода градиента, как и других градиентных методов, лежит организация движения изображающей точки в направлении градиента (антиградиента) функции цели Q, который определяется соотношением

,

(2.19)

где – единичный вектор по оси x_i.

По определению градиент это вектор направление, которого совпадает с направлением, в котором функция возрастает с наибольшей скоростью, а модуль определяется совокупностью частных производных по переменным.

Алгоритм метода градиента укрупнённо состоит из следующих основных этапов:

1. Выбирается точка начала поиска. В отличие от методов пассивного поиска в этом случае поиск должен начинаться из некоторой точки в области допустимых значений па­раметров S. Необходимость выполнения этого требования объяс­няется тем, что вычисление градиента Q может оказаться не­возможным вне области S, так как нарушения некоторых ограни­чений приводят к изменению математических моделей объекта или отдельных параметров. Для математического описания ЭМУС, в том числе и для ГД, характерно отсутствие явновыраженных зависимостей функции цели от параметров, поскольку функ­циональные зави­симости для показателей объекта проектирования

(2.20)

имеют неявновы­раженный характер. Поэтому на практике используется численный ме­тод определения градиента gradQ, в соответствии с которым даются малые приращения x_i каждому нормированному параметру в отдельности и в резуль­тате расчётов определяются соответствующие приращения функции цели Q_i. Тогда выражение (2.19) преобразуется к виду

(2.21)

то есть частные производные заменяются отношениями приращений. Понятно, что число обращений к модели объекта проектирования возрастает с увели­чением размерности области поиска n.

2. Нормируются изменяемые параметры. Поиск экстремума функции цели в области нормированных параметров позволяет, во-первых, преодолеть разнородность параметров оптимизации, во-вторых, от­строиться от несопоставимости пределов их изменения. Нормирование параметров осуществляется по соотношению

(2.22)

3. Осуществляется поиск внутри допустимой области изменения параметров с рабочим шагом h. Для совершения очередного k-го шага в направлении гради­ента Q параметры объекта проектирования (координаты изображающей точки) преобразуются следующим образом:

.

(2.23)

где – коэффициент пропорциональности, определяющий величину рабочего шага по i-му параметру.

4. На каждом рабочем проверяются ограничения и наличие улучшения значение функции цели. Если при выполнении очередного шага нарушаются ограничения или не уда­ется улучшить значение функции цели, первоначально заданная величина рабо­чего шага уменьшается, как правило, в 2 раза, и действия по определению координат изображающей точки, проверке ограничений и определению зна­чения Q повторяются снова.

5. Деление рабочего шага продолжается до тех пор, пока не будет достигнуто улучшения значения функции цели или не будет выполнено условие окончания поиска. Это условие состоит в следую­щем: если в выбранном в некоторой точке 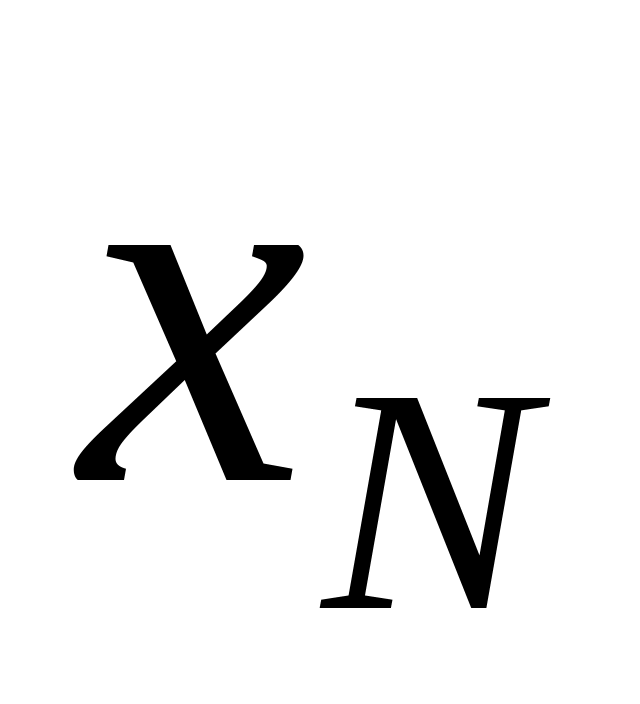направлении на удаётся выполнить рабочий шаг, дающий улучшение функции цели и по значению превышающий некоторое положительное заранее задан­ное малое число , соответствующее, нап­ример, нормированному значению отрезка разбиения 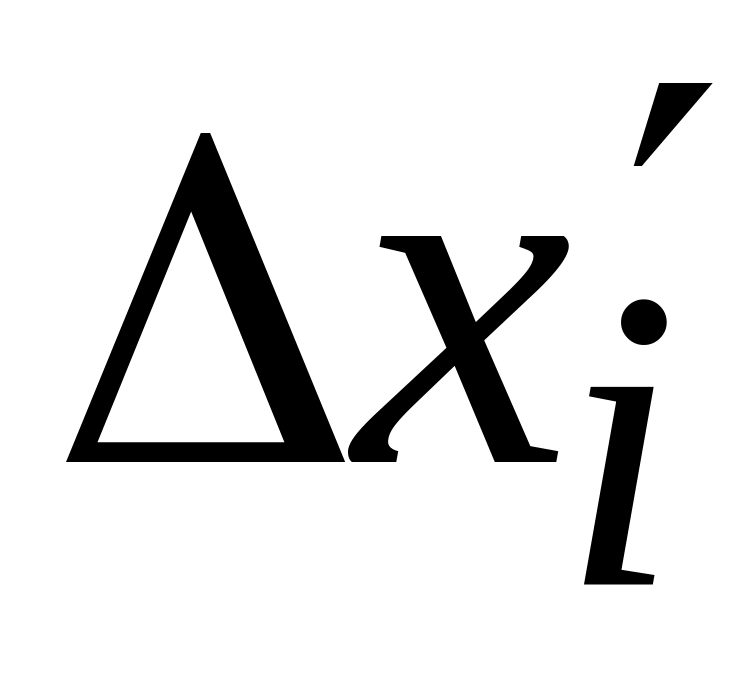в методах пассивного поиска, то поиск считается закончен­ным. Минимальная величина рабочего шага  будет в данном слу­чае характеризовать точность приближения к точке, соответствую­щей экстремуму Q в пространстве параметров. Таким образом, условие окончания поиска следующее:

,

(2.24)

В случае действия ограничений поиск заканчивается при первом выходе на границу области допустимых значений параметров S.

Особенности реализации алгоритма метода градиента состоят в следующем:

1. в организации численного вычисления градиента Q, для чего надо n раз определить значение приращения Q при изменениях параметров x_i, i=1,2,…,n.

2. точность приближения к локальному экстремуму харак­теризуется объёмом -окрестности, которая представляет собой п-мерный параллелепипед, и определяется следующим образом:

,

(2.25)
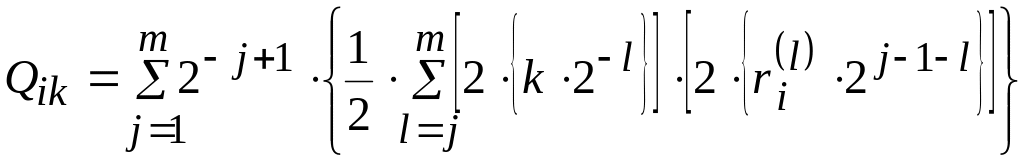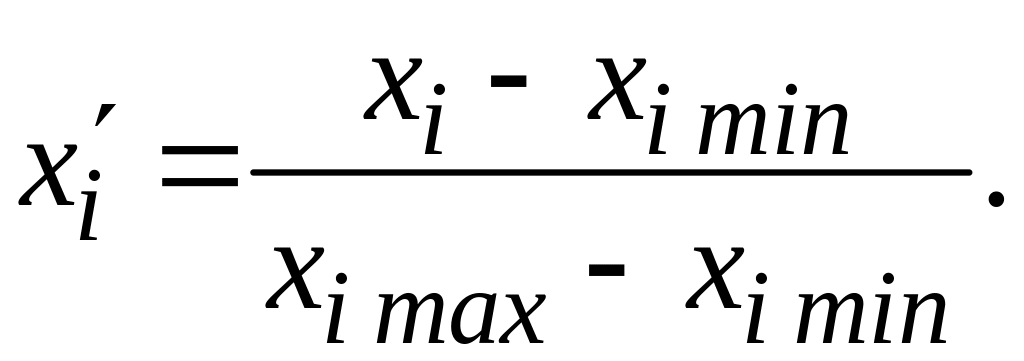
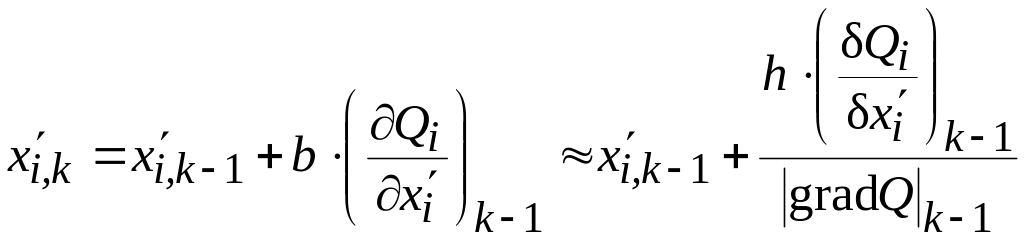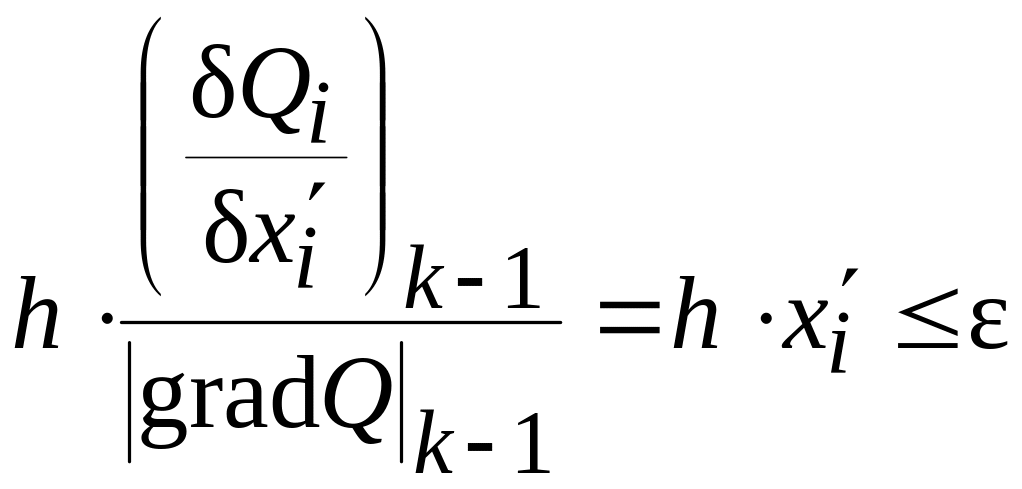