3.2. Перспектива прямой линии
Пример 3.1
Через точку A, заданную своей перспективой и перспективой основания, провести прямую m, перпендикулярную картине, и прямую n, параллельную основанию картины.
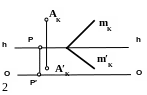
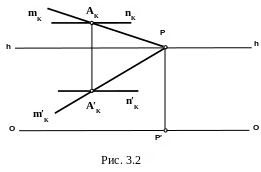
Решение (рис. 3.2)
Если прямая проходит через точку, то перспектива основания прямой проходит через перспективу основания точки и перспектива прямой проходит через перспективу точки. И прямая m и прямая n являются прямыми частного положения.
Прямая m расположена перпендикулярно картине, следовательно, перспектива бесконечно удаленной точки прямой m совпадает с перспективой основания прямой m и находится в главной точке картины.
Прямая n параллельна основанию картины, следовательно, и перспектива прямой n и перспектива основания прямой n расположены параллельно линии горизонта hh.
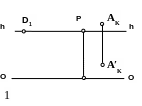
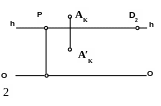
Задание 3.3
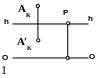
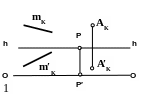
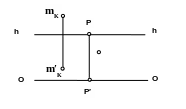
Через точку А провести прямую m перпендикулярно картине.
P′ |
P′ |
P′ |
Задание 3.4
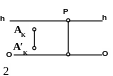
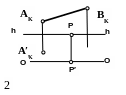
Построить перспективу прямой АВ, параллельной предметной плоскости.
|
|
Задание 3.5
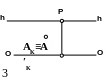
Построить перспективу прямой АВ. АВ параллельна картине и предметной плоскости.
Задание 3.6
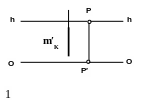
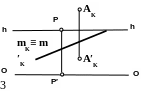
Построить перспективу прямой m, перпендикулярной картине.
Задание 3.7
Построить перспективу основания прямой AB. AB // К.
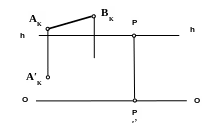
Задание 3.8
Построить перспективу основания прямой m, идущей в точку зрения S.
Задание 3.9
Построить перспективу прямой m, идущей в точку стояния.
|
|
Задание 3.10
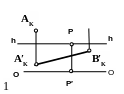
Построить перспективу прямой АВ, параллельной предметной плоскости и идущей под углом 45о к картине.
P′ |
P′ |
3.3. Взаимное положение прямых
Пример 3.2
Через точку A провести прямую n параллельно прямой m.
Решение (рис. 3.3)
Положение прямой в пространстве определяется положением двух ее точек. Таким образом, для построения прямой n необходимо определить еще одну точку, принадлежащую прямой n, например ее бесконечно удаленную точку. Поскольку прямая n параллельна прямой m, то у них общая бесконечно удаленная точка, именуемая точкой схода. Для построения бесконечно удаленной точки прямой m, надо перспективу основания прямой m продлить до пересечения с линией горизонта hh, получив перспективу основания бесконечно удаленной точки, и на пересечении линии проекционной связи и перспективы прямой m построить перспективу бесконечно удаленной точки прямой m – точку F (F'K, F'K). Она же будет бесконечно удаленной точкой прямой n (NK , N'K).
Задание 3.11
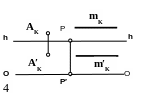
Через точку А провести прямую АВ параллельно прямой m.
|
|
|
|
|
|
Задание 3.12
Построить перспективу прямой CE, пересекающей прямую АВ и параллельной предметной плоскости.
|
2 |
Задание 3.13
Через точку A провести горизонтальные прямые: g – направленную в точку стояния наблюдателя; l – расположенную перпендикулярно картине; m – идущую параллельно картине; n – расположенную под углом 450 к картине. Через точку В провести прямые e, f, J, I параллельно дорожкам g, l, m, n, проведенным через точку А.
