2.2.1. Следы прямой

Пример 2.4

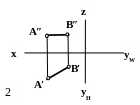
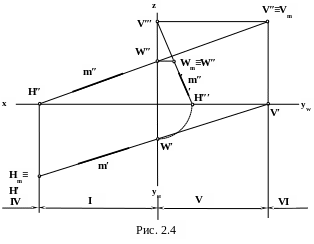
Построить следы прямой m и определить, через какие октанты проходит прямая.

Решение (рис. 2.4)

1. Для построения горизонтального следа H_m прямой нужно фронтальную проекцию прямой продлить до пересечения с осью x в точке H″_m, которая является фронтальной проекцией горизонтального следа прямой m. Горизонтальная проекция горизонтального следа, точка H′_m, которая совпадает с самим горизонтальным следом H_m, будет находиться на линии проекционной связи и на горизонтальной проекции прямой m′. Профильная проекция горизонтального следа H′″ находится в точке пересечения профильной проекции прямой m с осью y.

2. Для построения фронтального следа V_m прямой нужно горизонтальную проекцию прямой продлить до пересечения с осью x в точке V′_m, которая является горизонтальной проекцией фронтального следа прямой m. Фронтальная проекция фронтального следа, точка V″_m, которая совпадает с самим фронтальным следом V_m, будет находиться на линии проекционной связи и на фронтальной проекции прямой m″. Профильная проекция фронтального следа V′″ находится в точке пересечения профильной проекции прямой с осью z.

3. Для построения профильного следа W_m прямой нужно фронтальную проекцию прямой продлить до пересечения с осью z в точке W″_m, которая является фронтальной проекцией профильного следа прямой m. Профильная проекция профильного следа, точка W″′_m, которая совпадает с самим профильным следом W_m, будет находиться на линии проекционной связи и на профильной проекции прямой m″′. Горизонтальная проекция профильного следа W′ находится в точке пересечения горизонтальной проекции прямой с осью y.

4. Для того, чтобы определить, через какие октанты проходит прямая, нужно на одной из проекций отметить одноименные проекции всех следов прямой. След прямой и есть точка перехода прямой из октанта в октант. После этого достаточно определить, в каком октанте находится хотя бы одна точка прямой в полученном интервале. В данном случае прямая проходит в IV – I – V – VI октантах.

Задание 2.9

Построить следы прямой, заданной отрезком AB, и определить, через какие октанты она проходит.

2.2.2. Натуральная величина отрезка прямой и углы наклона к плоскостям проекций

Пример 2.5

Определить натуральную величину отрезка AB и углы наклона его к плоскостям проекций H и V.

Решение (рис. 2.5)

Натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, один катет которого равен величине проекции, а другой - равен алгебраической разности расстояний концов другой проекции до разделяющей эти проекции оси. Угол наклона отрезка к плоскости, величина проекции на которую принята за катет, равен величине угла, прилежащего к этой проекции.

1. Для определения натуральной величины |AB| отрезка AB и угла α наклона к горизонтальной плоскости проекций, нужно построить прямоугольный треугольник, один катет которого равен величине горизонтальной проекции A′B′. Другой катет равен разности значений координат z для точек A и B. (z_A – z_B = Δz). Угол α определится, как угол, прилежащий к катету, равному горизонтальной проекции A′B′.

2. Для определения натуральной величины |AB| отрезка AB и угла β наклона к фронтальной плоскости проекций нужно построить прямоугольный треугольник, один катет которого равен величине фронтальной проекции A″B″. Другой катет равен разности значений координат y для точек A и B. (y_A – y_B = Δy). Угол β – определится, как угол, прилежащий к катету, равному фронтальной проекции A″B″.

Задание 2.10

Определить натуральную величину отрезка AB и углы наклона к плоскостям проекций H и V.

Задание 2.11

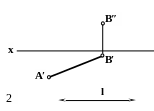
Достроить недостающую проекцию отрезка AB, действительная величина которого равна l.

Задание 2.12

Достроить недостающую проекцию отрезка AB, угол наклона которого к горизонтальной плоскости проекций равен а) 30^о, б) 45^о, в) 60^о.

Задание 2.13

Достроить недостающую проекцию отрезка AB, угол наклона которого к фронтальной плоскости проекций равен а) 30^о, б) 45^о, в) 60^о.

Задание 2.14

На луче m построить отрезок AB, действительная величина которого равна 40 мм.