3.2. Примеры решения задач

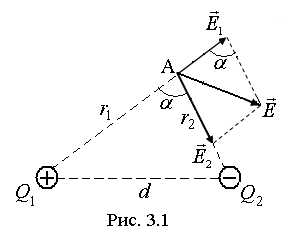
Пример 1. Два точечных электрических заряда Q_1=10 нКл и Q₂= -20 нКл находятся в среде с диэлектрической проницаемостью ε=2 на расстоянии d=10см друг от друга. Определить напряженность Е и потенциал j поля, создаваемого этими зарядами в точке А, удаленной от заряда Q₁ на расстояние r₁=10 см и от заряда Q₂ на расстояние r₂ =7 см.

Дано:

Q₁=10 нКл =10×10^-9 Кл

Q₂= -20 нКл = -20×10^-9 Кл

d = 10 см = 0,1 м

e = 2

r₁ = 10 см = 0,1 м

r₂ = 7 см = 0,07 м

e₀ = 8,85×10^-12 Ф/м  

Е = ? j = ?

Решение:

Согласно принципу суперпозиции электрических полей, каждый заряд создает электрическое поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена, как геометрическая сумма напряженностей и полей, создаваемых каждым зарядом в отдельности:

.

Модули напряженности электрических полей, создаваемых точечными зарядами Q₁ и Q₂ в среде с диэлектрической проницаемостью  рассчитываются по формулам:

, (3.1)

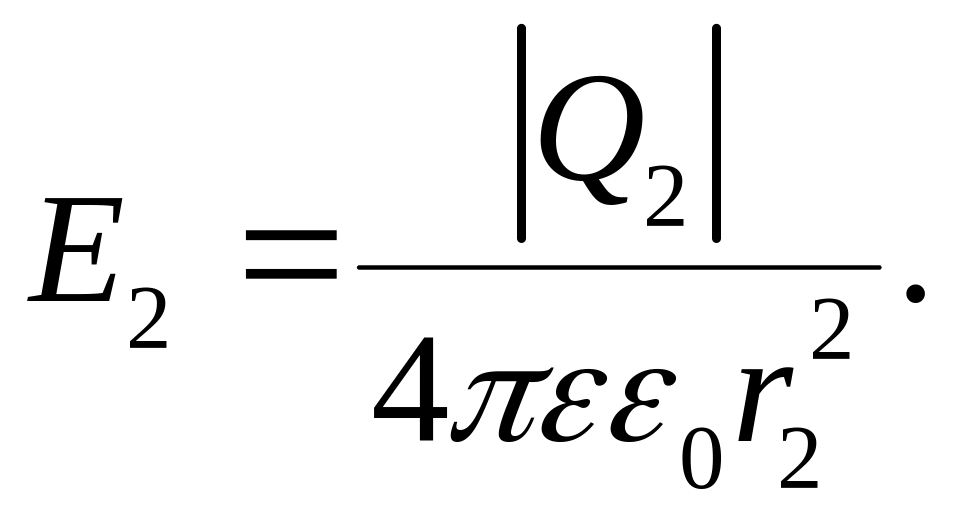(3.2)

Вектор (рис. 3.1) направлен по силовой линии от заряда Q₁, так как этот заряд положителен; вектор направлен также по силовой линии, но к заряду Q₂, так как этот заряд отрицателен.

Модуль вектора найдем по теореме косинусов

, (3.3)

где a -угол между векторами и в треугольнике А , который может быть найден из треугольника с известными сторонами r₁, r₂ и d:

.

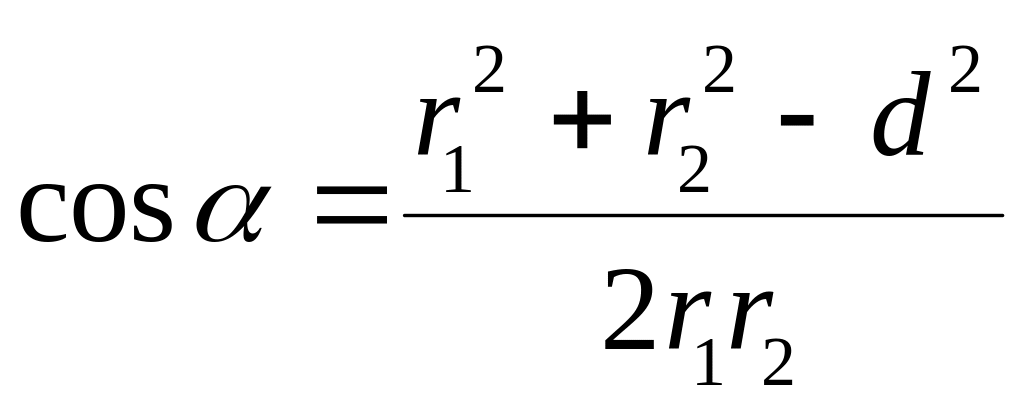В данном случае во избежание громоздких записей удобно значение cosa вычислить отдельно:

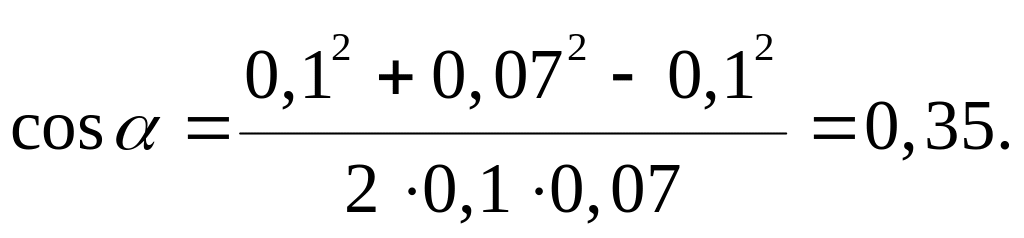
Подставляя выражение Е₁ из уравнения (3.1) и Е₂ из уравнения (3.2) в (3.3) и вынося общий множитель 1/(4pee₀) за знак корня, получаем

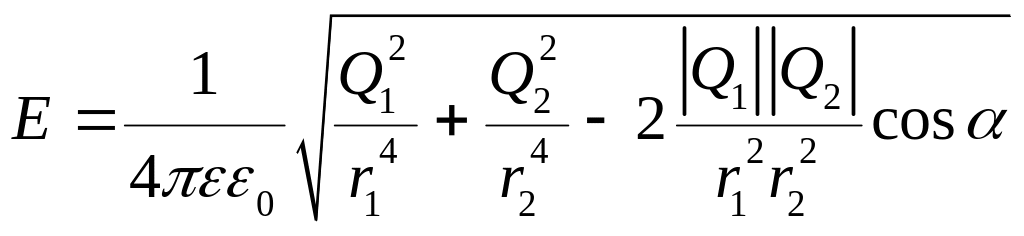. (3.4)

В соответствии с принципом суперпозиции электрических полей потенциал j результирующего поля, создаваемого двумя зарядами Q₁ и Q₂, равен алгебраической сумме потенциалов

. (3.5)

Потенциал электрического поля, создаваемого точечным зарядом Q на расстоянии r от него, выражается формулой

. (3.6)

В нашем случае согласно формулам (3.5) и (3.6) получим

или .

Произведем проверку единиц измерения:

.

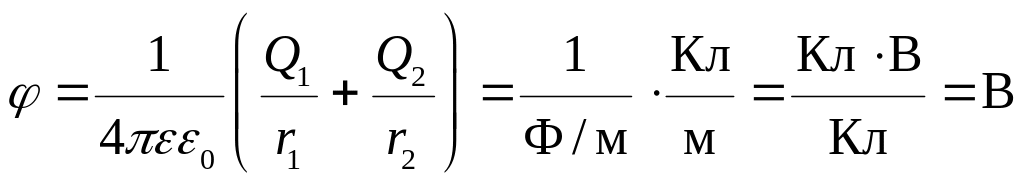Произведем вычисления:

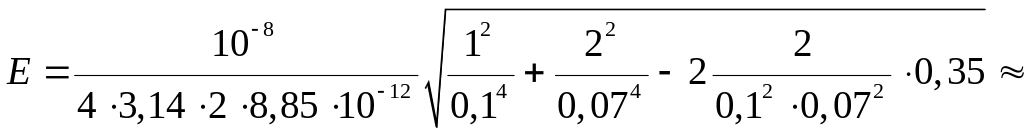
B/м;

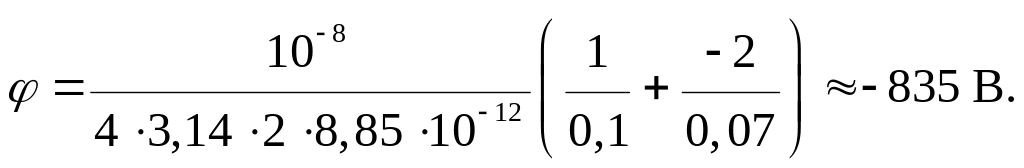
Ответ: Напряженность и потенциал в точке А соответственно равны Е = 5,6×10⁴ В/м, j = -835 В.

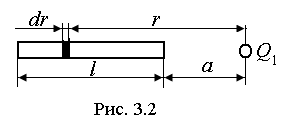
Пример 2. На тонком стержне длиной l=40см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а=20см от ближайшего конца находится точечный заряд Q_1=4нКл, который взаимодействует со стержнем с силой F=10мкН. Определить линейную плотность t заряда на стержне.

Дано:

l = 40 см = 0,4 м

а = 20 см = 0,2 м

Q₁= 4 нКл = 4×10^-9 Кл

F =10 мкН =10×10^-6 Н

e₀ = 8,85×10^-12 Ф/м 

t = ?

Решение:

Выделим из стержня (рис. 3.2) малый участок dr с зарядом dQ=tdr, где t - линейная плотность заряда. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона для точечных зарядов в вакууме, сила взаимодействия

.

Интегрируя это выражение в пределах от а до a+l получим,

.

Откуда

.

Произведем проверку единиц измерения:

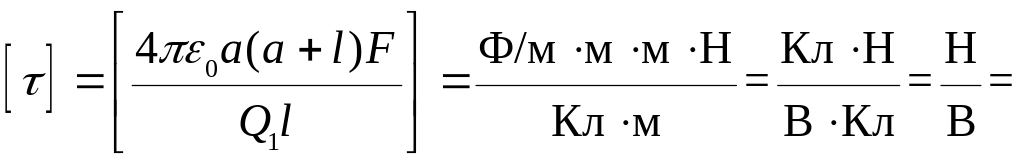
Произведем вычисления:

.

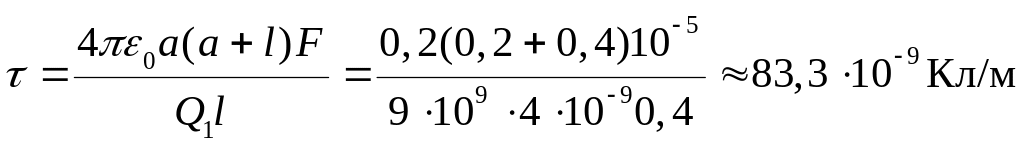Ответ: Линейная плотность заряда на стержне t=83,3×10^9Кл/м = 83,3 нКл/м.

П

Дано:

ε = 9

q = 1×10^-9 Кл

r = 1 см = 0,01 м

R = 9 см = 0,09 м

s = 1×10^-4 Кл/м²

e₀ = 8,85×10^-12 Ф/м 

А=?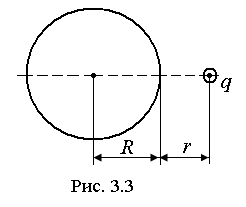

ример 3. Заряд q=2×10^-9 Кл переносится из бесконечности в точку, находящуюся на расстоянии r=1см от поверхности заряженного шара радиусом R=9см. Поверхностная плотность положительного заряда s=10^‑4 Кл/м². Определить совершаемую при этом работу, если диэлектрическая проницаемость среды ε=9.

Решение:

Работа A внешней силы по перемещению заряда q из точки поля с потенциалом j₁ в другую точку с потенциалом j₂ равна по абсолютной величине, но противоположна по знаку работе сил поля по перемещению заряда между этими точками поля, то есть

Работа сил электрического поля определяется по формуле

.

Тогда

, (3.7)

где j₁ – потенциал в начальной точке; j₂ – потенциал в конечной точке.

Потенциал, создаваемый заряженным шаром радиусом R в точке на расстоянии r от его поверхности, определяется по формуле

, (3.8)

где Q = 4spR² – заряд шара.

Потенциал j₁ в бесконечно удаленной точке (при r¥) будет равна нулю. Воспользуемся выражением (3.8) для потенциала j₂ и подставим в формулу (3.7); после преобразований получим

.

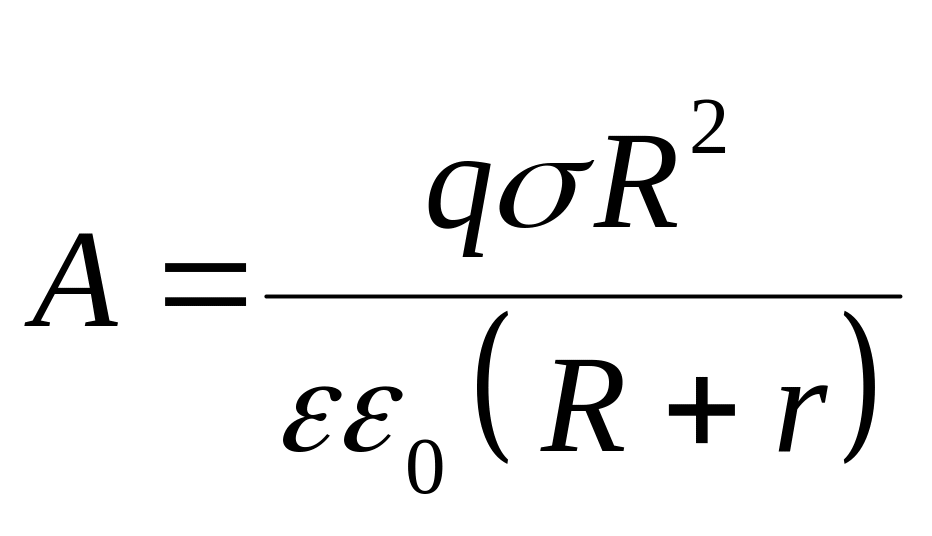Проверим единицы измерения:

.

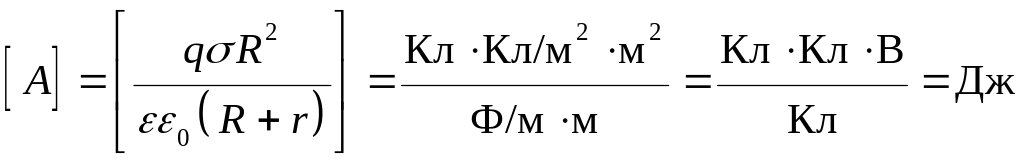Расчет:

.

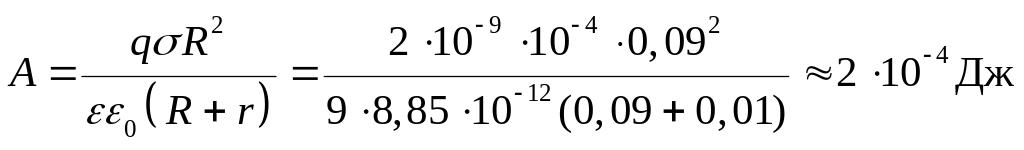Ответ: Работа перемещения заряда из бесконечности в данную точку поля равна А = 2×10^-4 Дж.

Пример 4. Между пластинами плоского конденсатора, находящимися на расстоянии d_0=1см, приложена разность потенциалов U_1=200В. К одной из пластин конденсатора прилегает плоскопараллельная стеклянная пластина (e_1=7) толщиной d_1=9мм. Конденсатор отключают от источника напряжения и после этого вынимают пластину. Определить разность потенциалов между пластинами конденсатора. Во сколько раз изменится энергия конденсатора?

Дано:

d₀ = 1см = 0,01 м

d₁ = 9 мм = 9×10^-3 м

U₁ = 200 В

e₁ = 7

e₂ = 1 

U₂ =? W₂/W₁=?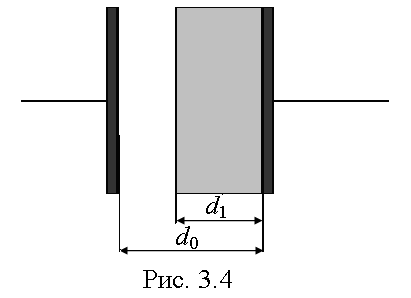

Решение:

Разность потенциалов между пластинами конденсатора в случае отключения его от источника напряжения находится из условия, что заряд на его пластинах остается неизменным, то есть

, (3.9)

где С₁ и С₂ – емкости конденсатора; U₁ и U₂ – разности потенциалов.

В условиях данной задачи конденсатор вначале является слоистым и его емкость С₁ находится по формуле, используемой для определения емкости батареи последовательно соединенных конденсаторов

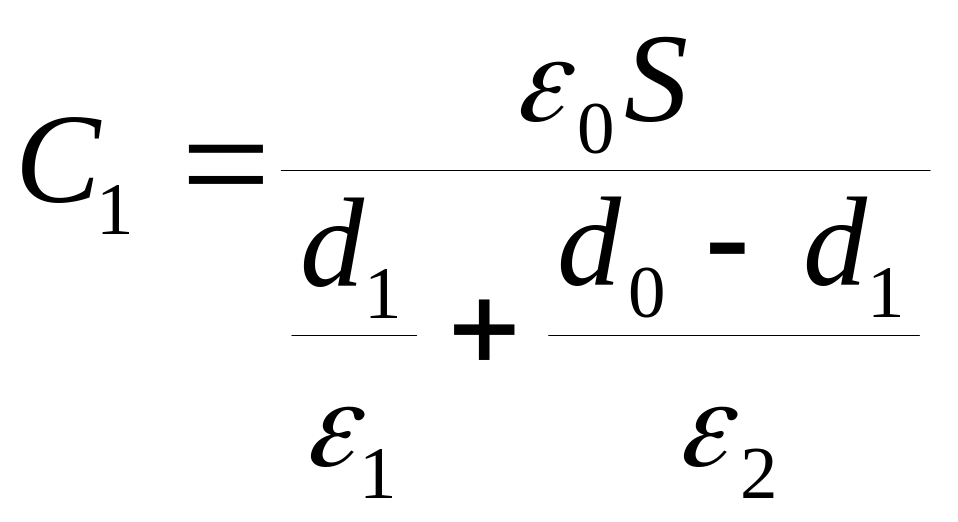, (3.10)

где S – площадь пластин; e₁ и e₂ – диэлектрические проницаемости стекла и воздуха; d₁ – толщина стеклянной пластины; d₀ – зазор между пластинами.

После удаления стеклянной пластины из зазора конденсатор становится простейшим плоским конденсатором с емкостью

. (3.11)

Разность потенциалов U₂, которая устанавливается после удаления из зазора стеклянной пластины, определим из формулы (3.9), подставляя в нее формулы (3.10) и (3.11) и производя соответствующие преобразования:

. (3.12)

Энергия заряженного конденсатора:

.

Изменение энергии конденсатора найдем, узнав отношение энергии конденсаторов:

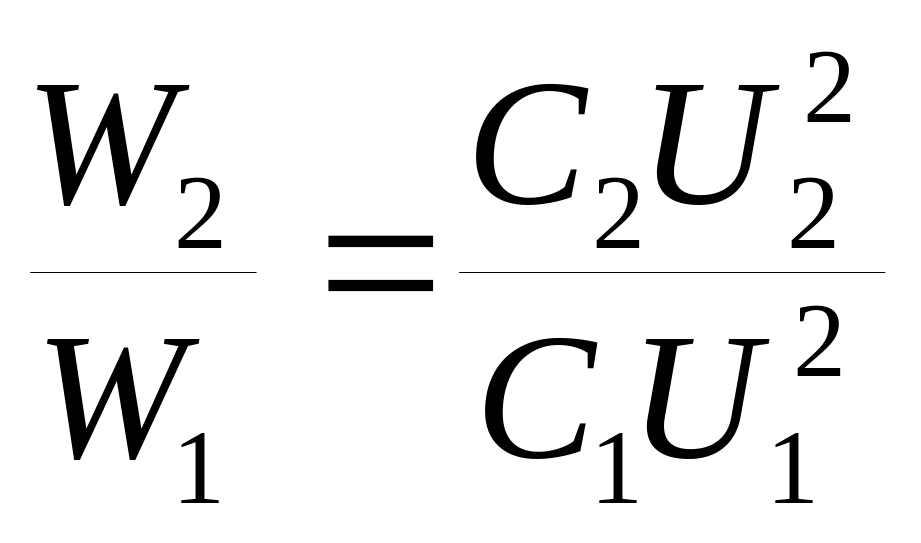. (3.13)

Это отношение можно определить двумя способами:

1. Если подставить выражение для входящих в отношение (3.13) величин, то после преобразований и вычислений получим:

.

2. Отношение (3.13) можно представить в виде

.

Так как по условию С₁U₁= C₂U₂ (см.(3.9)), то

.

Делаем проверку единиц измерения:

.

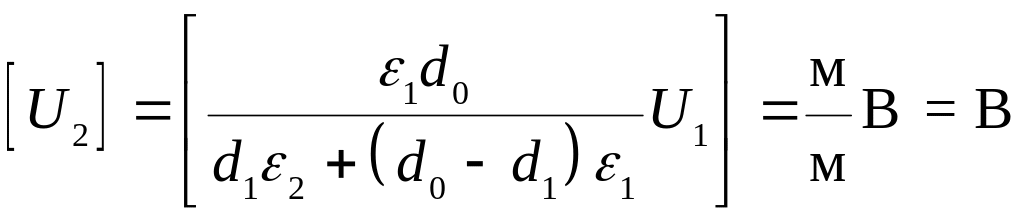Расчет:

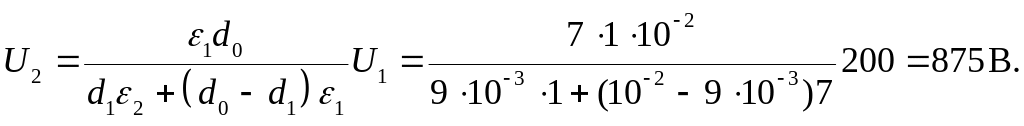
Ответ: После выемки стеклянной пластины разность потенциалов между пластинами конденсатора станет равной 875В, а энергия увеличится в 4,38 раза.

П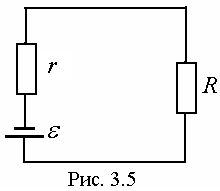 ример 5. Определить максимальную мощность, которая может выделяться во внешней цепи, питаемой от батареи с ЭДС 12В, если наибольшая сила тока, которую может дать батарея, равна = 5 А.

Дано:

e = 12 В

I_maх = 5 А 

Р_max = ?

Решение:

Используем Закон Ома для полной цепи:

, (3.14)

где R – сопротивление внешней цепи; r – внутреннее сопротивление источника тока.

Мощность Р, выделяемая во внешней цепи, определяется по формуле . Преобразуем это выражение, используя формулу (3.14):

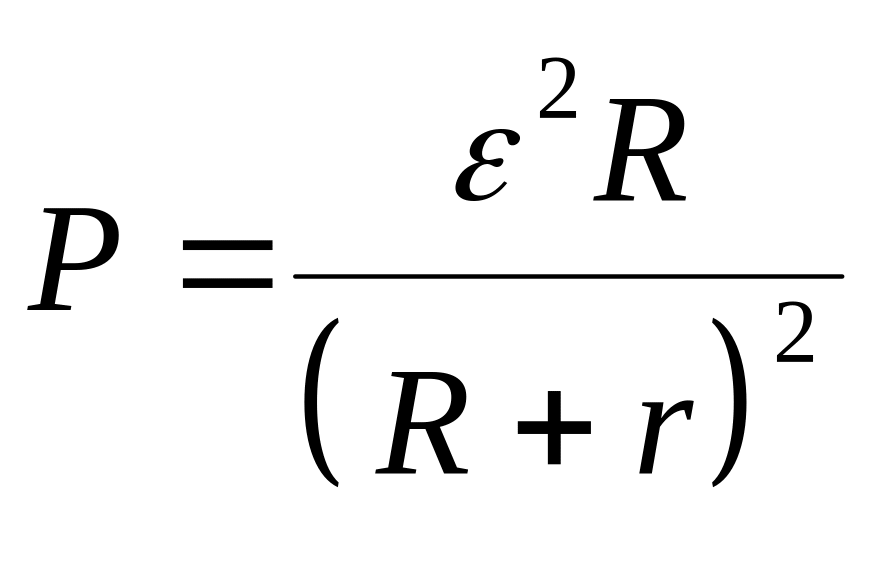. (3.15)

Таким образом, мощность зависит от внешнего сопротивления цепи R. Мощность будет максимальной при таком значении R, при котором производная dР/dR обращается в нуль.

Возьмем первую производную и приравняем к нулю:

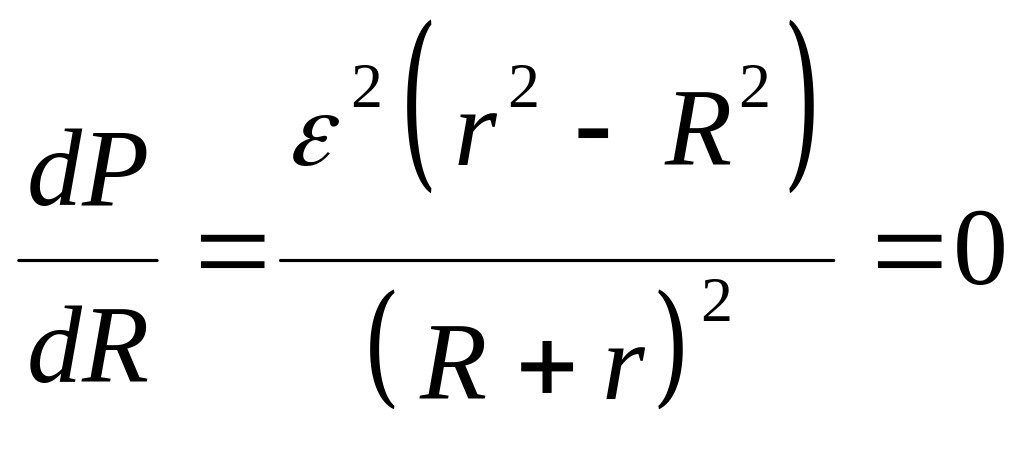. (3.16)

Тогда получим R = r. Определим r.

Максимальный ток возникает при коротком замыкании цепи, т.е. когда внешнее сопротивление R=0. Исходя из этого, , откуда , значит

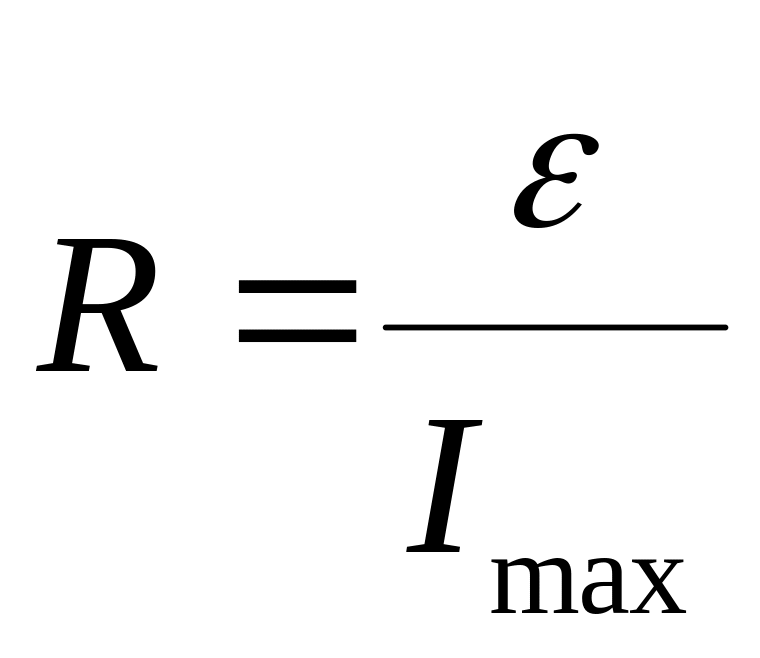. (3.17)

Подставив уравнение (3.17) в уравнение (3.15) и выполнив преобразования, получим:

. (3.18)

Проверка единиц измерения:

.

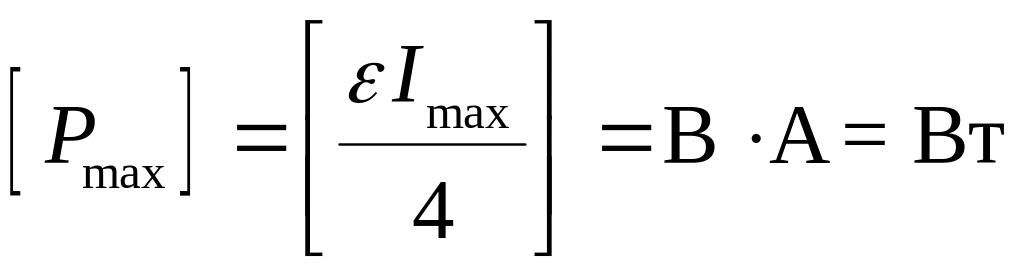Расчет:

.

Ответ: Максимальная мощность, выделяемая во внешней цепи, равна 15 Вт.

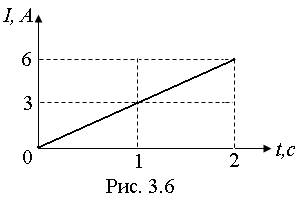
Пример 6. Сила тока в проводнике сопротивлением R=20Ом нарастает в течении времени Dt=2с по линейному закону от I_0=0 до I=6А (рис. 3.6). Определить теплоту Q, выделившуюся в этом проводнике за вторую секунду.

Дано:

R = 20 Ом

Dt = 2 с

I₀ = 0

I = 6 A 

Q = ?

Решение:

Закон Джоуля – Ленца в виде справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде

. (3.19)

Здесь сила тока I является некоторой функцией времени. В данном случае

, (3.20)

где – сила тока в начальный момент времени, k – коэффициент пропорциональности, характеризующий скорость изменения силы тока. Как видно из рис. 3.6

.

С учетом формулы (3.20) формула (3.19) примет вид

. (3.21)

Для определения теплоты, выделившейся за конечный интервал времени Dt, выражение (3.21) надо проинтегрировать в пределах от t₁ до t₂:

.

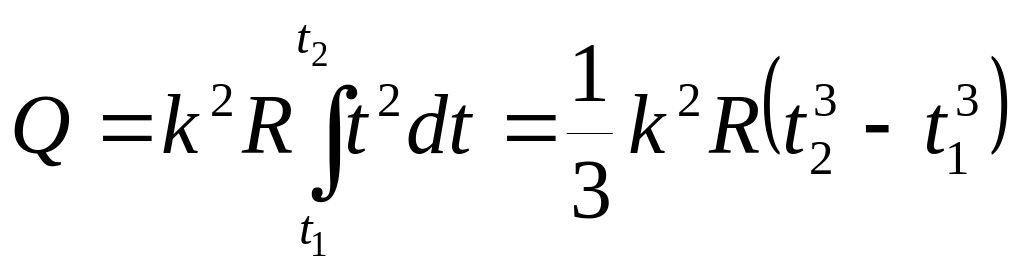Проверка единиц измерения:

.

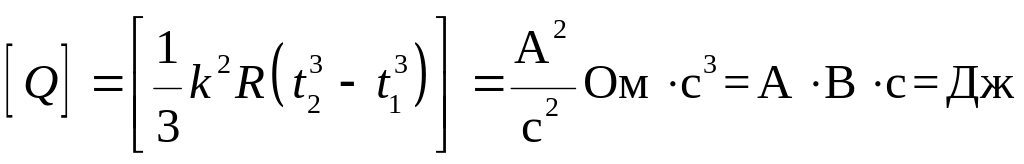Расчет:

Дж.

Ответ: За вторую секунду в проводнике выделится 420 Дж теплоты.