4. Структура общего решения неоднородной системы уравнений. Алгоритм метода Гаусса построения общего решения линейной алгебраической системы уравнений
Рассмотрим
неоднородную систему (1). Сначала заметим,
что разность
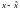двух ее решений будет решением
соответствующей однородной системы
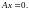Действительно, имеем верные равенства
и
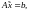поэтому
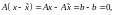т.е. разность
является решением однородной системы
(2). Отсюда следует, что вектор
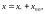где
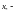фиксированное решение неоднородной
системы
,
а
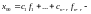общее решение соответствующей однородной
системы
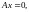будет решением неоднородной системы
(1) при любых значениях постоянных
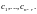Если
теперь
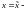любое другое решение неоднородной
системы
,
то его можно представить в виде
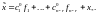Действительно, разность
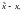является решением однородной системы
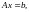а,
значит, по теореме 1 существуют постоянные
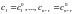такие, что имеет место равенство
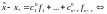
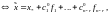ч.т.д.
Мы получили следующий результат.
Теорема 2. Общее решение неоднородной системы имеет вид
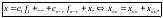
где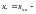
частное решение неоднородной системы
,
фундаментальная
система решений соответствующей
однородной системы
а
произвольные постоянные.
Теперь опишем алгоритм построения общего решения неоднородной системы (1).
Алгоритм метода Гаусса
1.
По системе (1) строим расширенную матрицу
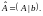
2.
С помощью элементарных преобразований
строк приводим матрицу
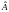к ступенчатому виду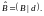
3.
По матрице
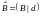восстанавливаем систему уравнений;
при этом уравнения, соответствующие
нулевым строкам матрицы
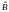не выписываем.
4. Неизвестные,
коэффициентами которых являются опорные
элементы матрицы
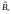объявляем
базисными (закрепленными), оставляем
их в левых частях уравнений, а остальные
неизвестные объявляем свободными и
переносим их в правые части уравнений.
5. Придавая свободным неизвестным значения произвольных постоянных, решаем полученную систему уравнений обратным ходом и находим базисные неизвестные и , наконец, записываем общее решение исходной системы уравнений в виде (4).
Пример 1. Найти общее решение системы уравнений
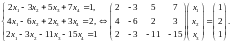
Решение. Составляем расширенную матрицу и приводим её к ступенчатому виду (опорные элементы выделены в квадратиках):
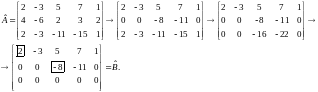
По матрице восстанавливаем систему уравнений (нулевую строку не учитываем):
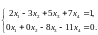
Базисными
неизвестными являются
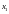и
;
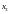оставляем их слева. Полагая значения
свободных неизвестных произвольными:
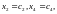перенесём
их направо. Будем иметь
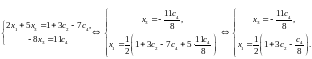
Теперь можно записать общее решение исходной системы (5):
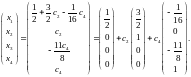
Отсюда и из теоремы 2 следует, что
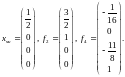
Найдены
частное решение
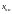системы (5) и ф.с.р. соответствующей
однородной системы.
Лекция 5. Правило Крамера. Линейное подпространство. Линейный оператор и его матрица в фиксированном базисе. Алгебра линейных операторов и ее связь с алгеброй матриц
В предыдущей лекции были рассмотрены общие системы линейных уравнений. В них число уравнений могло не совпадать с числом неизвестных. Соответствующая матрица системы была в общем случае прямоугольной. В случае систем с квадратной матрицей можно указать еще два способа решения (кроме изложенного выше метода Гаусса).