2. Линейные системы алгебраических уравнений. Теорема Кронекера-Капелли

Системой уравнений с неизвестными называется система вида

где 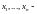неизвестные, 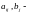известные числа (коэффициенты системы), 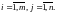Вводя обозначения

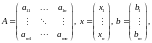
можно записать систему (1) в краткой форме 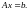Её называют матричной формой записи системы (1). При этом столбец называют столбцом неизвестных, матрицу 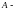матрицей системы (1), а столбец 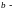столбцом свободных членов (или правых частей) системы (1). Если столбец свободных членов 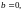то система (1) называется однородной системой; если 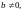то (1) называется неоднородной системой.

Определение 1. Решением системы (1) называется совокупность неизвестных 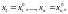которая, будучи подставленная в уравнения (1), обращает их в верные числовые равенства (другое определение: решением системы (1) называется вектор-столбец 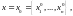обращающий систему 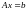в истинное векторное равенство 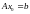). При этом если система (1) имеет хотя бы одно решение, то она называется совместной (или разрешимой). Если (1) не имеет решений, то она называется несовместной (или неразрешимой). Система, имеющая только одно решение, называется определённой системой. Система, имеющая более одного решений, называется неопределённой системой.

Рассмотрим систему (1) в матричной форме Как уже говорилось выше, называется матрицей коэффициентов или просто матрицей системы (1) . Если к этой матрице присовокупить справа столбец 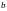свободных членов, то получим матрицу 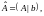называемую расширенной матрицей системы уравнений (1). Эта матрица играет важную роль в теории линейных систем уравнений. Например, по ней можно судить, будет ли система (1) разрешимой или нет. Имеет место следующее утверждение.

Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместной необходимо и достаточно, чтобы

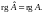
Следствие 1. Однородная система 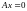всегда совместна (это утверждение вытекает также из того, что однородная система имеет тривиальное решение ).

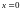3. Линейные пространства и базис. Структура общего решения однородной системы уравнений

Рассмотрим теперь более подробно однородную систему

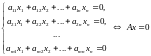
и попробуем установить свойства ее решений. Сначала введем некоторые понятия, о которых подробно будет сказано в следующих лекциях.

Определение 2. Произвольное множество 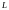называется линейным пространством над множеством чисел , если в нем для любых двух элементов 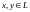введены две операции: операция сложения (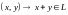 ) и операция умножения на числа (

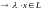), подчиняющиеся следующим аксиомам:

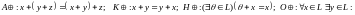
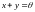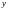( элемент называется обратным или противоположным к элементу и обозначается 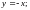элемент 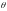называется нулевым или нейтральным элементом пространства );

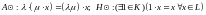(элемент 1 называется нейтральным элементом умножения на числа);

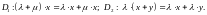
Здесь везде произвольные элементы множеств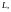а а 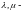произвольные числа из 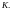Нейтральный элемент обычно отождествляют с нулем:

Элементы линейного пространства часто называют векторами и мы будем в дальнейшем также пользоваться этим термином. Простейшими примерами линейных пространств являются множества 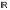действительных чисел (с естественными операциями сложения и умножением на числа), а также пространство геометрических векторов, рассмотренное ранее, с введенными в нем линейными операциями сложения и умножения на действительные числа. В качестве другого важного примера линейного пространства можно указать на пространство 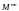матриц размера с введенными ранее операциями сложения матриц и умножения их на числа. В частности, линейными пространствами будут пространство столбцов:

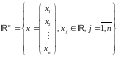
и пространство строк: .

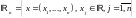Ранее было введено понятие линейной зависимости и линейной независимости строк и столбцов. Точно такие же понятия вводятся и в произвольном линейном пространстве

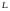
Определение 3. Упорядочная система векторов 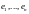линейного пространства называется базисом в , если она удовлетворяет следующим требованиям:

1) система линейно независима; 2) каков бы ни был вектор 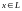существуют числа 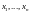такие, что имеет место представление

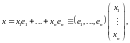
причем это представление единственно. Числа называются координатами вектора в базисе 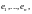а столбец 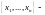координатным столбцом вектора

Заметим, что если в пространстве существует базис, состоящий из конечного числа векторов, то пространство называется конечномерным ( мерным; пишут размерность пространства ). В противном случае называется бесконечномерным пространством. Так же, как и в трехмерном пространстве геометрических векторов, устанавливается взаимно однозначное соответствие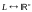 между элементами 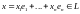и их координатными столбцами 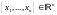по закону:

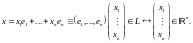
Нетрудно видеть, что это соответствие² сохраняет линейные операции, поэтому вместо линейных действий над векторами пространства производят аналогичные действия над их координатами. Перейдем теперь к рассмотрению линейной однородной системы (2). Используя теорему о базисном миноре и тот факт, что линейная система (2) равносильна системе с матрицей ступенчатого вида, полученной из матрицы эквивалентными преобразованиями строк, докажем следующий результат.

Теорема 1. Множество всех решений однородной системы (2) (состоящей из уравнений с неизвестными) образует линейное пространство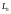 размерности

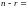
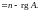При этом любое решение однородной системы (2) имеет вид

где 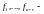базис пространства решений (его называют фундаментальной систе-

мой решений однородной системы (2)), а 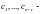некоторые постоянные.

Заметим, что линейная комбинаци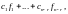я где произвольные постоянные, фундаментальная система решений системы (2),называется общим решением этой системы и обозначается

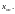
Таким образом, построение общего решения системы (2) сводится к построению её фундаментальной системы решений (ф.с.р.). Как найти ф.с.р.? Ответу на этот вопрос мы предпошлем описание алгоритма построения общего решения неоднородной системы (1).