
- •1. Векторы. Координаты векторов и линейные операции над векторами
- •2. Скалярное, векторное и смешанное произведение векторов
- •1. Общее уравнение плоскости и уравнение в отрезках
- •2. Особые случаи расположения плоскости в пространстве
- •3. Условия параллельности и перпендикулярности плоскостей. Угол между двумя плоскостями
- •4. Решение различных задач на плоскость
- •5. Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •6. Прямая в пространстве
- •1. Матрицы и действия над ними. Матрицы специального вида
- •2. Определители матрицы и их свойства
- •3. Обратимость матриц. Вычисление обратной матрицы
- •4. Ранг матриц. Теорема о базисном миноре
- •1. Элементарные преобразования и приведение матриц к ступенчатому виду
- •2. Линейные системы алгебраических уравнений. Теорема Кронекера-Капелли
- •3. Линейные пространства и базис. Структура общего решения однородной системы уравнений
- •4. Структура общего решения неоднородной системы уравнений. Алгоритм метода Гаусса построения общего решения линейной алгебраической системы уравнений
- •1. Линейные системы уравнений с квадратной матрицей. Правило Крамера
- •2. Линейный оператор и его матрица в фиксированном базисе. Алгебра линейных операторов и ее связь с алгеброй матриц
- •1.Изменение координат вектора и матрицы оператора при переходе к новому базису
- •2. Ядро и образ линейного оператора
- •3. Собственные значения и собственные векторы линейного оператора. Матрица оператора в базисе из собственных векторов
6. Прямая в пространстве
Прямой в пространстве называют линию пересечения двух непараллельных плоскостей. Значит, прямая в пространстве задается системой уравнений
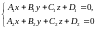
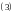
при
условии отсутствия пропорциональности
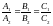 между коэффициентами линейных уравнений,
входящих в систему (3). Однако наиболее
распространенным уравнением прямой
являются каноническое
уравнение.
Выведем его
между коэффициентами линейных уравнений,
входящих в систему (3). Однако наиболее
распространенным уравнением прямой
являются каноническое
уравнение.
Выведем его
Определение
2. Вектор
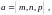 параллельный прямой
параллельный прямой
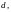 называется
направляющим
вектором
этой прямой.
называется
направляющим
вектором
этой прямой.
Теорема
3. Если
фиксированная точка прямой
а
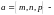 направляющий
вектор этой прямой, то любая точка
направляющий
вектор этой прямой, то любая точка
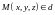 связана уравнением
связана уравнением
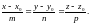
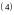
Уравнение
(4) называют каноническим
уравнением прямой
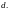
Доказательство.
Вектор
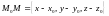 коллинеарен
вектору
=
коллинеарен
вектору
=
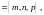 а,
значит, их координаты пропорциональны,
т.е. имеют место равенства (4). Если же
точка
а,
значит, их координаты пропорциональны,
т.е. имеют место равенства (4). Если же
точка
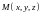 не лежит на прямой
то векторы
не лежит на прямой
то векторы
и
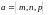 не
коллинеарны, поэтому равенства (4) не
имеют места. Теорема доказана.
не
коллинеарны, поэтому равенства (4) не
имеют места. Теорема доказана.
Если
приравнять равные отношения (4) коэффициенту
пропорциональности
 то получим уравнения
то получим уравнения
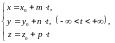
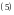
задающие
прямую
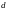 параметрически (здесь
параметрически (здесь
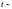 параметр).
Изменяя
мы получим все точки
параметр).
Изменяя
мы получим все точки
прямой
(например, при
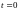 получает точку
получает точку
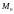 ).
).
Как
получить из системы уравнений (3)
канонические уравнения прямой
?
Пусть
произвольная
точка, удовлетворяющая системе (3) (ее
можно получить, например, фиксируя
произвольным образом координату
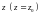 ,
а затем решить полученную систему
уравнений с двумя неизвестными). Далее,
векторы
,
а затем решить полученную систему
уравнений с двумя неизвестными). Далее,
векторы
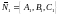 и
и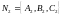 перпендикулярно
соответствующим плоскостям в (3), а,
значит, векторное призведение
перпендикулярно
соответствующим плоскостям в (3), а,
значит, векторное призведение
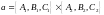 параллельно
их общей прямой – линии их пересечения.
Отсюда следует, что
параллельно
их общей прямой – линии их пересечения.
Отсюда следует, что
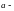 направляющий вектор прямой
.
Поскольку
направляющий вектор прямой
.
Поскольку
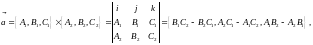
то кононическим уравнением прямой будет уравнение
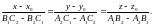
Ясно,
что углом
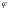 между двумя прямыми
между двумя прямыми
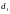 и
и
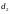 (точнее, одним из них; обычно берут
острый
угол)
является угол между их направляющими
векторами,
поэтому
(точнее, одним из них; обычно берут
острый
угол)
является угол между их направляющими
векторами,
поэтому
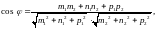
где
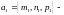 направляющий вектор прямой
направляющий вектор прямой
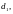 а
а
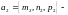 направляющий
вектор прямой
направляющий
вектор прямой
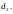 При этом если
При этом если
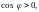 то угол между прямыми будет острый. Из
последней формулы получаем следующие
утверждения.
то угол между прямыми будет острый. Из
последней формулы получаем следующие
утверждения.
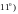
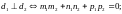
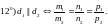
Используя
полученные сведения о прямой и плоскости,
можно без труда решать различные задачи
аналитической геометрии. Решим, например,
задачу о нахождении точки пересечения
прямой (5) и плоскости (2). Подставляя
равенства (5) в уравнение (2), получим
уравнение
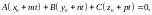 решая которое, найдем параметр
решая которое, найдем параметр
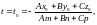 при котором происходит пересечение
прямой и плоскости. Подставляя его в
(5), найдем точку пересечения
при котором происходит пересечение
прямой и плоскости. Подставляя его в
(5), найдем точку пересечения
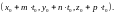
Лекция 3. Матрицы. Операции над матрицами. Матрицы специального вида. Квадратные матрицы и их определители. Свойства определителей. Обратные матрица и условие ее существования. Ранг матрицы
В теории систем линейных уравнений, в дифференциальных уравнениях и др. математичеких объектах большую роль играют матрицы – таблицы чисел, с помощью которых можно не только компактно записать системы уравнений, но и, производя над ними определенные действия, решать сами уравнения. Перейдем к изложению основных понятий и утверждений, связанным с матрицами.
