6.2. Обслуживание вызовов системой с ожиданием

Пусть задана коммутационная система, в выходы которой включен полнодоступный пучок емкостью v (v < 1), обслуживающий простейший поток вызовов. Если в момент поступления вызова все v линий заняты, то для системы с ожиданием вызов теряется лишь на время, но само сообщение не теряется, а становится в очередь на ожидание до освобождения занятых другими вызовами линий пучка. Поступающие на ожидание вызовы могут образовать очередь различной длины r, при этом число мест для ожидания неограничено. Дисциплина с ожиданием заключается в том, что при наличии свободных линий поступающий вызов немедленно обслуживается. Если все v линий заняты, то вызов ставится в очередь на ожидание до освобождения другими вызовами хотя бы одной линии пучка. Вызовы, находящиеся на ожидании, обслуживаются в порядке очереди.

Длительность занятия линий обслуживанием вызова t_з является случайной величиной, распределенной по показательному закону

F(t) = P(tз < t) = 1-e^-βt, (6.29)

где β - параметр показательного закона распределения, обратный средней длительности занятия .

Требуется определить вероятности различных состояний полнодоступного пучка линий и длины очереди вызовов, находящихся на ожидании, функцию распределения длительности ожидания вызовом начала обслуживания, среднее время ожидания и среднюю длину очереди.

Состояние системы в произвольный момент времени t обозначим через i (число вызовов, находящихся в системе). Если в момент t в системе находятся i < v вызовов, то все они находятся на обслуживании. При i = v + r на обслуживании находятся v вызовов (заняты все v линий пучка), а остальные r = i - v вызовов находятся на ожидании.

Вероятности состояний полнодоступного пучка можно записать в следующем виде:

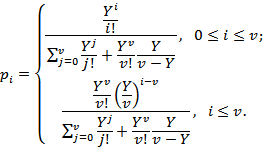(6.30)

Формула (6.29) описывает распределение Эрланга для системы с ожиданием. При ограничении числа состояний системы 0 ≤ i ≤ v, т.е. при переходе к системе с потерями, вероятности состояний p_i рассчитываются по первой формуле Эрланга, т.е.

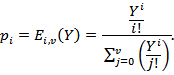(6.31)

Сопоставим значения вероятности состояний p_i в системе с ожиданием и вероятности числитель и знаменатель соотношения (6.31) на E_i,_y(Y). Тогда это соотношение преобразуется к виду состояний в системе с потерями. С этой целью разделим числитель и знаменатель соотношения (6.30) на Тогда это соотношение

преобразуется к виду

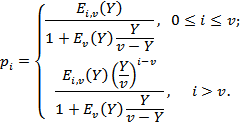(6.32)

Поскольку в (6.32) знаменатель больше 1, то р_i < E_i,v(Y) для всех значений i (0 ≤ i ≤ v). Следовательно, для систем с ожиданием время нахождения в состояниях, когда поступающие вызовы немедленно обслуживаются, меньше, чем для систем с потерями.

В системах с ожиданием потери по времени р_t есть доля времени, в течение которой все v линий пучка заняты и на ожидании находится r = 1, 2, ... вызовов. Исходя из этого потери по времени равны вероятности р(γ > 0) того, что поступивший вызов не будет немедленно обслужен, а будет ожидать начала обслуживания в течение времени γ > 0. Эта вероятность равна

(6.33)

Однако при расчетах используют выражение

(6.34)

Выражение (6.34) называется второй формулой Эрланга. Формула табулирована. Таблицы позволяют по двум из трех параметров - Y, v, p_t – определить третий. Из (6.34) видно, что D_v(Y) > E_v(Y), т.е. при одинаковых значениях интенсивности нагрузки и числе линий вероятность ожидания в системе с ожиданием выше, чем вероятность потери вызова в системе с явными потерями. Это объясняется тем, что в системе с явными потерями поступивший в момент занятости всех линий вызов теряется и никакого воздействия на систему в последующем не оказывает, а в системе с ожиданием вызовов ставится на ожидание.

При освобождении линии в системе с явными потерями она предоставляется поступающему вызову, а в системе с ожиданием при наличии очереди - ожидающему. Вновь поступившему вызову приходится становиться в очередь. Так как вызов не теряется, а лишь задерживается при обслуживании, то вероятность ожидания (6.34) называют условными потерями.

Условные потери во времени р_t = р(γ > 0) могут быть также определены и с помощью таблиц первой формулы Эрланга. Используя эти таблицы, р_t можно определить из следующего соотношения:

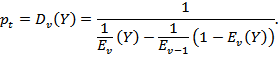(6.35)

Как в системах с ожиданием, так и в системах с потерями при обслуживании полнодоступным пучком вызовов простейшего потока вероятность потерь по времени и вероятности состояний системы зависят только от интенсивности поступающей нагрузки Y и емкости пучка линий v.

Полученная характеристика р_t=р(γ>0)=D_v(Y) определяет долю вызовов, обслуживание которых происходит после некоторого времени ожидания, однако не дает ответа на важный, с точки зрения обеспечения качества обслуживания, вопрос - как распределяется время ожидания начала обслуживания для вызовов, которые попадают на ожидание. В связи с этим определим функцию распределения длительности ожидания начала обслуживания при условии, что вызовы обслуживаются в порядке очереди.

Обозначим через р(γ > t) вероятность того, что вызов, поступивший в произвольный момент времени, попадет на ожидание и время ожидания будет больше t; через p_i (γ>t) - условную вероятность того же неравенства, но в предположении, что вызов поступит в момент времени, когда система находится в состоянии i. Вероятность р_i - это вероятность того, что в системе имеется i обслуживаемых и ожидающих вызовов.

Учитывая, что в коммутационной системе поступивший вызов попадает на ожидание лишь в случае, когда заняты все линии пучка и на ожидании находится r = 0, 1, 2, ... вызовов (т.е. система находится в состоянии i = v, v+l, v+2, ...,), то по формуле полной вероятности

. (6.36)

Если система находится в состоянии i (i > v), то непосредственно перед моментом поступления вызова в системе на ожидании находится (i - v) вызовов. Поступивший вызов становится в очередь и является в очереди (i - v+l) - M.

Поскольку вызовы снимаются с очереди для обслуживания в порядке поступления (первым пришел - первым обслуживается), то вероятность p_i(γ>t)

есть вероятность того, что за время t после момента поступления вызова будет снято с ожидания и переведено на обслуживание не более (i - 1) вызовов. Исходя из этого вероятность p_i(γ>t) соответствует вероятности того, что за время t произойдет освобождение не более (i - v) вызовов.

Если за единицу измерения времени γ и t принять среднюю длительность занятия, то вероятность p_i(γ>t) можно рассчитать по формуле

. (6.37)

К характеристикам процесса обслуживания поступающего потока вызовов в системах с ожиданием, кроме р(γ > 0) и р(γ > t), относятся:

• среднее время ожидания начала обслуживания γ, отнесенное ко всем поступающим вызовам;

• среднее время ожидания начала обслуживания γ_з, отнесенное к вызовам, попадающим на ожидание (задержанным с обслуживанием);

• средняя длина очереди r .

Эти величины можно найти из следующих выражений:

(6.38)

; (6.39)

или в единицах средней длительности занятия

(6.40)

Из (6.40) следует, что средняя длина очереди определяется как среднее время ожидания начала обслуживания вызова, отнесенное ко всем поступающим вызовам, умноженное на интенсивность поступающей нагрузки.