ТЕМА 6

Функции случайных величин

Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей и плотности для функции двух случайных аргументов.

1. Закон распределения функции одной случайной величины.

При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др. часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции тоже являются случайными величинами. Поэтому при решении таких задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно закон распределения системы случайных аргументов известен и известна функциональная зависимость.

Таким образом, возникает задача, которую можно сформулировать следующим образом.

Дана система случайных величин , закон распределения которой известен. Рассматривается некоторая случайная величина как функция данных случайных величин:

. (6.1)

Требуется определить закон распределения случайной величины , зная вид функции (6.1) и закон совместного распределения ее аргументов.

Рассмотрим задачу о законе распределения функции одного случайного аргумента

.

Вначале пусть - дискретная случайная величина, имеющая ряд распределения:

			...
			...

Тогда - также дискретная случайная величина с возможными значениями , , ... , . Если все значения , , ... , различны, то для каждого события и тождественны. Следовательно,

и искомый ряд распределения имеет вид:

			...
			...

Если же среди чисел , , ... , есть одинаковые, то каждой группе одинаковых значений нужно отвести в таблице один столбец и соответствующие вероятности сложить.

Для непрерывных случайных величин задача ставится так: зная плотность распределения случайной величины , найти плотность распределения случайной величины . При решении поставленной задачи рассмотрим два случая.

Предположим сначала, что функция является монотонно возрастающей, непрерывной и дифференцируемой на интервале , на котором лежат все возможные значения величины . Тогда обратная функция существует, при этом является также монотонно возрастающей, непрерывной и дифференцируемой функцией. В этом случае получаем:

. (6.2)

Пример 1. Случайная величина ораспределена с плотностью

.

Найти закон распределения случайной величины , связанной с величиной зависимостью

.

Решение. Так как функция монотонна на промежутке , то можно применить формулу (6.2). Обратная функция по отношению к функции есть , ее производная . Следовательно,

.

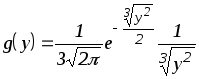Рассмотрим случай немонотонной функции. Пусть функция такова, что обратная функция неоднозначная, т. е. одному значению величины соответствует несколько значений аргумента , которые мы обозначим через , , ... , , где - число участков, на которых функция изменяется монотонно. Тогда

. (6.3)

Пример 2. В условиях примера 1 найти распределение случайной величины

.

Решение. Обратная функция неоднозначна. Одному значению аргумента соответствует два значения функции :

.

Применяя формулу (6.3), получим:

.