Построение таблиц истинности для сложных функций
Выписать значения которые могут принимать наборы переменных этой функции
Определить порядок выполнения жоементарных функций и заполнить ими заголовки столбцов
Выполнить элементарные функции для каждого набора переменных
Вычислить окончательное значение функции в окончательном наборе
Пример:
Построить таблицу истинности для следующей функции:
_
F = A + B · C
A |
B |
C |
_ C |
B · C |
_ F = A + B · C |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
Пример:
Посмтроить таблицу истинности для следующей функции:
_ _
F = (A + B)&(B + C)
A |
B |
C |
_ B |
_ A+B |
_ C |
_ B+C |
_ _ F = (A + B) & (B + C) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
Алгебра логики и её законы
1) Закон одинаковости:
A + A = A
A & A = A
2) Закон коммутативности :
A + A = B + A
A & A = B & A
3) Закон ассоциативности :
A + (B + C) = (A + B) + C = B + (A + C)…
A · B · C = (B · C) · A = (C · A) · B…
4) Закон дистрибутивности:
A · (B + C) = A · B + A · C
A + B & C = (A + B)(A + C)
5) Закон двойного отрицания:
=
A = A
6) Закон Де Моргана:
_ _ ____ _ _ ____
A + B = (A & B) A + B = (A + B)
7) Законы поглощения:
A + A & B = A
A & (A + B) = A
8) Законы определения действий с логическими константами 0 и 1
A + 0 = A A + 1 = 1
A · 0 = 0 A · 1 = A
_ _
0 = 1 1 = 0
_ _
A + A = 1 A · A = 0
9) Законы Блейка - Порецкого :
_
A + A · B = A + B
_ _
A + A · B = A + B
_ _ _
A + A · B = A + B
_ _ _ _
A + A · B = A + B
Пример 1:
(A + B) · (A + C) = A · A + A · C + B · A + B · C = A + A · B + B · C = A (1 + C) + A · B + B · C = A + A · B + B · C = A (1 + B) + B · C = A + B · C
Пример 2:
_ _ _ _ _ _ _ _ _
F = A · B + A · B + A · B + A · C = B (A + A) + A · B + A · C = B + A · B + A · C = A + B + A · C = B + A + A · C = B + A(1 + C) =
_
= A + B
Пример 3:
По заданной функции: а) построить ТИ
Б) упростить
F
= A · (
)
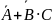А)
A |
B |
C |
_ A |
B · C |
_ A + B · C |
|
F = A · ( ) |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
Б)
F = A · ( )
Упростим отдельно скобку:
_
Пусть A = X
И пусть B · C = Y
Тогда:
=
=
·
=
·
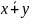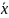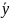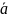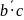= a · (
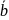· c) = a · (
+
)
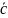F = a · (a · ( + )) = a · ( + )