2.1 Метод последовательного синтеза

Сущность метода последовательного синтеза сводится к следующему: исходную систему уравнений (1.24) представим в скалярном виде

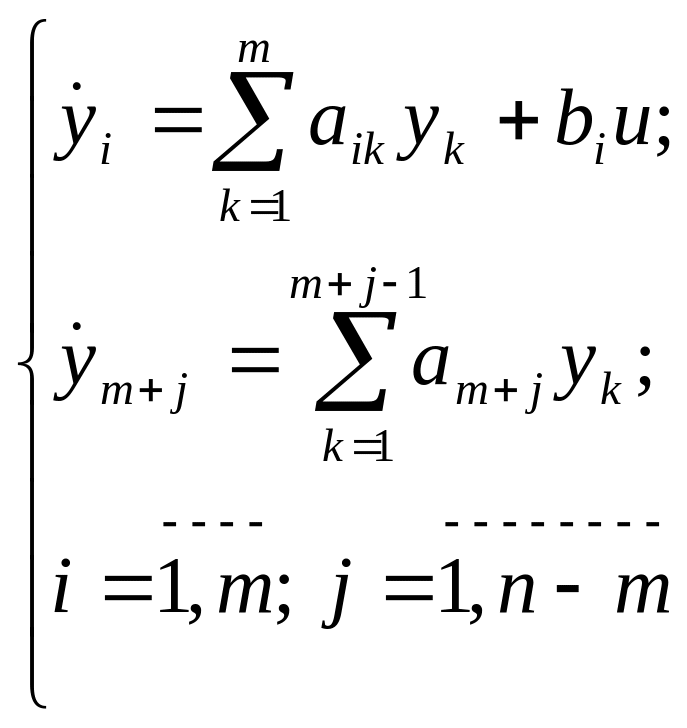(1.32)

где y_i — координаты системы; u_i — управляющие воздействия, которые отыскиваются в виде u_i=u_maxsign σ; u_max ≤u_ДОП. Пусть L_m — область управляемости для системы Y^m. Тогда если синтезировано оптимальное по быстродействию управление для первого уравнения системы (1.32), а u_m(y₁,y₂,…,y_m) и φ_k^um(y₁,y₂,…,y_m) (k=1,n) есть траектория, ведущая из области управляемости y₁…y_m (D_m) в начало координат, то оптимальное по быстродействию управление для системы (m+1) порядка с точностью до знака будет

(1.33)

Управление (1.33) переводит в начало координат только те точки системы (1.32) из области L_m+1 которые подчинены условиям

(1.34)

Соотношение (1.34) представляет собой уравнение поверхности переключения системы σ(y₁,y₂,…,y_m+1) и позволяет строить достаточно полную сетку точек, лежащих на этой поверхности. Вычислительная процедура по построению управления (1.33) выполняется на ЭВМ. Процедура заключается в получении таблицы точек искомой функции σ(y₁,y₂,…,y_m) с числом входов, на единицу меньшим, чем порядок рассматриваемой системы. Необходимым условием реализации вычислительной процедуры является решение на ЭВМ уравнений движения неизменяемой части системы (1.32).

Изложенный метод синтеза нелинейных управлений наряду с преимуществами — выполнением условий tп.п < tдоп, |U(t)|<<|U|доп — имеет ряд недостатков:

1) потребность в приведении исходной матрицы А в (1.24) к треугольной форме; эта операция для плохо обусловленных систем высокого порядка приводит к большим затратам машинного времени;

2) необходимость в реализации процедуры построения поверхности переключения, что связано с нарастанием погрешностей при увеличении размерности системы;

3) в функционале метода отсутствует учет внешних возмущений.

Дадим более общую постановку задачи синтеза с учетом возмущений и выведем управления, обеспечивающие одновременно оптимальность переходного процесса и инвариантность к внешним возмущениям.

Рассмотрим вновь систему (1.24), положив в ней D=E и заменив размерности n₁=n₃=n, m=n₂. Тогда получим систему

, (1.35)

где Y(t) и X(t) — векторы параметров состояний и возмущений порядка n, непрерывные на промежутке [0, ∞]; для всех компонент вектора X(t) соблюдается условие N<|x_i(t)|<.M, N и М — заданные константы; U — вектор-функция управлений порядка m; А и В —матрицы постоянных коэффициентов порядков (nxn) и(nxm) соответственно.

В (1.35) все матрицы и векторы вещественные; предполагается, что пара (А,В) управляема, т. е. среди столбцов матрицы ||В,АВ,…, А^n-1В|| есть n линейно независимых. В качестве функционала, обеспечивающего инвариантность системы (независимость от возмущений), принимается функционал вида

, (1.36)

где Р — матрица знакопеременных коэффициентов размера nxn;

.

С помощью этой матрицы обеспечивается положительность подынтегральной функции (1.36); R_x — положительная диагональная матрица весовых коэффициентов порядка (mxm). Вектор U_x (порядка m) называется управлением по возмущению и является составляющим вектора общего управления U, причем U =U₀+U_x. В случае |x_i(t) | ≤N U_x=0.

Составляющая общего управления U0, обеспечивающая оптимальное демпфирование переходных процессов и синтезируемая по квадратичному критерию качества

,

определяется известным образом:

, (1.37)

где К — положительно-определенная симметричная матрица, которая отыскивается из решения уравнения Дж. Риккати (итальянский математик, 1676—1754)

. (1.38)

В этом уравнении Q, R— заданные положительно-определенные матрицы, вычисляемые в соответствии с критериями качества(1.8), (1.9); A^T, В^T — транспонированные матрицы A, В.

Уравнение (1.38) решается путем численного интегрирования дифференциального уравнения . Для определения Ux будем использовать классический метод Лагранжа, считая, что U₀ уже найдено. В этом случае систему (1.33) можно записать в виде

, (1.39)

где S = A-BR^-1B^TK — матрица Гурвица, т. е. матрица, собственные числа которой расположены в левой полуплоскости комплексной переменной p уравнения |pЕ-A|=0.

Для функционала (1.36) и системы (1.39) напишем функцию Гамильтона:

, (1.40)

где ψ — вектор-функция с элементами ψ₁,ψ₂,…,ψ_n причем ψ₀=Е. Векторная функция ψ(t) удовлетворяет системе уравнений Эйлера- Лагранжа:

. (1.41)

Применяя к выражению (1.40) правило векторного дифференцирования, получим следующее векторное уравнение для функции ψ:

. (1.42)

Согласно условию стационарности функции H, можно записать

. (1.43).

Из уравнения (1.43), полагая, что матрица R_x невырожденная, получим

. (1.44)

В результате приходим к системе дифференциальных уравнений, из решения которой определяется искомая функция ψ:

. (1.45)

В аналитическом виде после решения уравнений (1.45) управление (1.44) можно представить в форме

, (1.46)

где матрица Р, являющаяся матрицей знакопеременных коэффициентов, вычисляется в процессе решения системы (1.45).

Таким образом, общий нелинейный закон управления можно представить в виде

, (1.47)

Согласно алгоритму машинного синтеза САУ (см. рис. 3), следующим этапом после определения структуры и начальных параметров регулятора является параметрическая оптимизация регулятора машинно-аналитическим методом, который включает в себя процедуры оптимального поиска.

Такие процедуры сводятся в общем случае к задачам нелинейного программирования. При применении известных методов нелинейного программирования, которые достаточно хорошо разработаны лишь для случаев выпуклого и, в частности, квадратичного программирования, оптимизация параметров САУ осложняется наличием дополнительных условий и ограничений, а в ряде случаев— необходимостью поиска экстремума.

Перечислим специфические свойства, присущие целевым функциям в процедурах поиска при оптимизации параметров САУ:

- характеристики качества, даже для линейных систем зависят от параметров поиска нелинейно;

- целевая функция — неявная функция своих аргументов, как правило, имеет локальные экстремумы, «гребни», «овраги» и т. д.

Отсюда следует невозможность выбора какого-либо одного метода поиска, «справляющегося» со всеми перечисленными особенностями целевых функций. Достаточно удобен поиск оптимальных параметров V, К при синтезе управлений U (рис. 3) в САУ на основе моделирования. В этом методе применяются два подхода: программный подход, когда исследователь по заранее составленной программе изменяет параметры V, К, «отслеживая» изменения показателя качества, и автоматический синтез с помощью оптимизатора, реализованного либо аппаратно, либо программно.

При наличии у исследователя определенного опыта и интуиции первый подход во многих случаях приводит к успеху при решении сложных задач. Естественно, что при этом должна быть достаточно совершенной методика моделирования.

Остановимся подробнее на втором подходе в случае аппаратной реализации алгоритмов оптимизации на АЦК, в составе которых имеются специальные «оптимизаторы». Принцип действия такого оптимизатора следует из рис. 4. В оптимизаторе аппаратно средствами аналого-цифровой техники реализуется один из критериев качества :

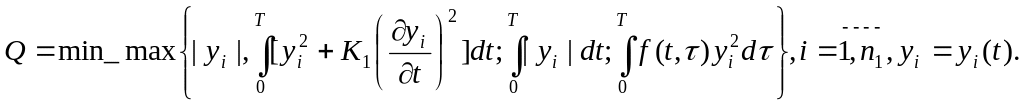
Исходная система уравнений (3.10) Y’=F(Y, X, U, Δ, t) решается многократно. В период времени между «пуском» и «остановкой» АВМ производится решение системы (3.10) при фиксированном варианте изменяемых параметров: V^(k), K^(k).

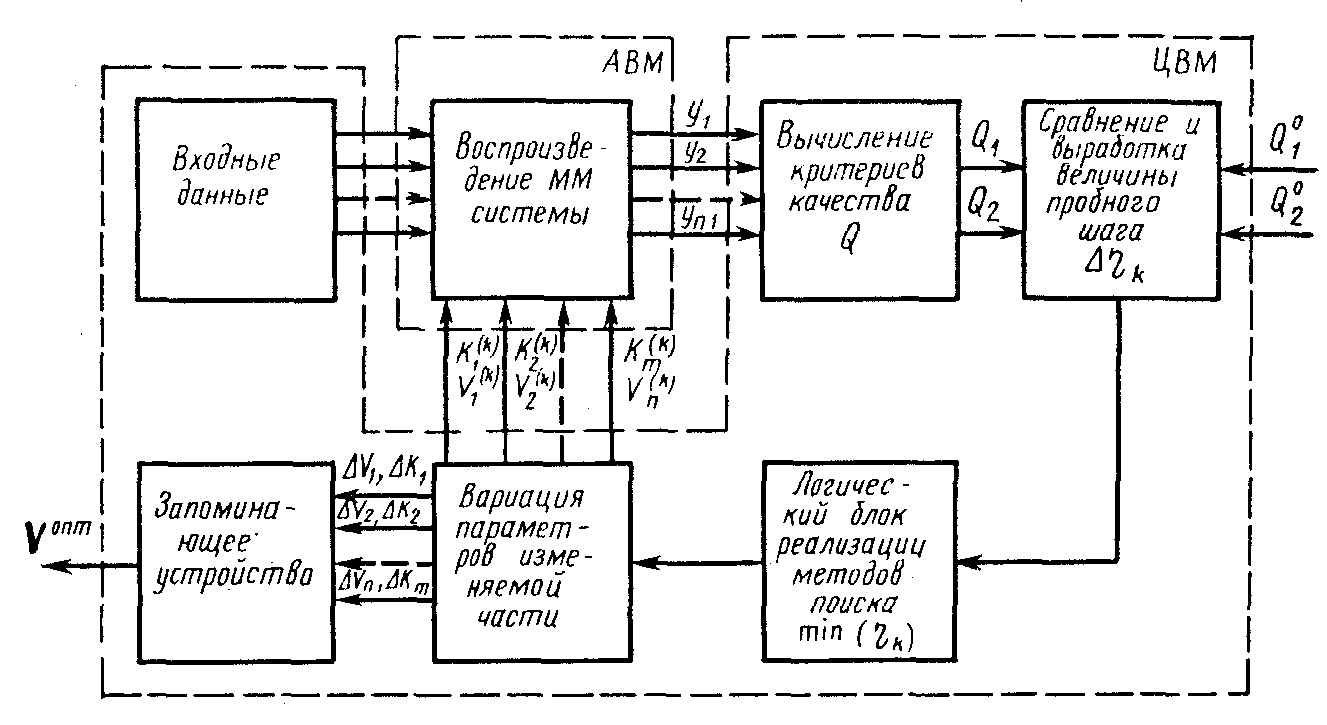
Рис. 4. Схема работы «оптимизатора» на АЦК

В период между «остановкой» и «возвратом к исходному положению» производится вычисление основных и дополнительных критериев качества и их отклонений от желаемых (установленных на оптимизаторе) значений Q₁⁰, Q₂⁰:

,

где К_M — задаваемый масштаб.

Вычисляется шаг поиска минимума величины

где a_i, a_2j — весовые коэффициенты.

В период между «возвратом к исходному положению» и новым «пуском» осуществляется изменение

.

При этом очередные значения V^(k), K^(k) фиксируются в запоминающем устройстве и по окончании поиска, когда

выдаются в виде конечного результата.