3.1.4. Табличный симплекс-метод

Рекомендуется следующий порядок решения задачи ЛП с использованием табличного симплекс-метода:

1. Математическая модель задачи приводится к расширенной форме.

2. Определяется начальное базисное допустимое решение.

3. Составляется исходная симплекс-таблица (табл.3.1), в которую вносятся следующие параметры, соответствующие начальному базисному допустимому решению:

3.1. Весовые коэффициенты при переменных целевой функции (строка С).

3.2. Весовые коэффициенты целевой функции при базисных переменных (столбец С).

3.3. Переменные , которые входят в текущий базис (столбец Х_Р).

3.4. Свободные коэффициенты уравнений ограничений (столбец В).

3.5. Элементы матрицы условий задачи (столбцы А₁, А₂,…,А_n).

Таблица 3.1

С			c1	…	cj	…	ck	…	cn
	ХP	B	A1	…	Aj	…	Ak	…	An
c1	x1	b1	a11	…	a1j	…	a1k	…	a1n
…	…	…	…	…	…	…	…	…	…
ci	xi	bi	ai1	…	aij	…	aik	…	ain
…	…	…	…	…	…	…	…	…	…
cr	xr	br	ar1	…	arj	…	ark	…	arn
…	…	…	…	…	…	…	…	…	…
cm	xm	bm	am1	…	amj	…	amk	…	amn
S			S1	…	Sj	…	Sk	…	Sn

3.6. Симплекс-разности S_j ( (последняя строка).

Симплекс-разности вычисляются по формуле (3.17)

где с_iвесовые коэффициенты при базисных переменных.

Из (3.17) следует, что коэффициенты z_j вычисляются для каждого столбца как сумма почленных произведений коэффициентов с_i на одноименные коэффициенты j-го столбца. Например:

Примечание. При заполнении симплекс-таблицы (в дальнейшем для определенности будем рассматривать задачу максимизации целевой функции) необходимо иметь в виду:

если для всех , то полученное базисное решение является оптимальным;

если имеются и в столбцах А_j, соответствующих этим симплекс-разностям, существует хотя бы один элемент то возможен переход к новому решению, связанному с большим значением целевой функции;

если имеются и в столбцах А_j все элементы то в области допустимых решений целевая функция не ограничена сверху.

4. Определяется вектор А_k, который необходимо ввести в базис для улучшения решения, по наибольшему значению симплекс-разности S_k. Переменная этого столбца x_k будет новой базисной переменной, которая вводится в новое базисное решение.

Столбец, содержащий эту симплекс-разность, называется направляющим столбцом.

5. Определяется вектор, который нужно вывести из базиса, используя равенство

(3.18)

Условие (3.18) позволяет найти направляющую строку. Переменная x_r , соответствующая этой строке, выводится из базисного решения и заменяется переменной x_k направляющего столбца. Элемент a_rk , который стоит на пересечении направляющего столбца и направляющей строки, называется направляющим элементом.

6. Заполняется таблица, соответствующая новому базисному решению. В этой таблице прежде всего заполняются клетки строки x_r с вводимой переменной x_k. Для этого все элементы этой строки делятся на направляющий элемент. Получаются элементы новой строки:

(3.19)

Остальные элементы новой таблицы определяются по формулам исключения (на основании метода полного исключения Гаусса):

(3.20)

где ,  новые элементы последующей таблицы; a_rk  направляющий элемент.

Для практических расчетов необходимо иметь в виду следующее:

в новой таблице на месте направляющего элемента пишется I, а на месте остальных элементов направляющего столбца  нули;

если в направляющей строке (старой таблицы) окажется 0, то соответствующий ему столбец переписывается в новой таблице без изменений;

если в направляющем столбце (старой таблицы) окажется 0, то соответствующая ему строка переписывается в новой таблице без изменений.

Процесс вычисления заканчивается, когда найдено оптимальное решение (см. примечание п.3.6).

В случае, когда требуется решать задачу на минимум целевой функции, целесообразно ее привести к задаче на максимум путем умножения всех коэффициентов целевой функции на (1). После такого преобразования алгоритм решения задачи остается прежним.

Пример 3.4. Найти максимум целевой функции

при ограничениях

Запишем ограничения в расширенной форме:

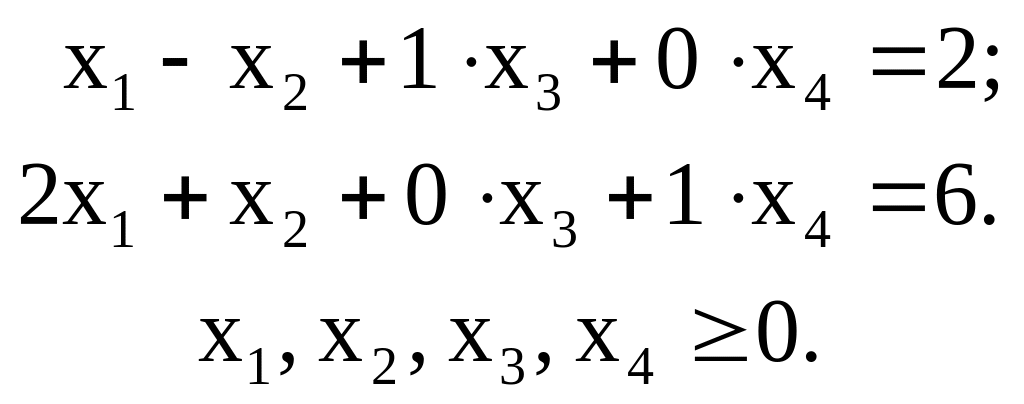
Обозначим векторы условий задачи А₁А₄.

Векторы А₃, А₄ образуют единичную матрицу, которую примем за базис. В результате начальное базисное допустимое решение будет иметь вид Х (0,0,2,6).

Составим исходную таблицу, в которой элементы строки S рассчитываем по формуле (3.17) (см. табл. 3.2).

					↓	Таблица 3.2
	С				с1	с2	с3	с4
					3	2	0	0
			ХP	B	A1	A2	A3	A4
←	с3	0	x3	2	1	-1	1	0
	с4	0	x4	6	2	1	0	1
	S			0	3	2	0	0

В индексной строке табл.3.2 имеются , что позволяет улучшить решение задачи.

Введем в новый базис вектор А₁, которому соответствует наибольшее значение симплекс-разности S₁=3. Этот столбец будет направляющим (в табл. 3.2 указан стрелкой ↓).

Составим отношения вида , по которым определим направляющую строку. Для этого находим

Итак, направляющая строка первая (указана стрелкой ←), направляющий элемент а₁₁ (в табл.3.2 заключен в прямоугольник).

Рассчитаем и заполним новую таблицу, соответствующую новому базисному решению, пользуясь п.6 рекомендованного порядка и формулами (3.20).

						↓ Таблица 3.3			Для пояснения приведем несколько элементов табл.3.3: Примечание. Индексы коэф- фициентов, характеризующих но-
	С				с1	с2	с3	с4
					3	2	0	0
			ХP	B	A1	A2	A3	A4
	c1	3	x1	2	1	-1	1	0
←	c4	0	x4	2	0	3	-2	1
	S			6	0	5	-3	0

мер строки, соответствуют индексам базисных переменных.

В индексной строке табл. 3.3 имеется S₂ с положительным знаком, что позволяет продолжить улучшение решения задачи.

Из табл. 3.3 определяем направляющий столбец и направляющую строку (столбец  второй, строка  вторая).

Последующие результаты расчета сведены в табл. 3.4, 3.5.

				Таблица 3.4								Таблица 3.5
С			с1	с2	с3	с4		С			с1	с2	с3	с4
			3	2	0	0					3	2	0	0
	ХP	B	A1	A2	A3	A4			ХP	B	A1	A2	A3	A4
c1	x1		1	0				c3	x3	8	3	0	1	1
c2	x2		0	1				c2	x2	6	2	1	0	1
S			0	0				S		12	-1	0	0	-2

В табл. 3.5 все Поэтому полученное решение является оптимальным: