3.3. Задачи нелинейного программирования

3.3.1. Общие сведения

Общая задача нелинейного программирования (НП) формулируется следующим образом: найти решение Х=(х₁, х₂, … , х_n), доставляющее максимум (минимум) целевой функции

F(X)=f(х₁, х₂, … , х_n) (3.27)

при ограничениях

(3.28)

Функции F(X) и g_i(X) (i= ) в общем случае нелинейны. Знаки ограничений (3.28) могут быть и другими, а также быть равенствами. Условия неотрицательности переменных x_j (j= ) в задачах НП обычно включаются в ограничения (3.28).

Г

25

еометрическое представление задач НП показывает, что их решение может находиться как на границе области допустимых решений, так и внутри этой области. Целевая функция в области допустимых решений, кроме глобального экстремума, может иметь несколько локальных экстремумов.

3.3.2. Квадратичное программирование

Модель задачи квадратичного программирования имеет вид

(3.29)

при ограничениях

, (3.30)

. (3.31)

Второе слагаемое (3.29) называется квадратичной формой переменных х₁, х₂, … х_n. В задачах квадратичного программирования определение глобального экстремума связано с выпуклостью (вогнутостью) целевой функции. Выпуклость (вогнутость) целевой функции определяется квадратичной формой, а выпуклость (вогнутость) квадратичной формы зависит от того, является ли она положительно (отрицательно) определенной или положительно (отрицательно) полуопределенной.

Принадлежность квадратичной формы к одному из указанных видов можно установить по знакам определителей матрицы D= :

.

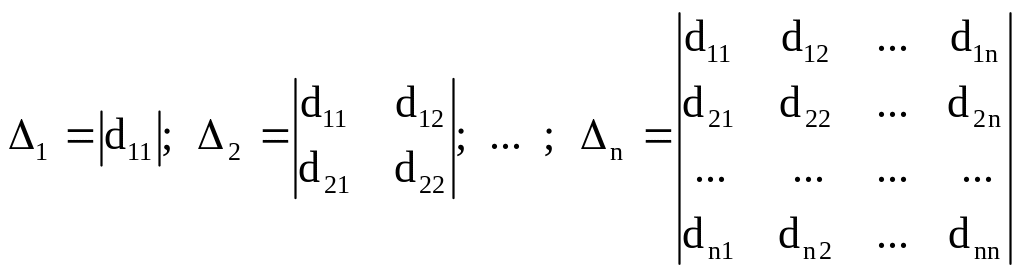Матрица D предполагается симметричной (d_kj=d_jk). Диагональные элементы d_kk этой матрицы являются коэффициентами при , а недиагональные элементы d_kj=d_jk равны половине коэффициента при х_kx_j.

В соответствии с изложенным можно получить следующие утверждения:

1. Если все определители положительны, то квадратичная форма будет положительно определенной.

2. Если в ряду чисел знаки чередуются, то квадратичная форма будет отрицательно определенной.

3. Если ранг матрицы D равен r<n, то квадратичная форма будет положительно полуопределенной, если первые r определителей положительны, а остальные равны нулю.

4. Если ранг матрицы D равен r<n, а в ряду чисел знаки чередуются и , то квадратичная форма будет отрицательно полуопределенной.

Пример 3.6. Определить вид квадратичной формы

.

Составим матрицу D и найдем ее определители:

.

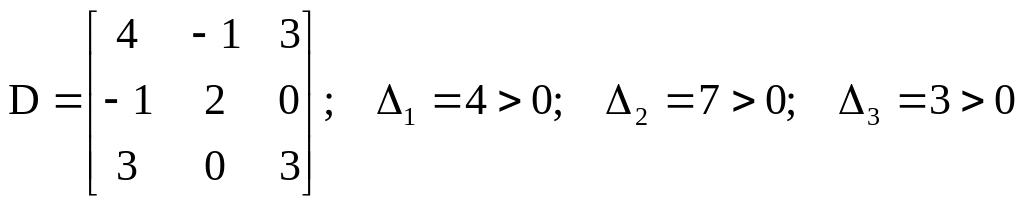Все определители положительны, поэтому квадратичная форма является положительно определенной, т.е. выпуклой.

Решение задачи квадратичного программирования основано на применении условий Куна-Таккера. При этом функция Лагранжа записывается в виде

(3.32)

или в матричной форме

(3.33)

Путем преобразования условий Куна-Таккера, используя дополнительные переменные, задача (3.29) – (3.31) сводится к задаче ЛП. В результате получается задача максимизации псевдоцелевой функции

(3.34)

при условиях

. (3.35)

. (3.36)

(3.37)

Можно использовать следующий порядок решения задачи квадратичного программирования:

1. Составляется функция Лагранжа.

2. Записываются условия Куна-Таккера.

3. Используется метод искусственного базиса с применением математической модели (3.34) - (3.37).

4. Находится оптимальное решение при выполнении условий (3.36).

Пример 3.7. Найти решение задачи квадратичного программирования

(3.38)

при ограничениях

(3.39)

Поскольку (при d₁₂ d₂₁ -1 и d₂₂ -2), то функция (3.38) – вогнута.

Составим функцию Лагранжа

Запишем условия Куна-Таккера

, (3.40)

(3.41)

Систему линейных неравенств (3.40) перепишем в виде

. (3.42)

Приведем неравенства (3.42) к равенствам, используя дополнительные переменные v₁, v₂ и w₁

(3.43)

Дополним равенства (3.43) условиями (3.41), которые представим в виде

v₁x₁=0; v₂x₂=0; w₁₁=0. (3.44)

Найдем базисное допустимое решение системы (3.43) с учетом равенств (3.44). Для этого воспользуемся методом искусственного базиса, вводя искусственные переменные z₁ и z₂ в уравнения системы (3.43). В результате получим задачу ЛП:

максимизировать (3.45)

при условиях

(3.46)

Решим задачу (3.45) – (3.46) табличным симплекс-методом, учитывая дополнительные ограничения (3.44) на выбор базиса.

В табл. 3.7 и 3.8 отображены соответственно начало и результат решения задачи.

Таблица 3.7

С			0	0	0	0	0	-M	-M	0
	Xp	A0
-М	z1	4	4	2	1	-1	0	1	0	0
-М	z2	6	2	4	2	0	-1	0	1	0
0	w1	2	1	2	0	0	0	0	0	1
S			6M	6M	3M	-M	-M	0	0	0

Таблица 3.8

С			0	0	0	0	0
	Xp	A0
0	x1		1	0	0
0	1	1	0	0	1	0
0	x2		0	1	0
S			0	0	0	0	0

В табл. 3.8 получено оптимальное решение, удовлетворяющее условиям (3.44): .

Примечание. В случае, когда некоторое из условий (3.36) оказывается нарушенным, например v_jx_j0, или w_j_i0, где j – индекс конкретной переменной, необходимо перейти к определению следующего базисного допустимого решения. Для этого из полученного базисного решения необходимо вывести одну из переменных v_j, x_j, w_j или _j и выполнить следующую итерацию.

Графическое решение задачи можно выполнить по методике, изложенной в [4] с. 133-134, или построить линию равного уровня целевой функции (3.38) для значения F(X)=F_max(X) и определить ее положение относительно области допустимых решений, соответствующей ограничению (3.39).