3.1.2. Графический метод решения задачи лп

Графический метод основан на геометрической интерпретации задачи ЛП. Рассмотрим ограничения (3.2) в виде равенств и будем исходить из того, что число переменных n на два больше числа независимых уравнений ограничений m, т.е. n-m=2. Тогда две из переменных, например х₁ и х₂, можно принять в качестве свободных, а остальные m сделать базисными и выразить их через свободные. В результате получим m n-2 уравнений вида

(3.13)

где и - сочетания коэффициентов a_ij и b_i соответственно.

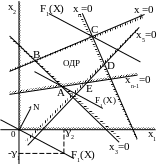
Будем искать решение задачи на плоскости в прямоугольной системе координат х₁0х₂ (рис.3.1).

Допустимые решения для переменных х₁ и х₂ будут находиться выше оси 0х₁ и правее 0х₂, что отмечено на рис.3.1 штриховкой одной из сторон этих осей.

Найдем на плоскости х₁0х₂ отображения остальных переменных х₃, х₄, … , х_n в соответствии с выражениями (3.13). С этой целью рассмотрим, например, переменную х₃ и положим, что ее величина равна своему крайнему значению, т.е. х₃=0. Тогда из первого уравнения системы (3.13) получим

Рис.3.1 (3.14)

Это уравнение прямой, на которой х₃=0. Заштрихованная сторона этой прямой соответствует х₃>0.

Аналогично строятся и остальные ограничивающие прямые х₄=0, х₅=0, … , х_n=0, для каждой из которых определяется сторона, где х₄>0, x₅>0, … , x_n>0. Часть плоскости х₁0х₂, заштрихованная область ABCDE называется областью допустимых решений (ОДР). В этой области значения всех переменных положительны, т.е. x_j>0 ( ). Вершины многоугольника ABCDE (крайние точки) называются базисными допустимыми решениями.

Для нахождения оптимального решения подставим (3.13) в (3.1) и после приведения подобных членов получим

. (3.15)

Запишем вместо (3.15) функцию

. (3.16)

Обе функции (3.15) и (3.16) достигают максимума (минимума) при одних и тех же значениях х₁ и х₂.

Найдем значения х₁ и х₂, доставляющие максимум (минимум) функции F₁(X). Для этого определим положение этой функции на плоскости х₁,х₂ (рис. 3.1).При F₁(X)=0 из (3.16) следует, что эта функция есть прямая, проходящая через начало координат. Вторая точка, через которую пройдет эта прямая, определяется координатами ; . Если функции F₁(X) придавать различные постоянные значения, то прямая на рис. 3.1, отображающая эту функцию, будет перемещаться параллельно самой себе. Причем при положительности коэффициентов и направление N возрастания F₁(X)  вверх и направо (убываниявниз налево). При других значениях и направление возрастания (убывания) функции меняется. Очевидно, максимального значения функция достигнет, когда прямая F₁(X) достигнет крайней точки С области допустимых решений. Координаты этой точки и определяют оптимальное решение . Зная и и пользуясь (3.13), определяют

Точка А области допустимых решений будет соответствовать минимуму функции F₁(X).

Пример 3.1. Найти решение Х=(х₁, х₂), доставляющее минимум целевой функции

F(X)=3x₁3x₂

при ограничениях

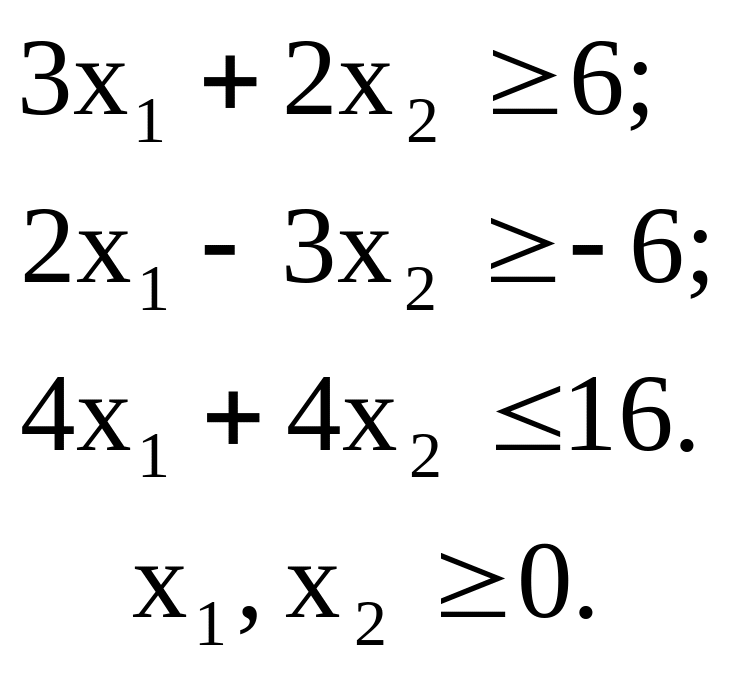
Ограничения приведем к равенствам, используя дополнительные переменные х₃, х₄, х₅:

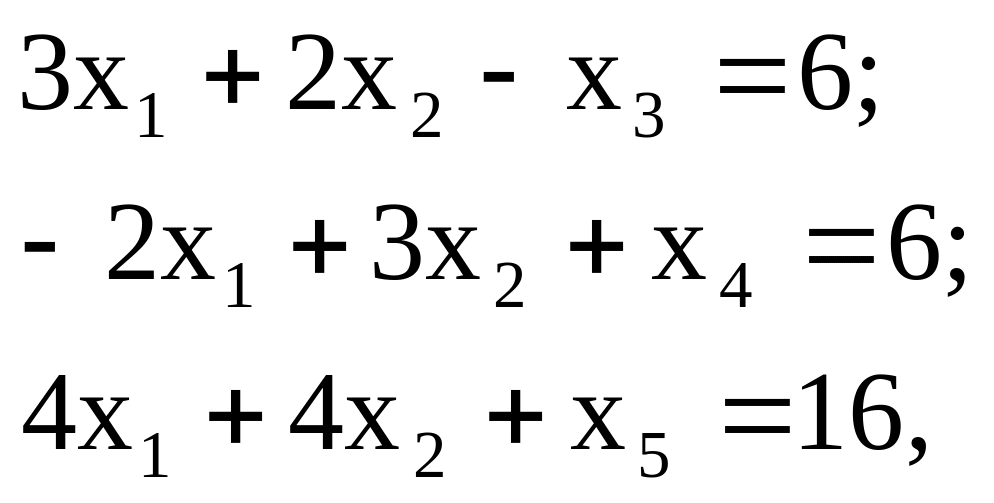
о

х₄=0

ткуда

х₂

2

3

4

B

C

F(X)

-2

-2

-1

х₁

х₃=0

х₅=0

1

2

3

4

5

1

-1

N

A

D

ОДР

-3

Прямые, соответствующие граничным значениям переменных х₃=х₄=х₅=0, представлены на рис.3.2. Заштрихованная область ABCD будет областью допустимых решений.

Рис.3.2

В

9

ектор N показывает направление параллельного перемещения функции F(X), соответствующее уменьшению целевой функции. Минимального значения целевая функция достигает в крайней точке В многоугольника ABCD. Координаты точки В будут оптимальным решением задачи При этом