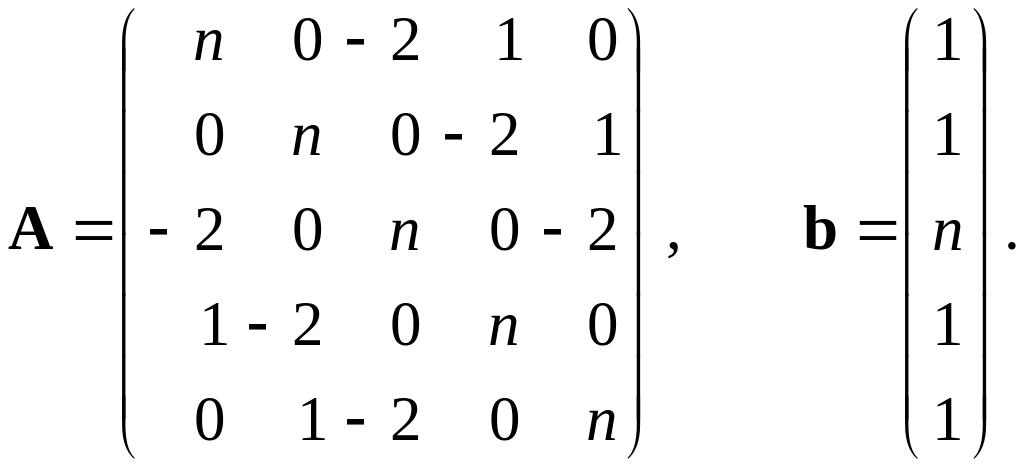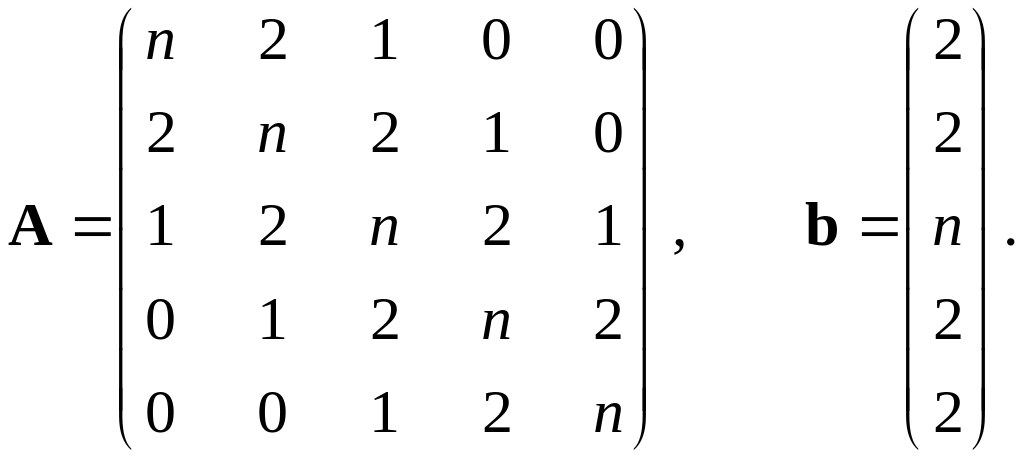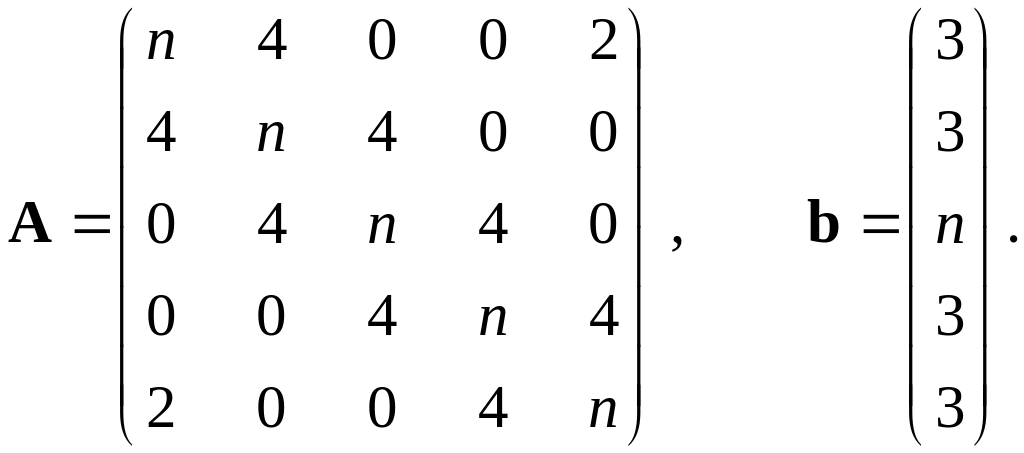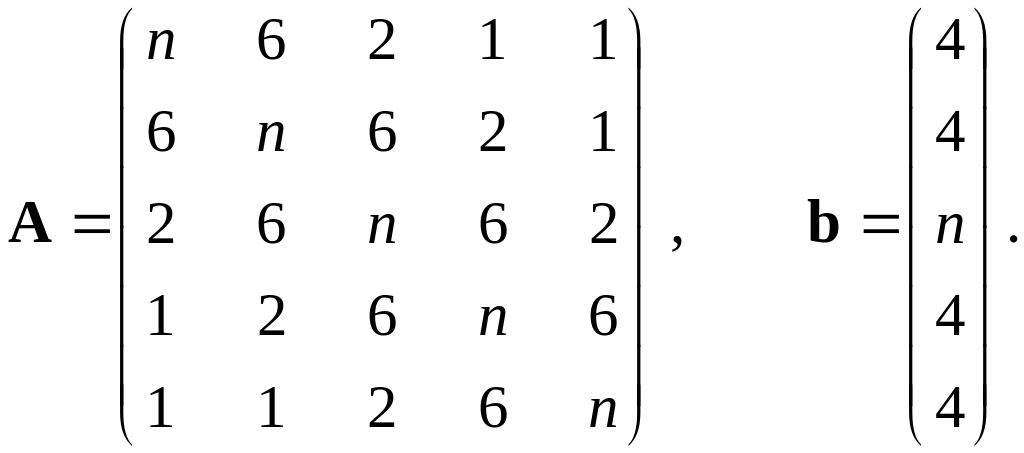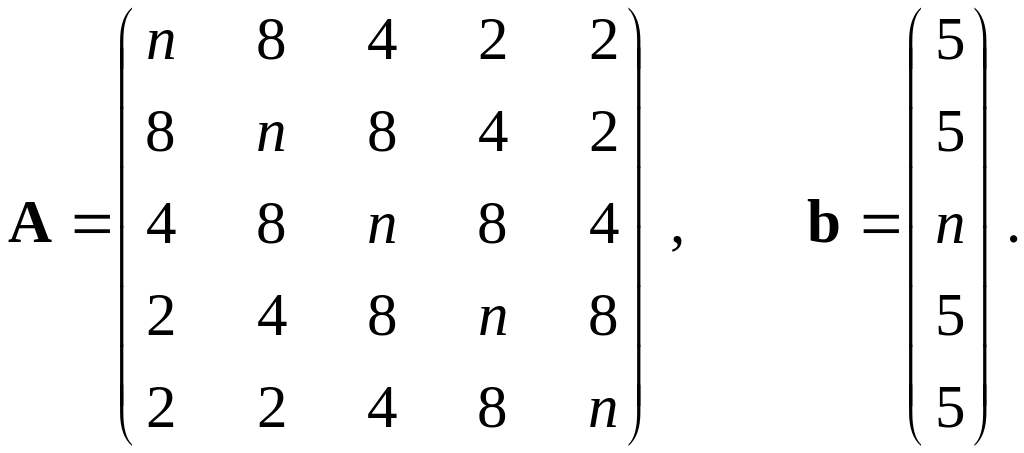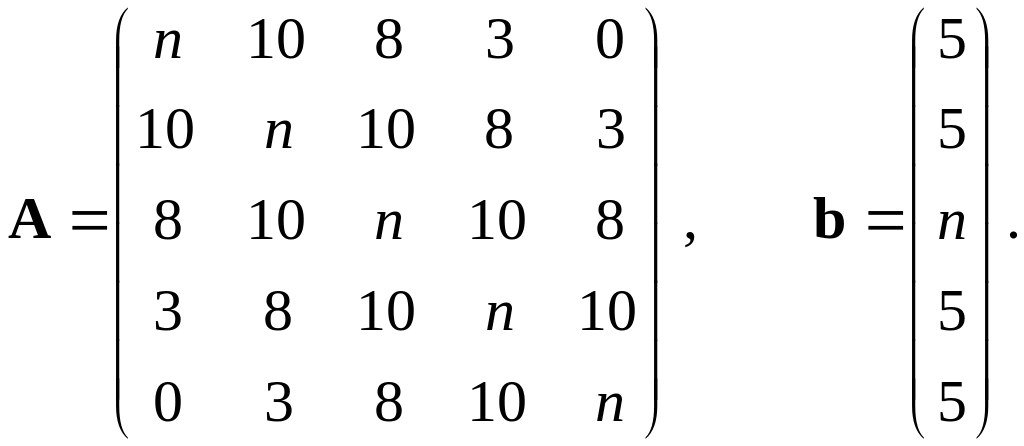Программное обеспечение Excel’а

Для решения систем линейных алгебраических уравнений общего вида в программе Excel имеется стандартная функция МОБР, которая позволяет находить обратную матрицу A^–1 исходной системы. С помощью обратной матрицы, которая при умножении на матрицу системы даёт единичную матрицу, вектор решения системы будет . При этом для умножения матриц в программе Excel есть стандартная функция МУМНОЖ.

Для правильного отображения результатов работы функций МОБР и МУМНОЖ после ввода параметров необходимо нажать комбинацию клавиш «Shift+Ctrl+Enter».

Ниже на рис.3 приведена реализация описанного способа решения в рамках программы Excel системы уравнений

.

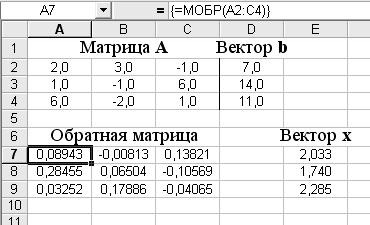
Рис.3.

Контрольные задания

Найти решение системы линейных алгебраических уравнений . Для этого реализовать один из описанных в работе методов. Выбор итерационных методов решения систем должен быть обоснован предварительной проверкой матрицы системы на условие сходимости. В случае применения итерационных методов принять относительную разницу между соседними приближениями вектора решения не более чем 0.000001. Оценить относительную погрешность полученного решения. Матрицу А и вектор b взять по номеру своего варианта, заменяя значение n номером своего варианта.

1–5.

6–10.
11–15.
16–20.
21–25.
26–30.

4. Интерполяция таблично заданных функций Справочная информация

Интерполяцией называется приближение функции, значения которой заданы в виде таблицы, некоторой другой функцией, которая имеет аналитическое описание и которая совпадает с исходной при табличных значениях аргумента.

Простейшая задача, приводящая к интерполяции функций, заключается в следующем. В дискретные моменты времени x₁, x₂,..., x_n измеряется значение некоторой физической величины y, то есть наблюдается зависимость функции y от аргумента x, и строится таблица

x	x1	x2	...	xn
y	y1	y2	...	yn

По этой таблице требуется восстановить значения функции при любых других значениях аргумента x из отрезка [x₁, x_n] или подобрать аналитическое выражение для приближающей функции y(x) достаточно простого вида, значения которой совпадали бы с заданными в таблице

.

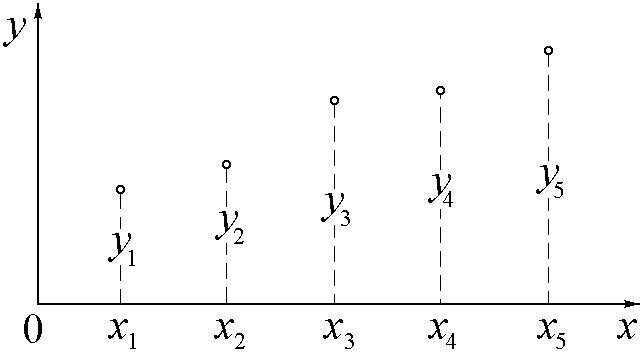Г

Рис.1.

еометрический смысл задачи состоит в том, что через точки, которыми отображаются табличные значения аргумента и функции на поле декартовой системы координат x0y, как это показано на рис.1, и которые называются узловыми точками или узлами интерполяции, необходимо провести, по крайней мере, непрерывную линию, подобрав для неё аналитическое описание.

В зависимости от требований, которые накладываются на приближающую функцию, могут применяться различные формы её представления: линейная, квадратичная, кубическая или более высокого порядка. К простейшим из них относятся кусочно-линейная интерполяция, интерполяция кубическим сплайном и интерполяция многочленами, в частности, многочленом Лагранжа и другие.