2.1.19. Спектры колебаний

В целом ряде практически важных случаев возникает задача о представлении сложного процесса (колебания, волнового движения, излучения, шума и т.д.) в виде набора (суммы) отдельных гармоник с дискретными или бесконечно близкими частотами. Сама операция носит название гармонического (спектрального) анализа, а набор гармоник – спектром (дискретным или непрерывным). Понятно, что каждая гармоника, представляющая собой монохроматическое (одночастотное) колебание входит в спектр не только со своей определенной частотой, но и с амплитудой, и фазой.

В математическом анализе выясняются возможности представления процессов (функций) в виде тригонометрических рядов, т.е. наборов гармоник. Важнейшие результаты в этом направлении были получены Фурье. В частности, он показал, что если процесс является периодическим, но не гармоническим, то он представляется дискретным спектром (рядом Фурье). Более того, если функция, описывающая процесс, является четной, то соответствующий ряд Фурье представляет собой набор косинусоид, а если нечетной – то синусоид. Если функция свойством четности не обладает, то в наборе присутствуют как синусоиды, так и косинусоиды. Если процесс описывается произвольной (непериодической) функцией, то его можно представить в виде непрерывного спектра – интеграла Фурье по частоте. Мы будем рассматривать только периодические процессы, т. е. ряды Фурье. Особенностью разложения Фурье по гармоникам, в основном определяющей его практические применения является то, что в ряде Фурье гармоники низших частот имеют большие амплитуды, чем гармоники более высоких частот, а в сплошном спектре практически всегда можно выделить определенную группу гармоник, амплитуды которых наиболее значительны. Именно такие гармоники определяют энергетику процесса и позволяют не включать в рассмотрение весь бесконечный набор гармоник.

Рассмотрим простейшее сложное колебание – гармонику, модулированную по амплитуде:

x = А cos(ωt -  ) = а(1 + к cos t) cos(ωt -  )= а cos(ωt -  )+ cos((+ω)t -  ) + cos((- ω)t -  ) (118)

Это сложное колебание мы представили в виде набора трех гармоник с несущей частотой ω и двумя боковыми частотами ω+ и ω -. Зависимость амплитуд гармоник от частоты называется амплитудным спектром. Для данного случая он представлен на рис. 29. Начальные фазы у всех наших гармоник одинаковы, т.е. фазы не зависят от частоты гармоник. Если в более сложных случаях такая зависимость появляется, то говорят о фазовом спектре. Например, если гармоническое колебание получено в результате сложения двух одночастотных колебаний со своими амплитудами и фазами, то можно говорить об амплитудном и фазовом спектрах. Заметим, что поскольку гармоническое колебание можно разложить на два (и больше) таких же бесконечным числом способов, то говорить о спектрах отдельных гармоник бессмысленно.

Рассмотрим сложение одночастотных колебаний с одинаковыми амплитудами и равномерно (по линейному закону) нарастающими фазами. Исходные формулы имеют вид (а = ωt, h = φ)

cosa + cos (a + h) +…..+ cos[a + (n-1)h] = ;

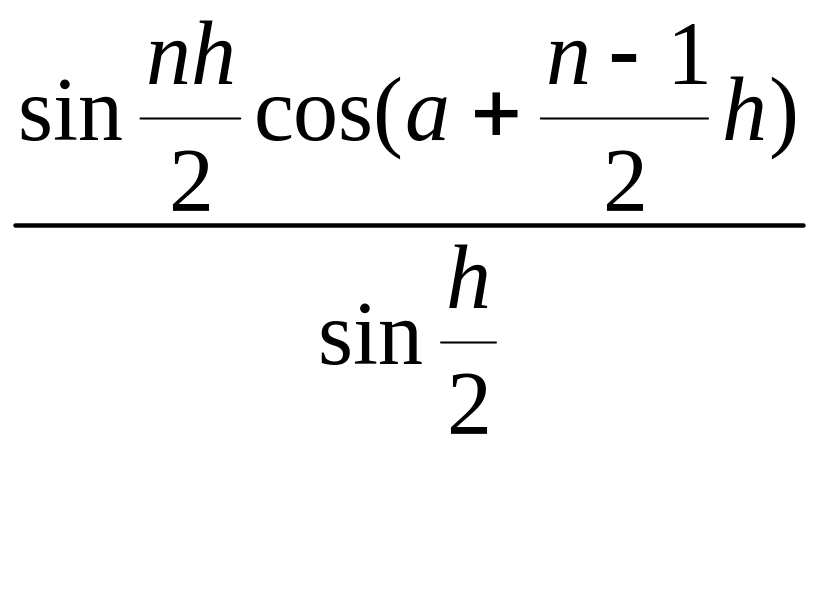sina + sin(a+h) +….+ sin[a + (n-1)h]= . (119)

Здесь амплитуды гармоник стоящих слева одинаковы, а их частоты равноотстоят друг от друга. Следовательно, спектр функций, стоящих справа в (119) представляет собой «гребенку» (см. рис. 30).

Другой пример – гребенка с амплитудами, нарастающими в арифметической прогрессии:

cosa+2cos2a+…..+n cos na = ;

sina + 2sin2a +….+ n sin na = . (120)

Фазовый спектр также может представлять гребенку (рис. 31).

Примеры разложения процессов в ряды Фурье представлены в таблице в /3/. Приведем несколько примеров.

Для четной периодической функции (рис. 32)

f(ωt) = (121)

Для нечетной периодической функции (рис. 33)

f(ωt) = (122)

Для периодической функции, не обладающей свойством четности и заданной на промежутке – π < β t < π функцией x(t) = exp(β t) (рис. 34), имеем ряд Фурье вида

f(ωt)= , (123)

где k – натуральное число.

Спектр затухающей гармоники f(t) = sin(ω₁t) является сплошным и имеет вид:

; (124)

. (125)

Иногда определяют следующие спектральные функции:

- амплитудный спектр

; (126)

- фазовый спектр

. (127)

Все эти спектральные функции для f(t) = A sin(ω₁t) при β = 0,01 с^-1, ω₁ = 10 рад/с представлены на рис. 37 - 40.

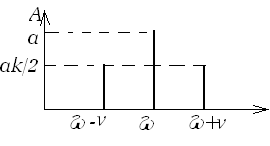
Рис. 29. Амплитудный спектр модулированного по амплитуде колебания

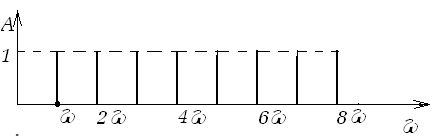
Рис. 30. Дискретный амплитудный спектр «гребенка» (119)

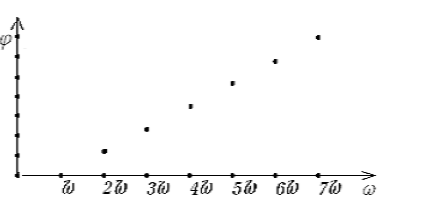
Рис.31. Фазовый спектр «гребенки»

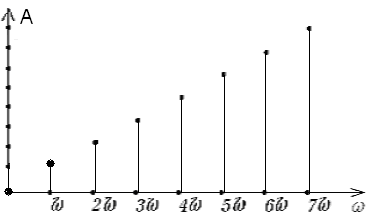
Рис. 32. Дискретный амплитудный спектр (по формуле (120))

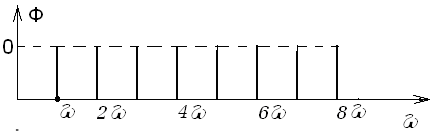
Рис. 33. Равномерный фазовый спектр

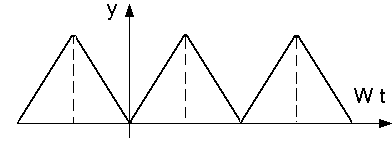
Рис. 34. Четная функция, описывающая колебательный процесс

Рис. 35. Нечетная функция, описывающая колебательный процесс

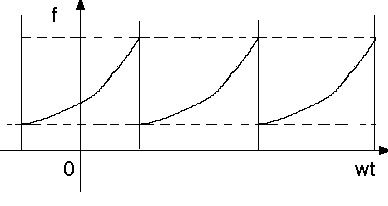
Рис. 36. Колебательный процесс, описываемый функцией, которая не обладает свойством четности

Рис. 37. Косинусный спектр затухающего колебания

Рис.38. Синусный спектр затухающего колебания

Рис.39. Фазовый спектр затухающего колебания

Рис. 40. Амплитудный спектр затухающего колебания

Рис.41. Векторная диаграмма, спектр и вид колебания, являющегося суммой гармоник с одинаковыми амплитудами и фазами, частоты которых нарастают в арифметической прогрессии

При суммировании конечного (или бесконечного) числа гармоник в узком спектральном диапазоне получаются функции, представляющие пакеты. Их часто называют волновыми. Дело в том, что волна, приходя в данную точку пространства, возбуждает в ней колебания. Если в эту же точку в данный момент времени приходят другие волны, то колебания, создаваемые ими, складываются тем или иным образом. Ранее (72 - 73) мы показали, что колебания разных частот можно сложить как колебания одной частоты, но с разными фазами. Наиболее практически важным является случай суммирования гармоник с дискретным набором равноотстоящих частот сосредоточенных в определенном интервале (рис. 41).