2.1.10. Сложение колебаний

Проблема сложения колебаний весьма важна. Пусть тело (материальная точка) имеет возможность совершать колебания вдоль одного направления (колебания с одной степенью свободы). На это тело могут действовать периодические (гармонические) силы с одинаковыми или различными частотами, фазами, амплитудами. Возникает вопрос, каким образом будет двигаться тело, если под действием каждой из сил оно движется независимо. Такая же задача возникает и в случае движения тела в плоскости, в пространстве.

Все подобные задачи имеют важные приложения, например, в теории переходных процессов при установлении вынужденных колебаний, в теории волн, в частности при рассмотрении явлений интерференции и дифракции, в теории поляризации поперечных волн. Несколько волн, приходящих одновременно в заданную точку наблюдения, вызовут в ней колебания, которые будут складываться определенным образом, а мы всегда будем наблюдать лишь результат этого сложения. Наряду с задачей сложения колебаний актуальна задача разложения колебаний на составляющие. Так поляризатор всегда выделяет колебания заданного направления, а спектральный анализатор – колебания определенной частоты.

Итак, сложить колебания - значит сложить движения. Классическим вариантом такой задачи является задача о движении тела, брошенного под углом к горизонту (Физика 9, § 18). Считается, что тело участвует одновременно в двух независимых движениях: равномерном прямолинейном по горизонтали (ось х) и равнопеременном с ускорением g по вертикали (ось у). Изменение координат со временем задается выражениями:

x(t) = v₀cos α₀ t; y(t) = v₀sin α₀ t – 0,5gt² , (70)

где v₀ – скорость, а α₀ – угол бросания.

Исключаем время t из x(t) и подставляем в y(t). Получаем

y(x) = - (1 + tg²α₀)x² + tgα₀ x . (71)

Таким образом, в данном случае сложение движений означает нахождение траектории точки на плоскости х,у.

Сложение гармонических колебаний одинаковой частоты совершаемых вдоль одного направления х:

х₁ = А₁ cos ( ω₁ t + α₁); х₂ = А₂ cos ( ω₁ t + α₂).

Результирующее колебание х = х ₁ + х₂ представим в виде

х = А cos ( ω₁ t + α)

А² = А₁² + А₂² + 2А₁ А₂ cos(α₁ - α₂),

α – вспомогательный угол (см. ниже (73)).

Сложение колебаний разной частоты формально сводится к сложению одночастотных колебаний.

х₁ = А₁ cos ( ω₁ t + α₁); х₂ = А₂ cos ( ω₂ t + α₂).

х = А(t) cos ((А₁ cos α₁ + A₂ cos) + α(t))

с помощью преобразования ₂ - ₁ =   0, ₂ +  t = (t),

приводящего колебание х₂ к виду х₂ = А₂ cos ( ω₁ t + (t) ).

Тогда амплитуда А(t) находится из выражения

А²(t) = А₁² + А₂² + 2А₁ А₂ cos(α₁ - (t)), (72)

Если разность фаз α остается постоянной во времени, то колебания называются когерентными.

При выводе этого соотношения использовано известное математическое тождество:

(А₁ cos α₁ + A₂ cos)cos ω₁ t – (А₁ cos α₁ + A₂ cos) sin ω₁ t =

А cos (ω₁ t + а),

где вспомогательный угол а (в нашем случае зависящий от времени) однозначно находится из соотношений:

cos а = (А₁ cos α₁ + A₂ cos) /А,

sin а = (А₁ sin α₁ + A₂ sin) /А. (73)

Если мы образуем из этих выражений tg а, то дополнительный угол не будет выражаться однозначно.

Полученные соотношения имеют простой геометрический смысл, что позволяет геометрически складывать одночастотные колебания на векторных диаграммах / 1/.

Сложение гармонических колебаний разных частот совершаемых вдоль одного направления х:

Особый интерес представляет случай, когда два скла­дываемых гармонических колебания одинакового на­правления мало отличаются по частоте. Как мы сейчас покажем, результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется б и е н и я м и.

Обозначим частоту одного из колебаний буквой ω, частоту второго колебания через ω + Δ ω. По условию Δ ω ≤ ω. Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Поскольку частоты колеба­ний несколько отличны, всегда можно выбрать начало отсчета времени так, чтобы начальные фазы обоих ко­лебаний были равны нулю. Практически это означает, что мы должны дождаться, пока смещения в обоих ко­лебаниях достигнут одновременно наибольшего поло­жительного значения, и в этот момент «запустить секун­домер». Тогда уравнения обоих

Рис. 16а. Биения и их переменная амплитуда

колебаний будут иметь следующий вид:

x₁ = a cos ωt, x₂ = a cos (ω + Δ ω) t.

Складывая эти два выражения и применяя тригоно­метрическую формулу для суммы косинусов, получаем:

х = x₁+ x₂ = (2a cos ((/2)t)) cos( + Δ ω /2 ) t (74)

(если Δ ω < ω, то во втором множителе пренебрегаем членом Δ ω /2 по сравнению с ω). График функции (74) изображен на рис. 16а. График построен для ω/Δ ω =10. Фазовая траектория биений представлена на рис. 28.

Заключенный в скобки множитель в формуле (74) изменяется гораздо медленнее, чем второй множитель. Ввиду условия  ω < ω за то время, за которое множи­тель соs t совершает несколько полных колебаний, мно­житель, стоящий в скобках, почти не изменится. Это дает нам основание рассматривать колебание (74) как гармоническое колебание частоты , амплитуда ко­торого изменяется по некоторому периодическому за­кону.

Такой подход является весьма продуктивным при изучении сложных колебаний, которые можно описать функцией

x(t) = А(t) cos ( ω₁ t + α₁),

где А(t) - амплитудная функция изменяющаяся со временем гораздо медленнее, чем фаза.

Если складываются однонаправленные колебания разных частот и разных амплитуд, то можно поступить так, как указано в (72). Имеем

x(t) = x₁ (t) + x₂ (t) = А₁ cos ( ω₁ t + α₁) +А₂ cos ( ω₂ t + α₂) = А₁ cos ( ω₁ t + α₁) +А₁ cos ( ω₂ t + α₂)+ (A₂ - А₁ )cos ( ω₂ t + α₂) = 2 A₁cos( )cos( ) +

+ (A₂ - А₁ )cos ( ω₂ t + α₂).

График этой функции представлен на рис. 16 б и является графиком биений. Рис. 16 а иногда называют графиком чистых биений.

Рис. 16 б. График биений – результат сложения колебаний с различными частотами, амплитудами и начальными фазами

Рис. 16 с. Векторная диаграмма сложения разночастотных колебаний

Можно дать геометрическую трактовку сложению разночастотных колебаний. Как следует из рис.16 с , вектор первого колебания строится по обычным правилам, а вектор второго колебания равномерно вращается вокруг конца первого с разностной частотой.

Задача 11.

Сложить два колебания одной частоты, совершаемые по одному направлению:

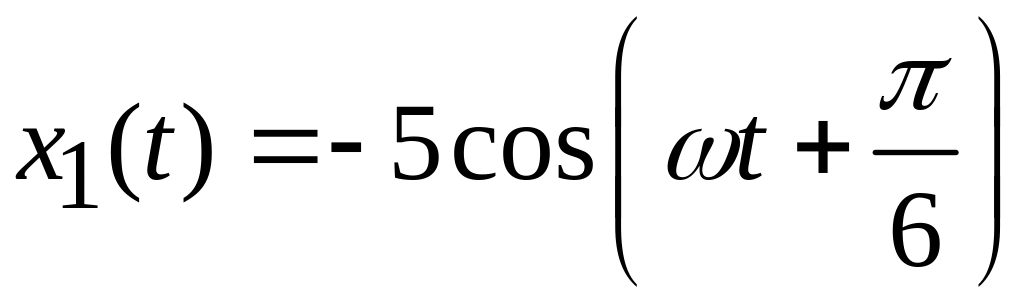; x₂(t) = 2 sin (ωt + 30⁰);

Решение.

Приводим колебания к одному виду описания, через синусы или через косинусы. Для примера, перейдем к косинусам в x₂(t).

; ;

; x₂(t) = 2cos (ωt+ - ) = 2cos(ωt - ).

Уберем знак минус перед амплитудой x₁(t). Этого можно и не делать, достаточно повернуть вектор колебания на π:

x₁ = 5 cos(ωt + π + ) = 5 cos (ωt + ).

Сложим колебания, раскрывая скобки и собирая по отдельности члены, содержащие sin ωt и cos ωt:

Для проверки вычислим угол δ через синус и через косинус:

, ,

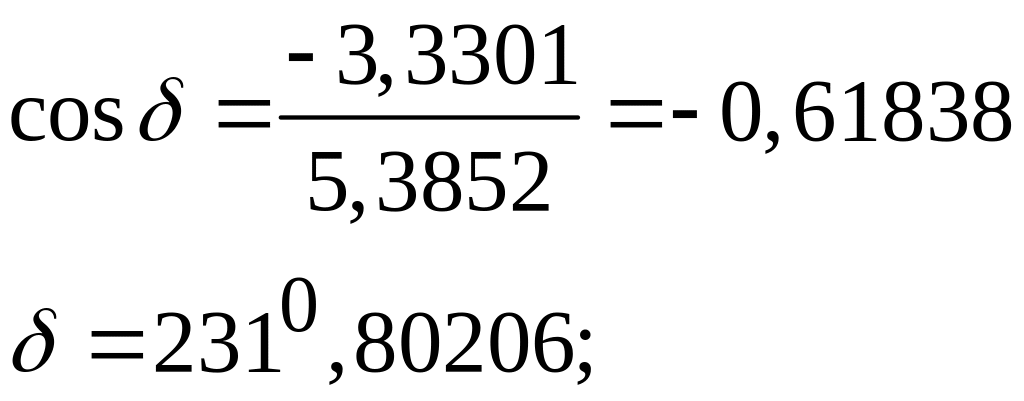231⁰,802 = (231⁰,802 /180⁰).π = 4,046 рад

Ответ: x = 5,38 cos(ωt + 4,046).

На рис. 17 представлена векторная диаграмма сложения указанных колебаний.

Рис. 17. Векторная диаграмма сложения двух одночастотных колебаний ( - произвольный вектор)

Сложение разнонаправленных колебаний. Сложить колебания, совершаемые по двум несовпадающим направлениям, это значит найти траекторию точки, совершающей эти колебания, в плоскости содержащей заданные направления. Задача решается аналогично нахождению траектории материальной точки брошенной под углом к горизонту (70,71).

Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях, (x = А₁cost, y = A₂ cos(t + )),

всегда есть ограниченная линия (не уходящая на бесконечность):

1. у = (А₂/А₁) x (если разность фаз  = 0) – отрезок прямой.

2. у = - (А₂/А₁) x (если разность фаз  = ) – отрезок прямой.

3. x²/A₁² + y²/A₂² = 1 (если разность фаз   /2) – канонический эллипс.

4. x²/A₁² + y²/A₂² –(2xy/ А₁ А₂)cos(₂ -₁) = sin²(₂ - ₁) – эллипс общего положения (75)

В общем случае выражения

х = А₁cos₁t и у = А₂cos(₂t +)

задают ограниченную кривую (вписанную в прямоугольник 2А₁ х 2А₂) в параметрическом виде. Причем в случае рационального отношения частот ₁ и ₂ и сдвигов фаз колебаний траектории замкнуты и называются фигурами Лиссажу. При этом отношение частот ₁/₂ равно отношению числа касаний фигуры Лиссажу с горизонтальной и вертикальной сторонами прямоугольника, в который они вписываются.

Если указанные отношения иррациональны, то траектория точки не замыкается, однако она остается внутри упомянутого прямоугольника.

Другие варианты сложения взаимно перпендикулярных колебаний различных частот представлены на рис. 18 и 19.

Направление обхода траектории всегда можно установить, рассмотрев смещение точки за малый промежуток времени t. В общем случае направление обхода можно установить, рассмотрев ориентацию вектора , построенного по правилу (векторное произведение двух векторов), где, , - радиус –вектор точки в момент времени t и ее скорость в этот же момент времени. Вектор всегда перпендику лярен плоскости x,y и если он направлен против оси z правой системы координат, то фигура обходится по часовой стрелке.

Сложение колебаний различных направлений сводится к сложению взаимно перпендикулярных колебаний.

1 2

3 4

5 6

7 8

Рис. 19. Фигуры Лиссажу

1. - x = A cos(2ωt + φ), y = B cos(ωt); 2. - x = A cos(2ωt), y = B cos(ωt + φ); 3. - x = A sin(2ωt + φ), y = B sin(ωt); 4. - x = A sin(2ωt), y = B sin(ωt + φ); 5. - x = A cos(ωt), y = B cos(2ωt + φ); 6. - x = A cos(ωt + φ), y = B cos(2ωt); 7. - x = A sin(ωt), y = B sin(2ωt + φ);

8. - x = A sin(ωt + φ), y = B sin(2ωt),(А = 1, В = 4, φ = 135⁰)