2.1.11. Затухающие колебания

Анализ затухающих колебаний, обусловленных возвращающей силой пропорциональной смещению осциллятора от положения равновесия х и силой сопротивления пропорциональной скорости движения х¹, проводим на основе уравнения

х¹¹ + 2βх¹ + ω₀²х = 0, (76)

где β – коэффициент затухания, ω₀ – собственная частота осциллятора. Его решением является затухающая гармоника (рис.20)

x = A₀e^-βtsin(ωt + ₀). (77)

Последнее решение справедливо при условии β << ω₀ .

Задача 12

Пусть проводящая рамка в виде квадрата со стороной a подвешена в магнитном поле с индукцией B на нити, коэффициент упругости которой для кручения равен k. В начальный момент времени при равновесии вектор В скользит вдоль рамки. Сопротивление рамки R, момент инерции относительно оси О равен J, ее индуктивность ничтожно мала. Будучи выведенной из положения равновесия поворотом на угол φ, рамка совершает малые колебания вокруг вертикальной оси симметрии, проходящей через ее центр масс. Написать уравнение колебаний.

Решение.

При повороте рамки магнитный поток, пронизывающий ее, возрос до величины

Ф = ВS sin φ.

При этом в рамке возникает ЭДС Ɛ_и индукции и индукционный ток:

Ɛ_и = - = - BS cos φ  ; I = Ɛ_и /R.

Возникший индукционный ток порождает магнитный поток, направленный через контур рамки против . Сила F, действующая на каждую из вертикальных сторон рамки, равна

F = I a B sin α (α = 90⁰) .

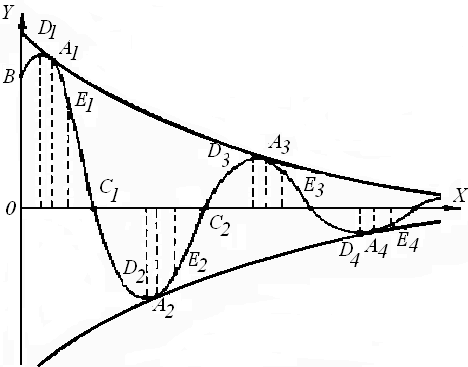
Рис.20. Функция y = A e ^–X sin (x + ₀) – график затухающего колебания

Точки пересечения с осями: В (0, Аsin φ₀), С₁, С₂, С₃ . . .((kπ – φ₀) /ω, 0). Точки касания асимптот с графиком: А₁ , А₂, А₃, …: (((k + ½) - ₀)/: (- 1)^k A e^-X). Экстремумы: D₁, D₂, D₃, …. при (k - ₀ - )/. Точки перегиба: Е₁, Е₂, Е₃, … при (k - ₀ + 2)/, где tg α = ω/

На горизонтальные стороны рамки силы не действуют.

Силы магнитного взаимодействия создают вращающий момент направленный против возрастания угла φ: М = 2 F h. Здесь h – плечо силы F. Из рис. h = (a/2) cos φ. Как видно из рисунка, этот момент возвращающий.

Направление индукционного тока определяем по правилу Ленца, а направление силы магнитного взаимодействия по правилу левой руки.

Кроме того, силы упругости, возникающие при закручивании нити на малый угол, создают свой возвращающий момент сил

М₁ = - k φ (k = , J_р = 0,5 πR⁴ , G = 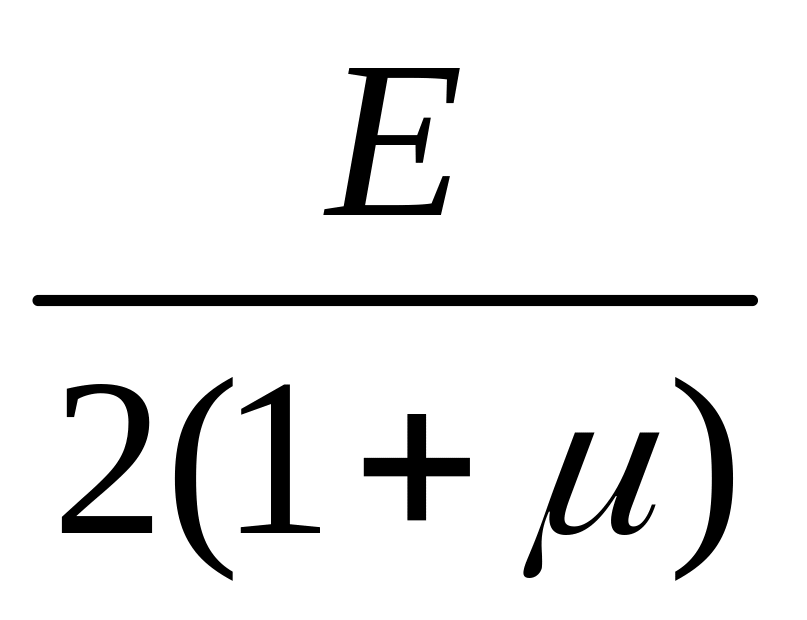, J_р – момент инерции сечения подвеса в виде проволоки радиуса R, Е – модуль Юнга и μ – коэффициент Пуассона материала проволоки).

В приближении малых углов поворота имеем

Ф = В а², Ɛ_и = -- B а² , I = - .

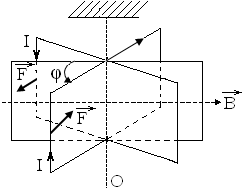
Рис. 21. Рамка, колеблющаяся в магнитном поле

Уравнение моментов для движения рамки представляется в виде

J φ¹¹ + φ¹ + αφ = 0.

Оно легко приводится к стандартному виду при

2β = , ω₀ ² = .

Разумеется, колебания возникнут при ω₀  β.

Крутильные колебания

Крутильные колебания достаточно часто встречаются в природе и технике. Здесь мы продемонстрируем, как производится учет сил трения, приводящих к затуханию таких колебаний.

Произведем учет сил вязкости при крутильных колебаниях, которые обусловливаются затуханием колебаний. Сила вязкости, действующая на тело при его движении в газе, определяется по формуле: F_в = η. grad v .dS , grad v = dV/dX- градиент скорости при движении твердого тела в жидкости или газе, dS - площадь соприкосновения твердого тела с потоком газа, η – коэффициент вязкости. Условия обтекания твердых тел газами таковы, что на поверхности тел частицы жидкости имеют ту же линейную скорость, что и тела (эффект прилипания).

Решим конкретную задачу:

Диск A радиуса R, подвешенный на упругой нити между двумя неподвижными плоскостями, совершает крутильные колебания вокруг своей оси OO’. Момент инерции диска относительно этой оси J, зазор между диском и каждой из плоскостей h, причем h << R. Найти вязкость газа, окружающего диск A, если период колебания диска T, а логарифмический декремент затухания λ.

Выделим на диске кольцо площадью dS на расстоянии r от центра. Площадь этого кольца определяется по формуле

dS = π(r+dr)² - πr² = 2πrdr, (78)

в пренебрежении бесконечно малыми 2-го порядка, содержащими dr. Линейная скорость точек этого кольца

v = ω.r ,

где ω - угловая скорость вращения диска радиуса R. Градиент скорости на одной из сторон диска составит

grad v = dv/dх = v/h = ωr/h , (79)

т.к. при движении твердых тел в жидкости или газе имеет место «эффект прилипания», состоящий в том, что скорость жидкости на поверхности тела равна нулю.

Элемент силы вязкости действующий на рассматриваемое кольцо равен

dF = η. grad v .dS = η.( ωr/h) 2πrdr.

Элемент момента сил dF действующий на кольцо

dN_в = dF.r = (2π ωr/ h) r² dr .

Для того, чтобы найти полный момент сил вязкости действующий на диск, надо проинтегрировать по радиусу r.

.

Это полный момент сил вязкости действующих на одну плоскость. Как видно, момент сил трения (вязкости) пропорционален угловой скорости колебаний. Обратимся к уравнению движения твердого тела в виде вращения вокруг неподвижной оси под действием момента сил трения (вязкости) и момента упругих сил kφ.

Jε =- N_b- N_учр= -bω - kφ ,

где b = (πωηR⁴)/2h

Приведем уравнение колебаний к стандартному виду:

φ^″ + 2βφ^′ + ω²₀φ = 0,

2β = b/J ; ω²₀ = k/J,

J – момент инерции колеблющегося диска. По условиям задачи с учетом 2-х поверхностей, между которыми колеблется диск. Имеем

.

Энергетические соотношения Полная механическая энергия системы состоит из кинетической энергии колеблющейся материальной точки Е_К и потенциальной энергии деформированной пружины Е_П.

Е = Е_К + Е_П = 0,5 (kx² + mv²).

Пусть x = A₀e^-βtcos(ωt + ₀).

Введем обозначения (см. с. 171): sin α = ω /ω₀, cos α = β /ω₀, ω₀² = k/m, ω ² = ω₀² + β².

Тогда v(t) = - A₀ω₀ e^-βtcos(ωt + ₀ - α).

E (t) = 0,5 ( k A₀² e^-2βtcos²(ωt + ₀) + m A₀² ω₀²e^-2βt cos²(ωt +

₀ - α)) = 0.5k A₀² e^-2βt(0.5(1 + cos2(ωt + ₀ )+1+ cos2(ωt +

₀ - α))= 0.5k A₀² e^-2βt(1+cos((2 ωt+2₀+2 ωt+2j₀-2

α)/2)cos((2 ωt+2₀ -2 ωt-2j₀ +2 α)/2)= 0.5k A₀² e^-2βt(1+cosα

cos(2ωt+2j₀ -α))= 0.5k A₀² e^-2βt(1+( β/ω₀)cos(2ωt+2j₀ -α))

(80)

Зависимость E (t) представляет собой сумму экспоненты и затухающей гармоники.

Затухающие колебания в электрических цепях

Колебания в электрических цепях содержащих активное сопротивление (резистор) R, электроемкость С и индуктивность L также являются затухающими. Для вывода базового уравнения рассмотрим закон сохранения энергии. Работа источника тока (генератора) по перемещению электрических зарядов в цепи за время dt равна IƐ dt, где I - сила тока в цепи, Ɛ - напряжение на генераторе.

Эта работа переходит в тепло dQ выделяемое на резисторе и идет на изменение энергии электромагнитного поля dW. Количество выделившейся теплоты dQ = I²Rdt.

Электромагнитная энергия состоит из энергии накопленной в конденсаторе W_с = q²/2C и в индуктивности W_L = LI²/2. Поэтому имеем:

IƐ dt = I²Rdt + dW, (81)

W = , .

Учитывая, что I = , имеем

Ɛ , (82)

что легко приводится к стандартному виду, если принять следующие обозначения:

2β = , ω₀² = , f = .