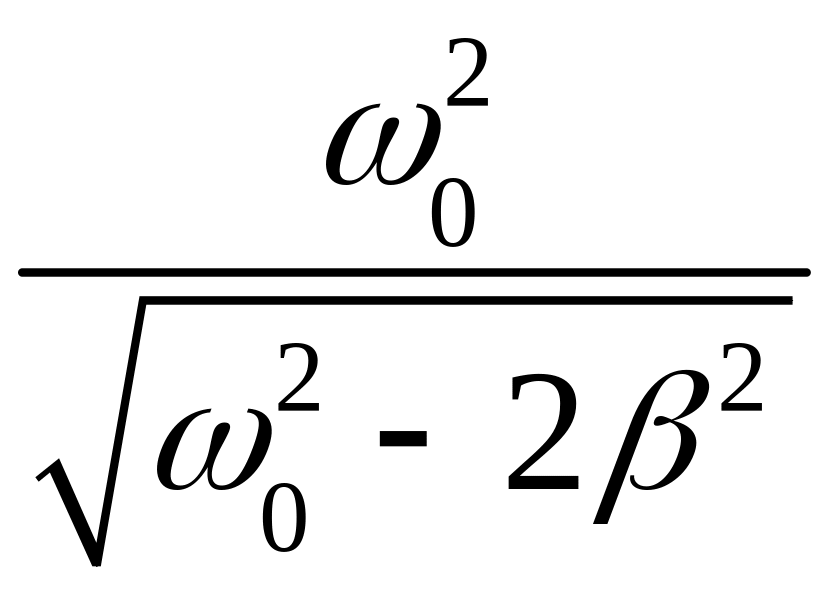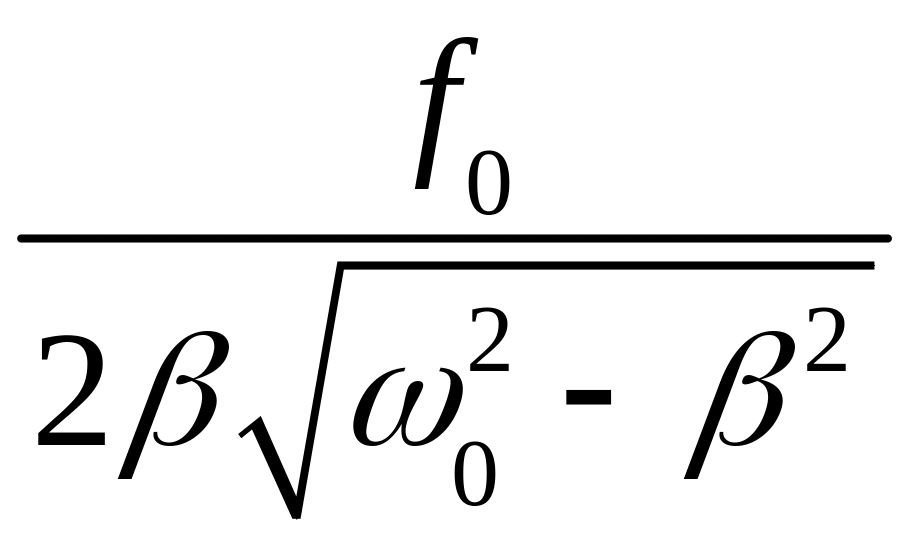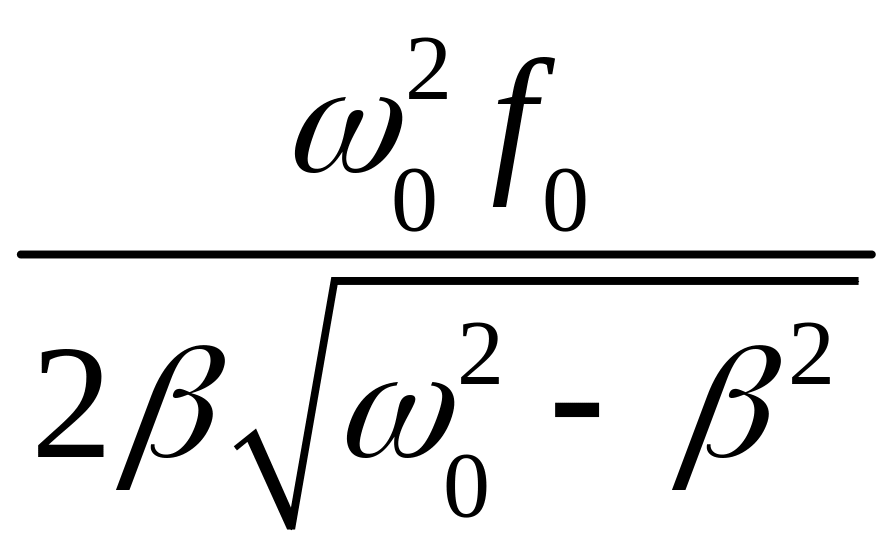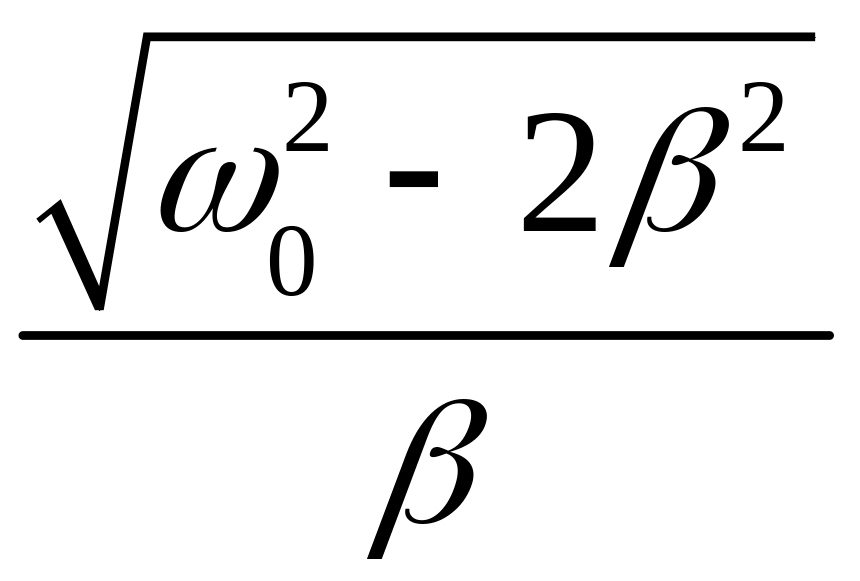2.1.12. Релаксационные колебания

Если затухание в системе велико β² > ω₀² , то имеют место решения уравнения (76) в виде релаксационных (апериодических) движений (колебаний) (рис. 21).

x = C₁exp(-β - )t + C₂ exp(-β + )t ;

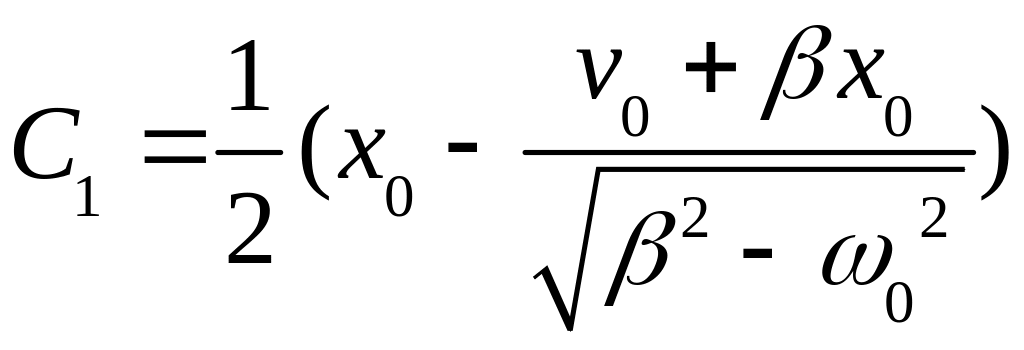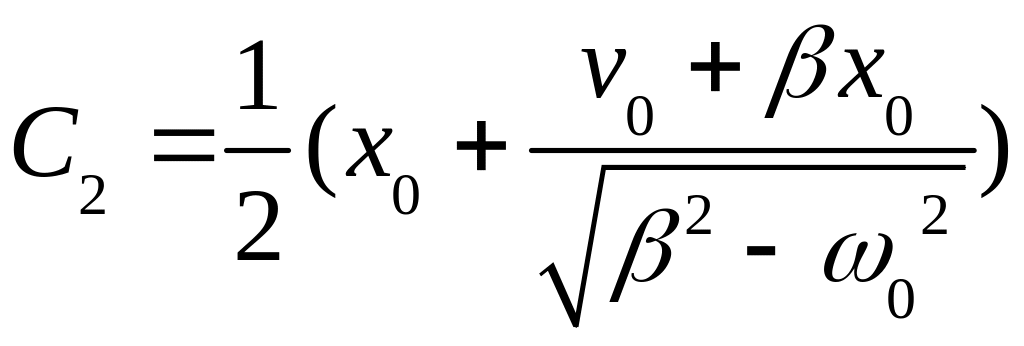; . (83)

Если β² = ω₀², то решения исходного уравнения представимы в виде

x(t) = e^-βt(x₀ + (₀ + βx₀)t). (84)

Это также релаксационные процессы. Здесь х₀ и v₀ – начальные смещение и скорость осциллятора. Показать, что решения (77) и (83) удовлетворяют дифференциальному уравнению (76) при указанных условиях, можно методом подстановки.

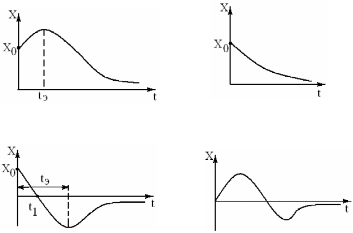
Рис. 21. Различные виды релаксационных движений (х₀ – начальное смещение, t₁ – момент времен, когда материальная точка проходит положение равновесия, t_э – момент времени, когда достигается максимальное отклонение от положения равновесия)

2.1.13. Вынужденные колебания. Резонанс смещений, скоростей и ускорений

Анализ вынужденных колебаний проводим на основе уравнения (62) для смещения, приведя его к стандартному виду

х¹¹ + 2βх¹ + ω₀²х = f (t), (85)

где f (t) – вынуждающая сила, действующая на единичную массу. Если f (t) = f₀ cosωt, то решение в виде установившихся колебаний задается соотношением (63):

x = a cos(ωt - ),

где

a = f₀/( ) (86)

– амплитуда колебаний, сдвиг фаз между установившимися колебаниями и вынуждающей силой задается соотношением

tg  = 2βω/(ω₀² – ω²). (87)

Для амплитуд скоростей и ускорений соответственно имеем:

V(ω) = ωf₀/( ),

A (ω) = ω² f₀/( ). (88)

Важной характерной чертой вынужденных колебаний, кроме переходного процесса (рис. 22), является наличие резонанса смещений, скоростей и ускорений, в зависимости от того, частотная характеристика амплитуды и фазы какой из этих величин рассматривается.

Приведем важнейшие результаты изучения резонансных кривых А(ω), V(ω), A(ω) в таблице 2.

Таблица 2

	Резонанс смещений А(ω)	Резонанс скоростей V(ω) = ω А(ω)	Резонанс ускорений A(ω) = ω2 А(ω)
Резонансная частота	ωрА =	ωрV = ω0	=
Амплитуда в резонансе	А(ωрА) =	V(ωрV) =	A ( ) =
Поведение на низких частотах	А(0) =	V(0) = 0	A ( ) = 0
Поведение на высоких частотах	А( ) = 0	V( ) = 0	A ( ) =
Сдвиг фаз на резонансной частоте	tg φ(ωрА) = -	φ(ωрV) =	tg φ( ) = =
Примечания	β < ω0

Универсальный вид резонансных кривых

Будем исходить из выражения для амплитуды скорости при резонансе

V(ω) = ωf₀/( ).

Учтем, что на резонансной частоте амплитуда скорости равна V(ω_р) = f₀/2β. Введем относительную амплитуду скорости

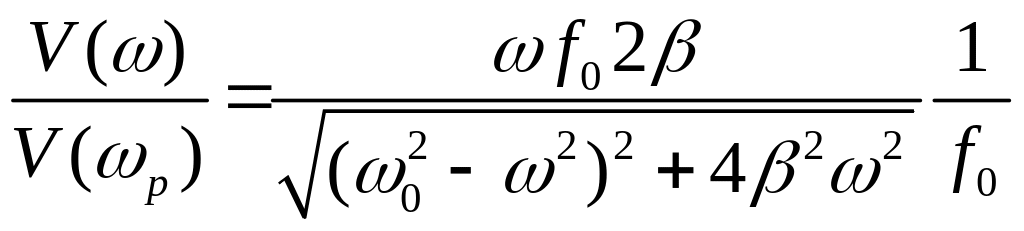
Введем добротность Q по формуле Q = . Тогда

=

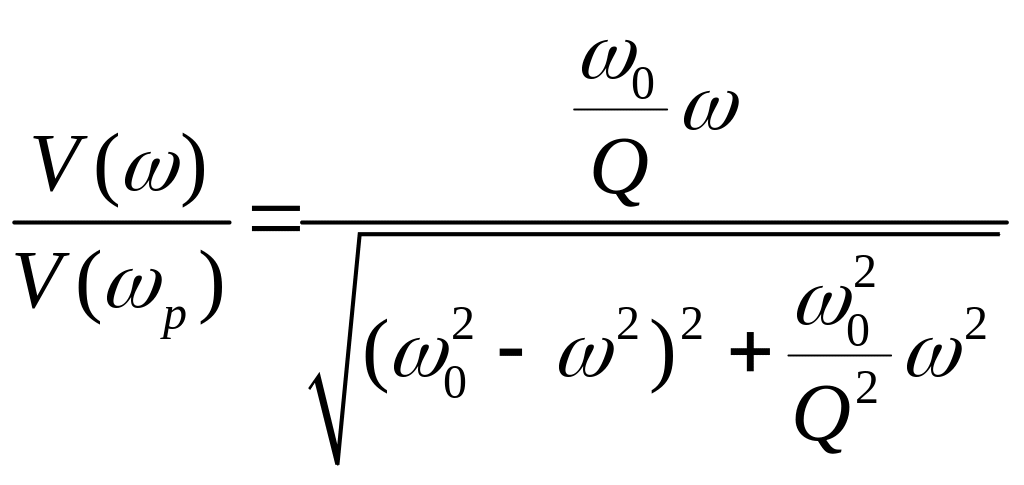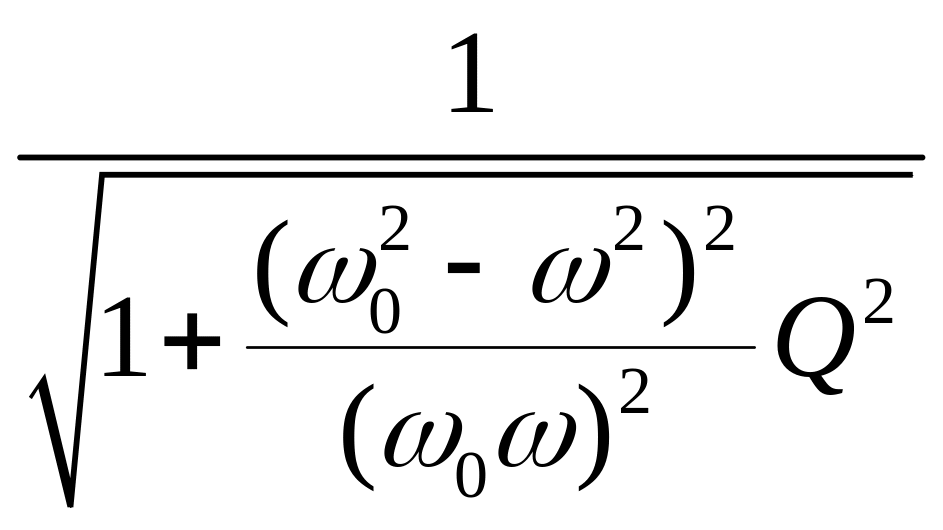
Преобразуем выражение

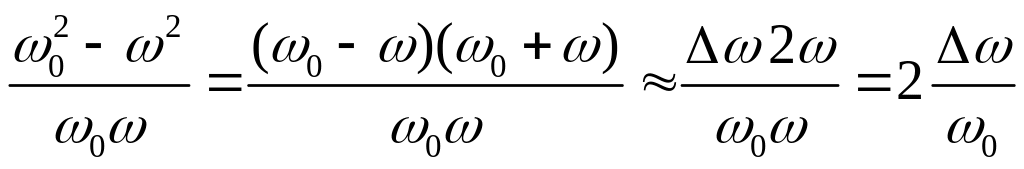
Полученную величину назовем относительной расстройкой резонансного контура.

Окончательно имеем

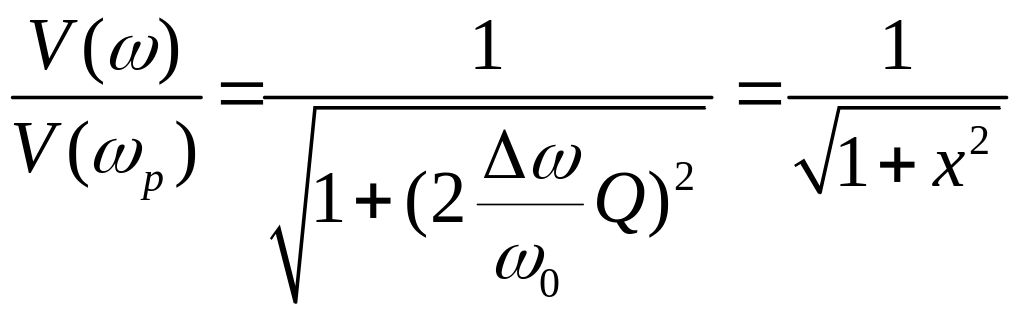. (89)

Эта элементарная функция хорошо изучена и составлены соответствующие математические таблицы.

Аналогичным образом можно представить и другие резонансные кривые.

Итак, для того, чтобы колебания системы приобрели резонансный характер необходимо:

- чтобы система могла колебаться с частотой (вынуждающей) внешней силы;

- чтобы затухание в системе было мало (β < ω₀) ;

- чтобы частота внешней силы была близка к частоте собственных колебаний системы;

- чтобы переходной процесс закончился (τ > 1/β).

В целом ряде случаев целесообразно избегать резонанса, т.е. погасить колебания.

Для этого необходимо:

- чтобы колебательная система имела собственные частоты далёкие от частоты внешних воздействий и от частот, кратных частоте внешних периодических (но не гармонических) воздействий (см. теорему Фурье);

- в системе должно быть значительное затухание (β > ω₀) ;

- применять демпфирование колебаний.

Рассмотрим последний случай детальнее на простом примере. Пусть имеется материальная точка массой М, подвешенная на пружине жесткостью К. Пусть к этой материальной точке прикреплена пружина жесткости k и к этой пружине материальная точка массой m. Пусть на точку М действует внешняя гармоническая сила

F₀ sinωt. Поскольку постоянная сила тяжести только смещает положение устойчивого равновесия, не будем ее учитывать. Уравнение движения массы М имеет вид

MX^" = - KX – k(X - x) + F₀ sinωt ,

а массы m -

mx^" = k(X - x).

Здесь k(X - x) – сила, с которой взаимодействует эти массы посредством пружины жесткостью k; Х – смещение массы М от положения равновесия, а х – смещение другой массы от своего положения

равновесия. Так как имеет место установившийся колебательный режим, то решения этих уравнений можно искать в виде

X = A sinωt; x = a sinωt.

Вторые производные этих смещений

X^" = -ω² A sinωt и x^" = -ω² a sinωt.

Подставим это выражение в первое и второе уравнения движения масс соответственно. Получим:

- M ω² A + KA + k(A - a) - F₀ = 0,

- mω²a - k(A - a) = 0.

Из второго выражения сразу имеем:

A = a.

Это выражение обращается в нуль, как только ω = ω₀ = . Из первого выражения при А = 0 имеем а = - F₀/k. Таким образом, при А = 0, т.е. при Х = 0 сила, действующая со стороны второго тела на первое имеет вид:

f₁₂ = - k(X - x) = kx = - F₀ sinωt = F₀ sin(ωt + π) ,

т.е. она равна по величине и противоположна внешней вынуждающей силе. Поэтому первое тело вообще не колеблется. Имеет место демпфирование колебаний.