§5. Производная по направлению. Градиент.

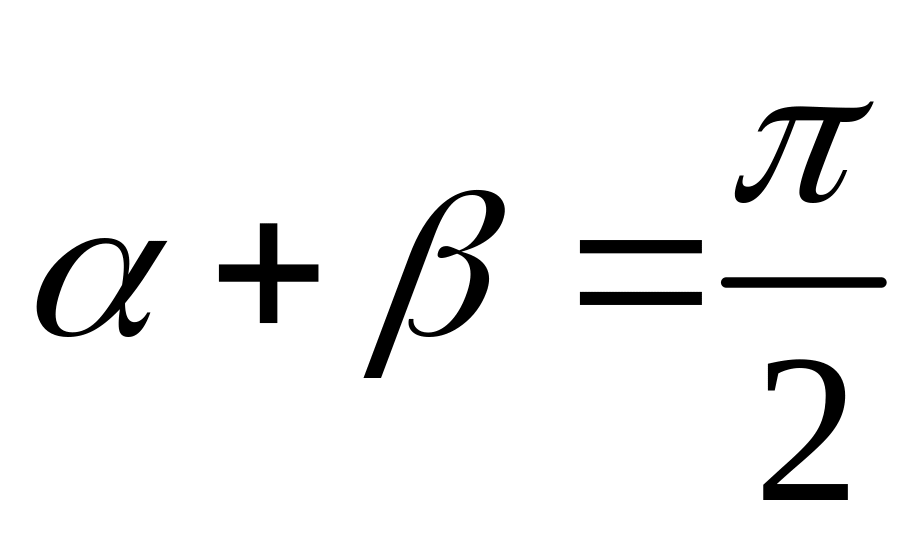а ) Пусть функция определена в некоторой окрестности точки , некоторое направление, задаваемое единичным вектором , где , т.к. (или ), – косинусы углов, образуемых вектором с осями координат. При перемещении в данном направлении точка в точку , функция получит приращение , называется приращением функции в данном направлении . Если , то .

Определение: Производной по направлению функции двух переменных называется предел отношения приращения функции в этом направлении к величине перемещения при стремлении последней к нулю, т.е. 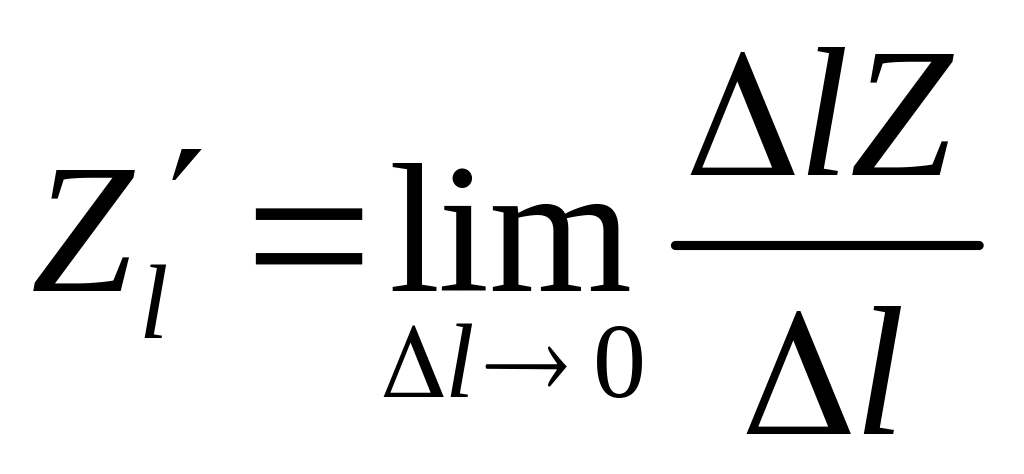( 1 )

Производная характеризует скорость изменения функции в направлении

Частные производные и представляют производные по направлениям, параллельным осям ОХ и ОУ.

( 2 ) или

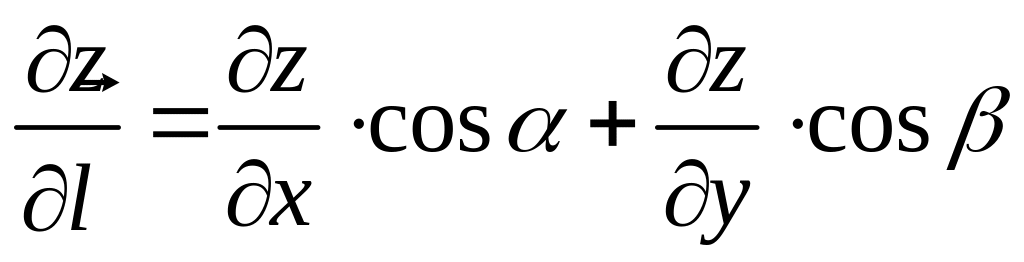
Абсолютная величина производной определяет величину скорости, знак производной – характеризует изменения функции .

Если знак – возрастает

Если знак – убывает.

б) Градиентом функции называется вектор с координатами .

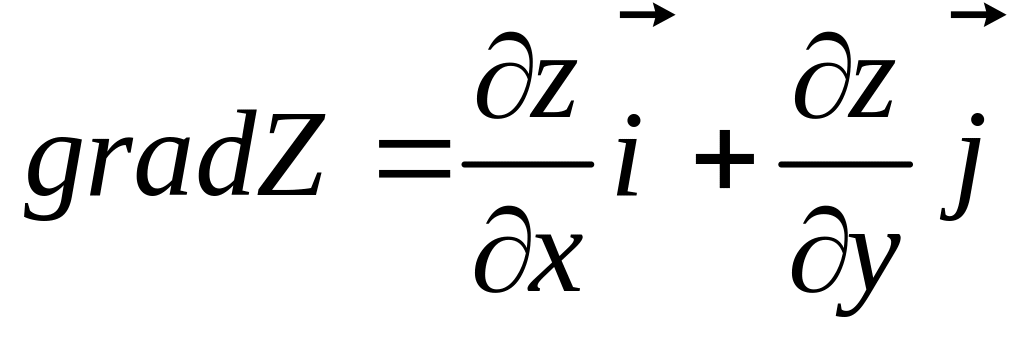
Рассмотрим скалярное произведение векторов и

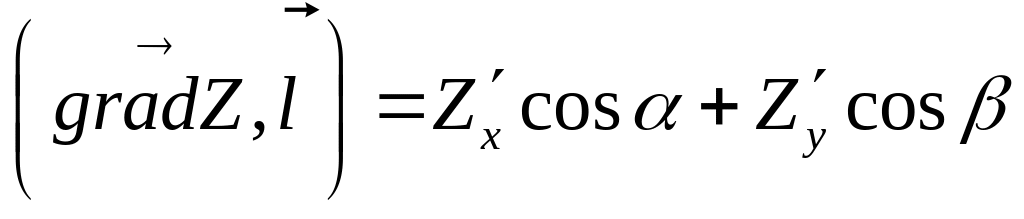( 3 )

Сравниваем (2) и (3) получаем что 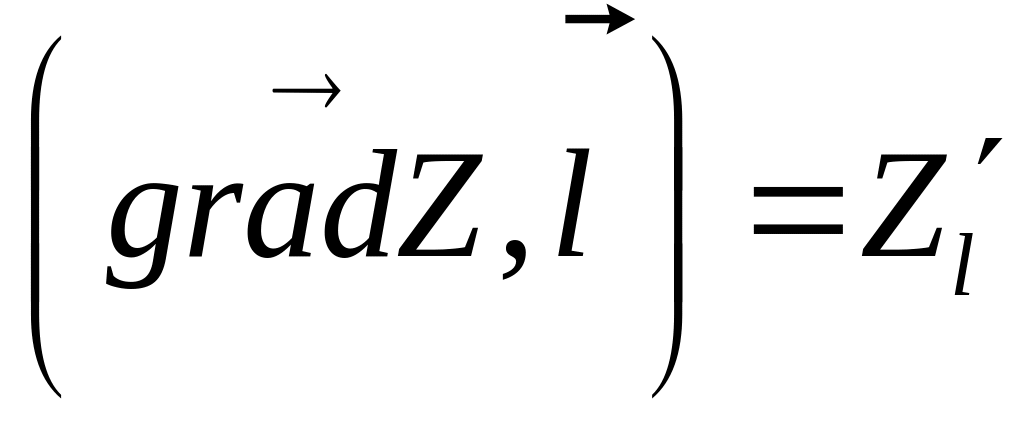, т.е. производная по направлению есть скалярное произведение градиента и единичного вектора задающего направление .

С калярное произведение двух векторов максимально, если они одинаково направлены, следовательно, градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Зная градиент функции в каждой точке, можно строить линии уровня функции.

Теорема. Пусть задана дифференцируемая функция и пусть в точке величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку. Чтобы построить линии уровня поступают так: строим градиент в точке , задаем направление перпендикулярное градиенту. Оно позволяет построить малую часть линии уровня. Далее рассмотрим близкую точку и строим градиент в ней. Продолжая этот процесс можно (с определенной погрешностью) построить линии уровня.

Пример. Найти производную и градиент функции в точке по направлению вектора .

Решение:

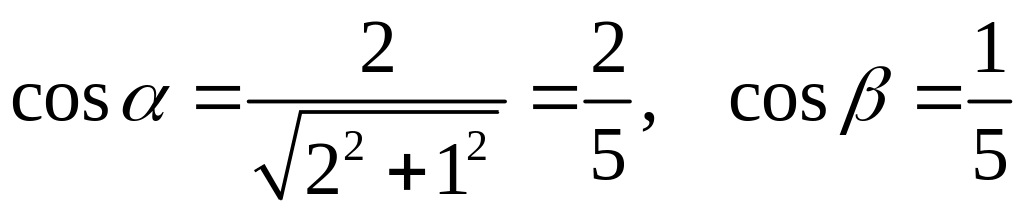
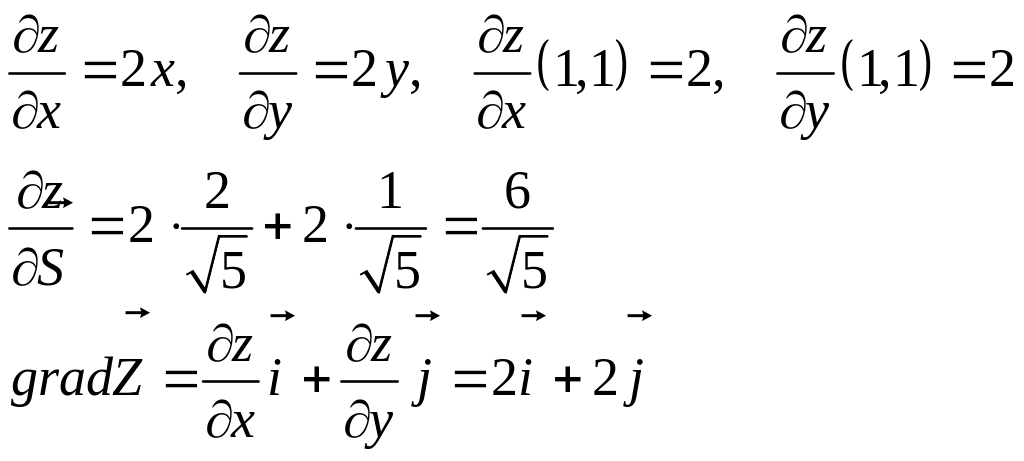
Лекция 29.

§6. Экстремум функции нескольких переменных.

Точка называется точкой максимума (минимума) функции , если существует окрестность точки такая, что для всех точек из этой окрестности выполняется неравенство

Необходимое условие экстремума:

Т еорема: Пусть точка – есть точка экстремума дифференцируемой функции . Тогда частные производные и в этой точке равны нулю. Точки, в которых называются критическими или стационарными.

Замечание 1: В точках максимума или минимума дифференцируемой функции градиент равен нулю.

Замечание 2: В точках экстремума обращаются в нуль производные функции по всем направлениям.

Частные производные второго порядка:

Если частные производные и сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называются частными производными второго порядка (их будет 4):

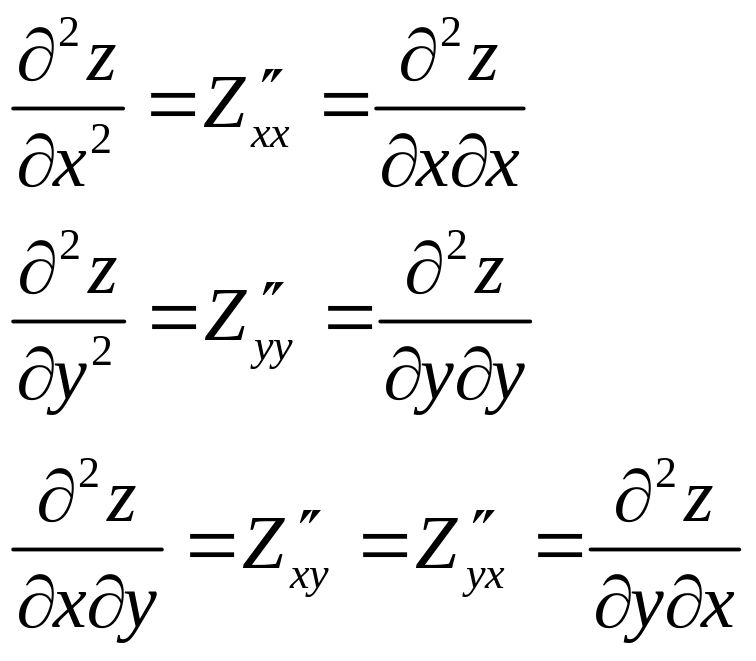
Теорема. Если частные производные второго порядка функции непрерывны в точке , то в этой точке или .

Теорема (достаточное условие экстремума функции двух переменных)

Пусть функция а) определена в некоторой окрестности критической точки , в которой и .

б) имеет в этой точке непрерывные частные производные второго порядка , тогда если

1) – то в точке функция имеет экстремум, причем если а)

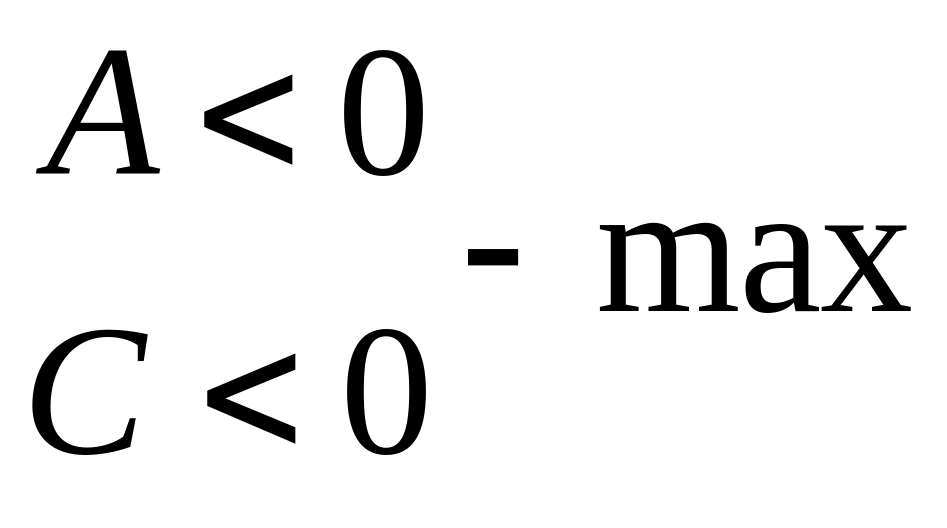
б)

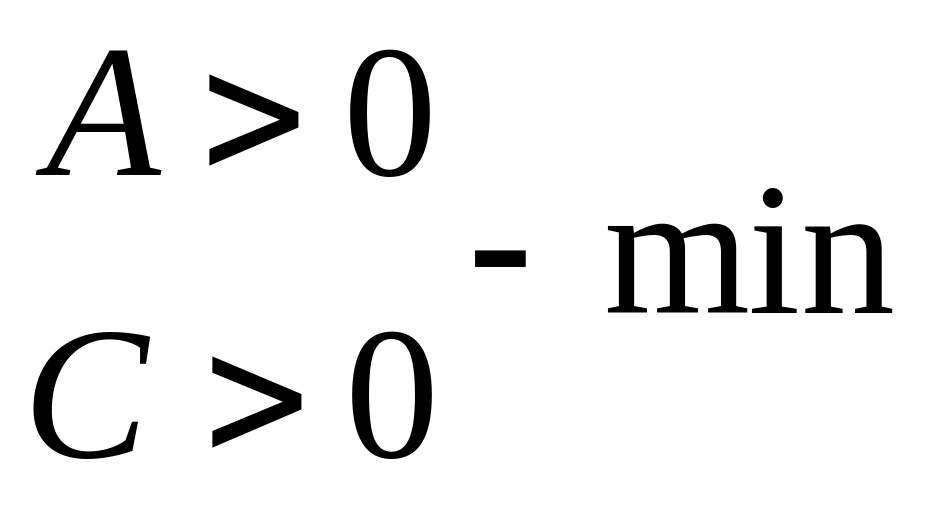
2) – функция экстремума не имеет

3) – необходимы дополнительные исследования.

Схема исследования функции двух переменных на экстремум:

1. . Найти и

2. Решить систему уравнений

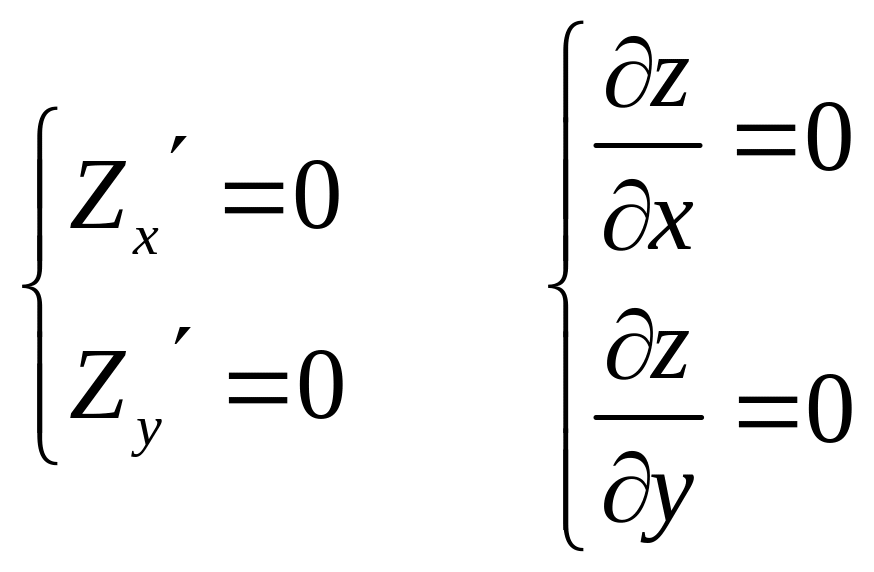
3. Найти частные производные второго порядка и с помощью достаточного признака найти и сделать вывод о наличии экстремумов.

4. Найти экстремумы функции.

Пример. Найти экстремум функции .

Решение:

1.

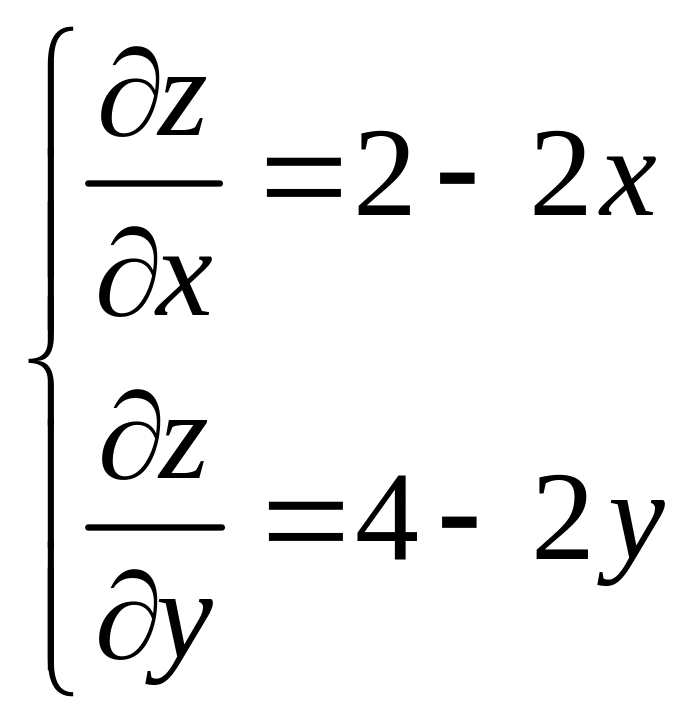
2.

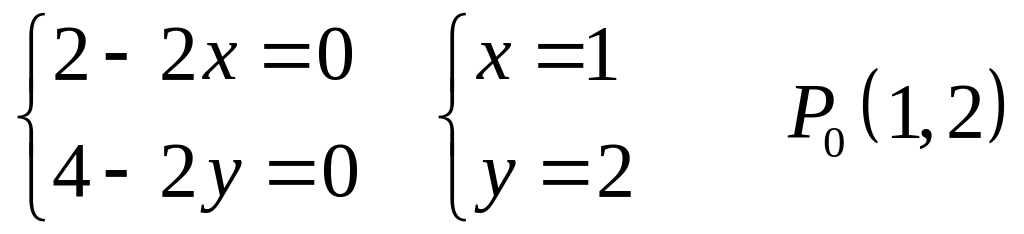
3.

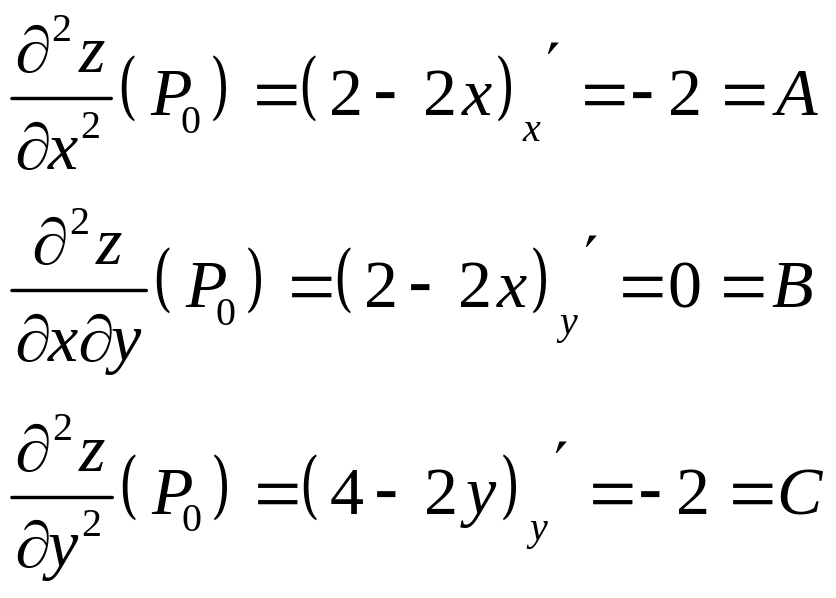
, таким образом, точка есть точка max.

4.

Лекция 30.