§2. Предел функции.

Число называется пределом функции при и (или в точке ), если для любого, даже сколь угодно малого положительного числа , найдется положительное число (зависимое от , ), такое что для всех точек , отстоящих от на расстояние меньшее, чем расстояние между точками и ), т.е. при выполняется неравенство .

Обозначается:

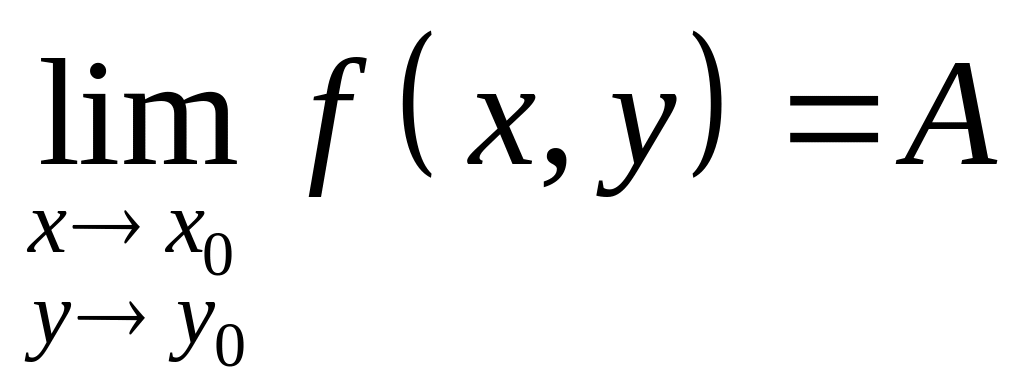
Пример. Найти предел .

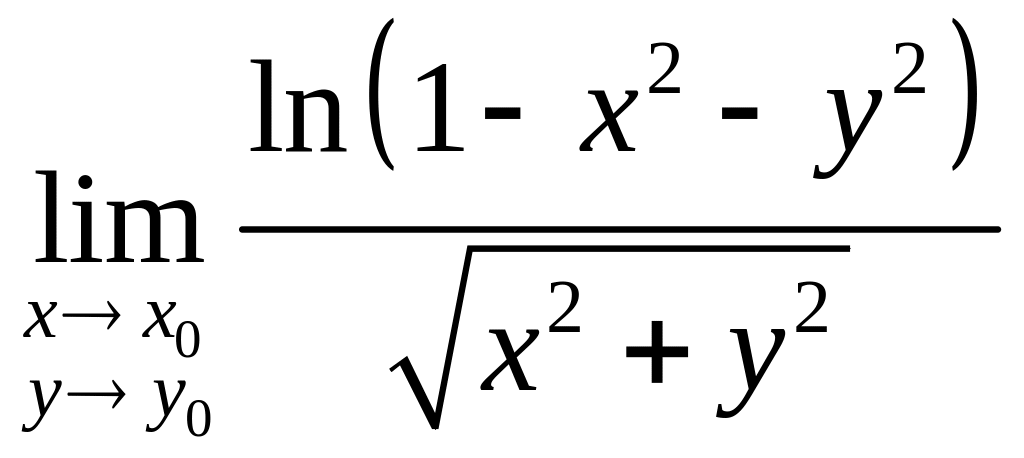Решение:

Обозначим если , то .

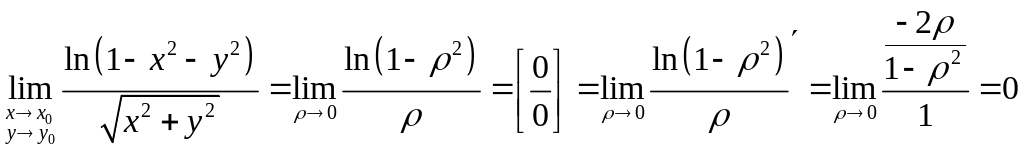
Определение: Функция называется непрерывной в точке , если она: 1) определена в точке , 2) имеет конечный предел при , 3) этот предел равен значению функции в точке , т.е. .

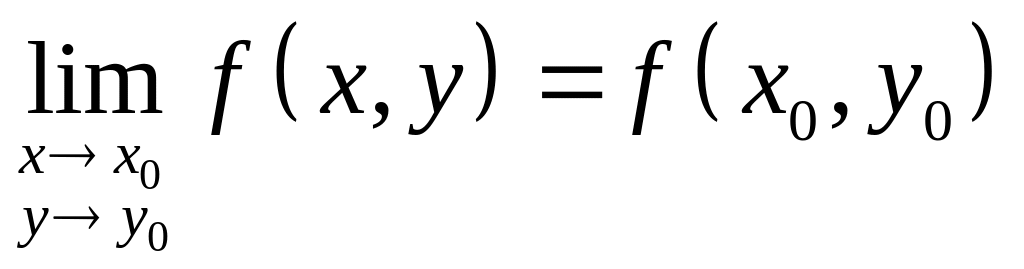геометрически: график в точке представляет собой сплошную линию, не расслаивающуюся поверхность.

§3. Частные производные.

Дадим аргументу приращение , аргументу приращение . Тогда функция получит наращенное значение . Величина называется полным приращением функции в точке . Если задать только приращение аргумента или только приращение аргумента , то получится приращение функции соответственно

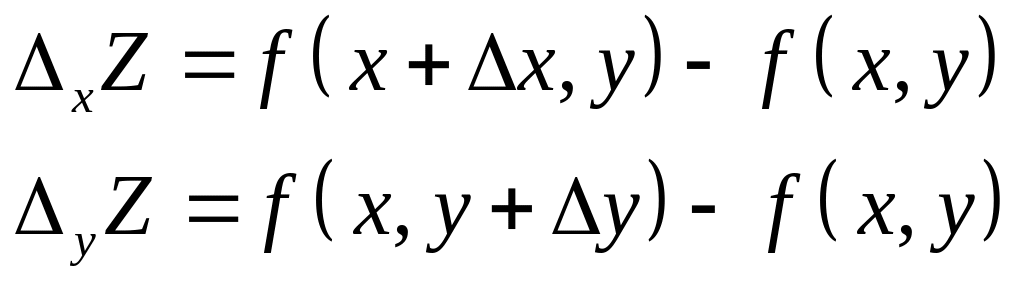
называются частными .

Пример. Найти частные и полные приращения функции .

Решение:

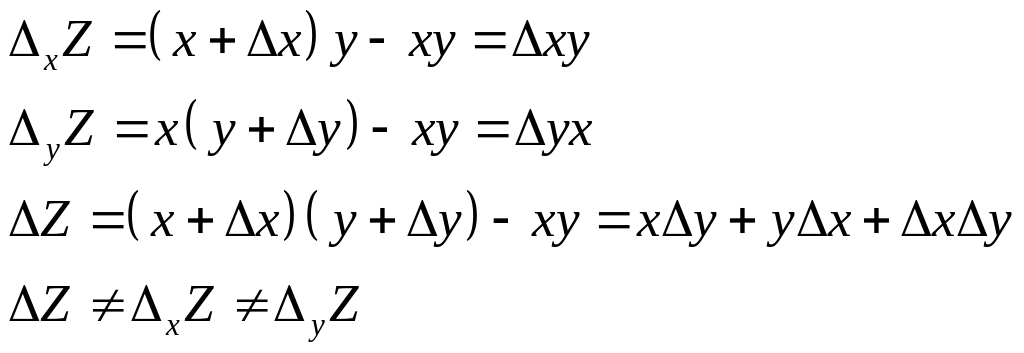
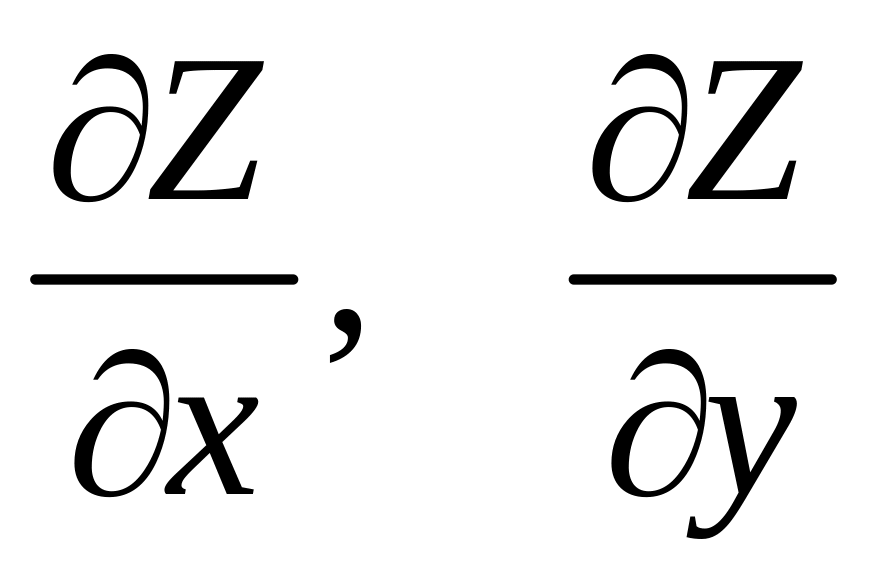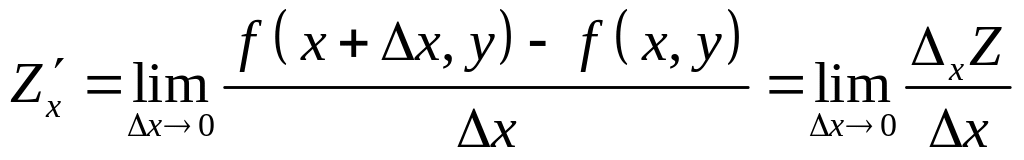Определение: Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует), обозначается или , , таким образом ( 1 )

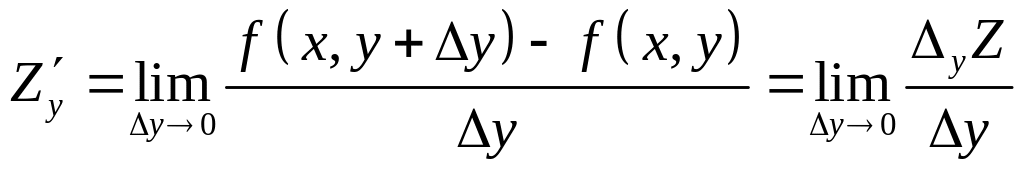( 2 )

График функции представляет некоторую поверхность . Тогда при мы получим кривую – сечение этой поверхности соответствующей плоскостью.

В этом случае выражает угловой коэффициент касательной к кривой в заданной точке , т.е. , где угол наклона касательной к оси ОХ. Аналогично, .

Правило: Для нахождения производной надо считать постоянной переменную , а для нахождения – постоянная .

Пример. Найти частные производные .

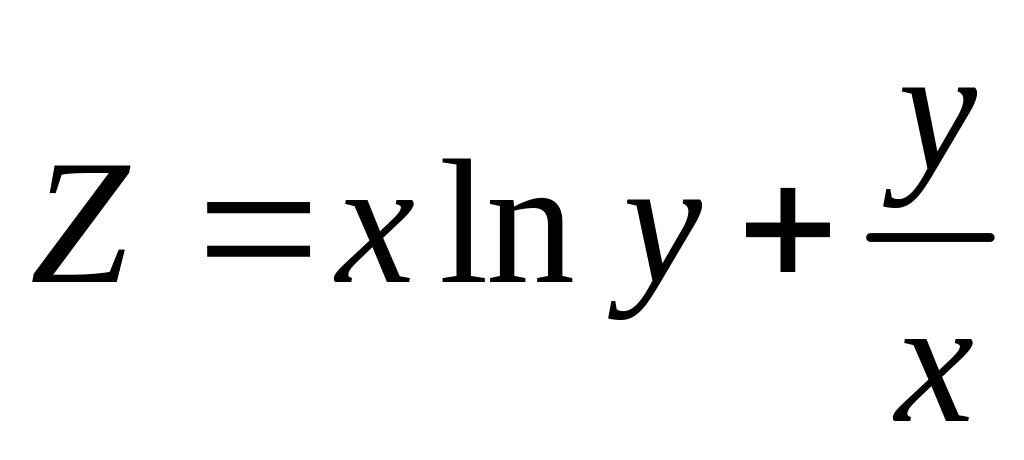Решение:

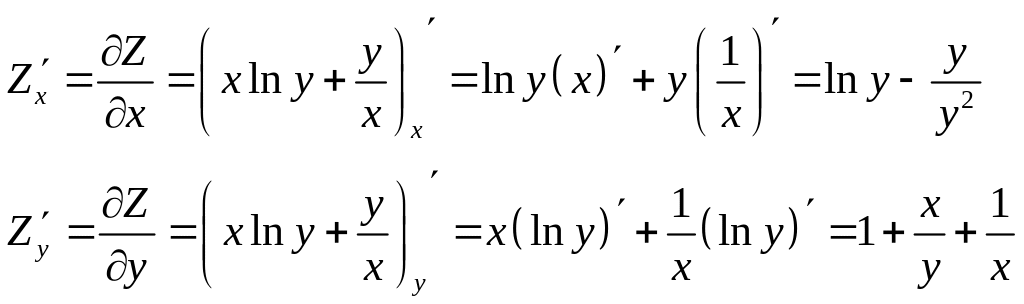
Пример. Найти частные производные .

Решение:

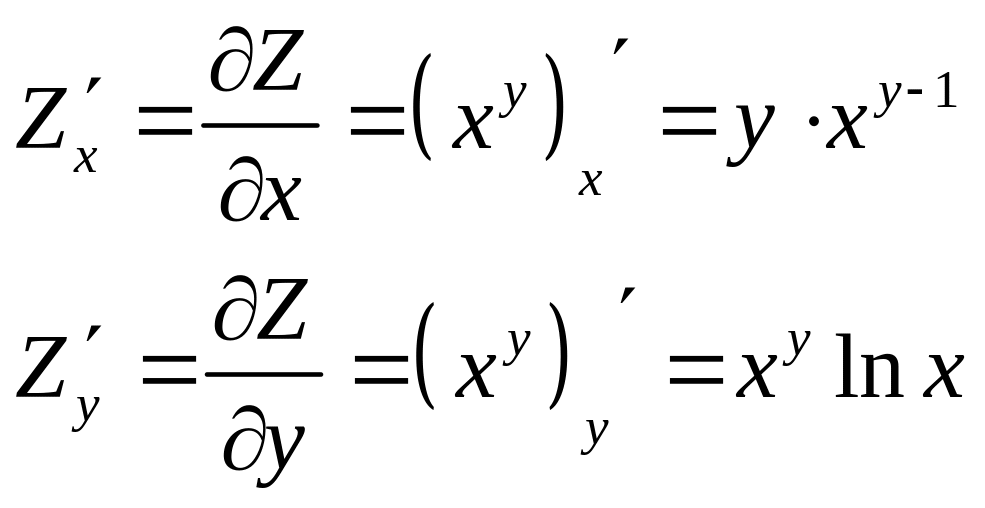
Пример. Поток пассажиров выражается функцией 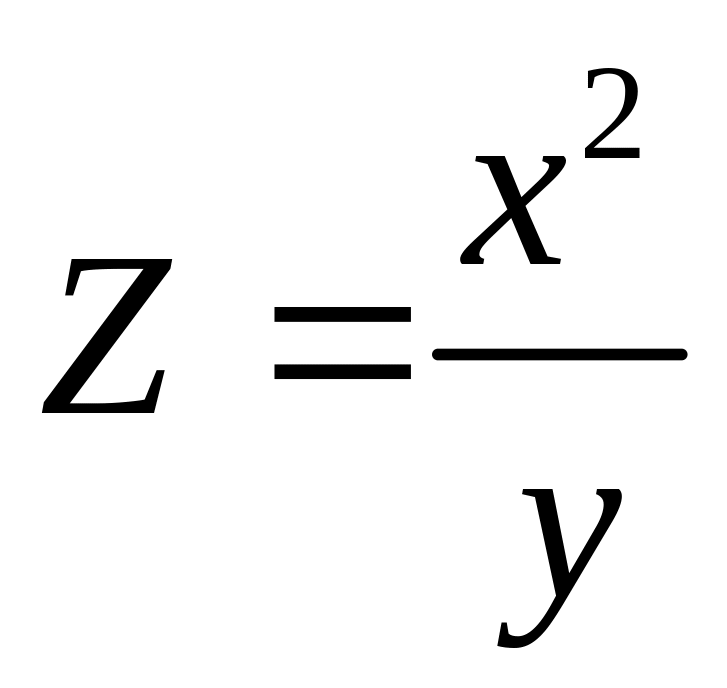, где – число жителей, – расстояние между городами. Найти частные производные и пояснить их смысл.

Решение:

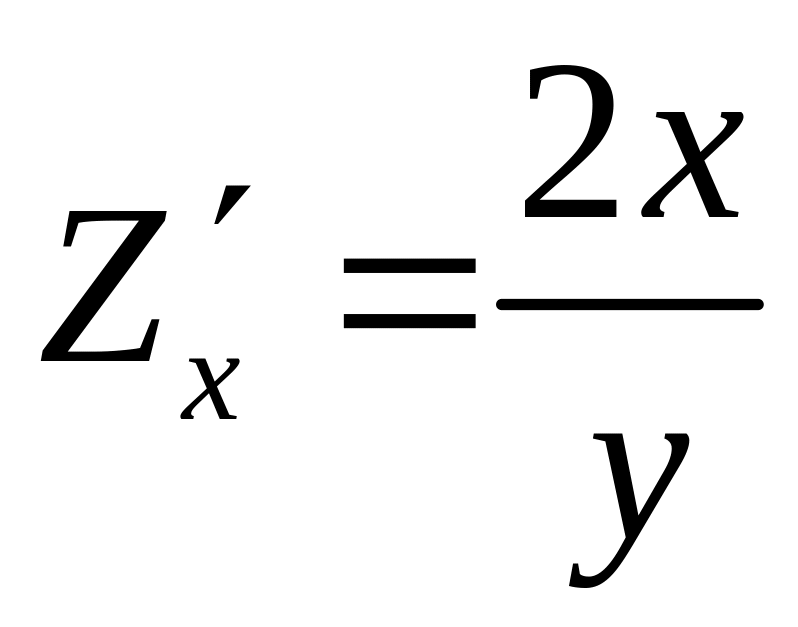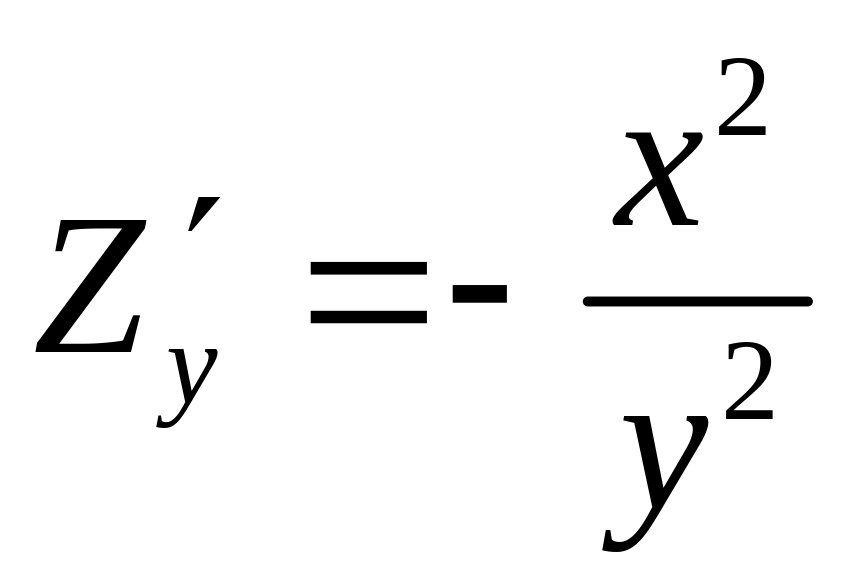Производная показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.

Лекция 28.

§4. Полный дифференциал функции.

Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных ( 1 ) , учитывая, что , , формула (1) заменяется или 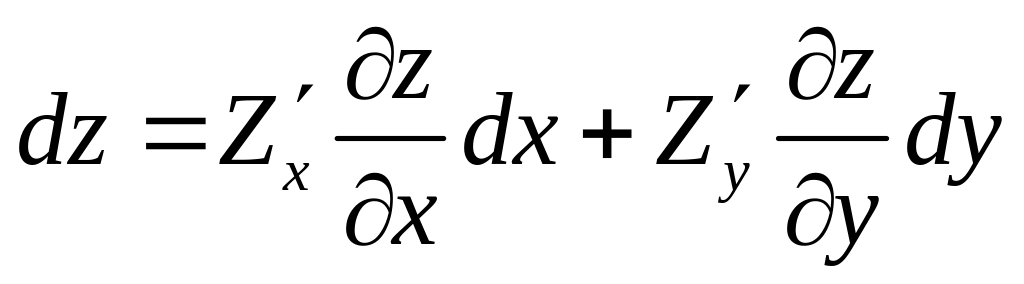( 2 ).

Функция называется дифференцируемой в точке , если её полное приращение может быть представлено в виде

( 3 )

– дифференциал функции, – б/м при .

геометрически:

Полное приращение функции равно приращению аппликаты графика функции при переходе из точки в точку . – есть приращение аппликаты касательной плоскости к поверхности в данной точке, когда переменные и получат приращение и .

Теорема. Если частые производные функции существуют в окрестности точки и непрерывны в самой точке , то функция дифференцируема в этой точке (существование частных производных является лишь необходимым, но недостаточным условием дифференцируемости функции).