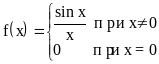1.4.3.15. Сложная функция и ее непрерывность

Пусть функция x=(t) задана на множестве {t}, и пусть {x}- множество ее значений. Допустим, что на множестве {x} задана функция y=f(x). Тогда на множестве {t} задана сложная функция y=f((t))=F(t). Предположим, что a(t) является предельной точкой множества {t}; a(t); b=(a)  {x} является предельной точкой множества {x}.

Теорема. Пусть x=(t)  C{a}, y=f(x)  C{b}, где b=(a). Тогда y=f((t))=F(t)  C{a}.

1.4.3.16. Замечательные пределы Первый замечательный предел

Доказательство. Сначала установим справедливость неравенства 0<sinx<x<tgx при 0<x< . (1)

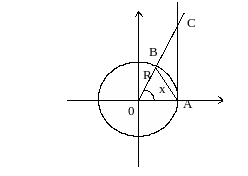
Рассмотрим следующие фигуры (см. рис. 1):

треугольники AOB и АОС и сектор АОВ Для них SAOB<Sсект. АОВ<SАОС, т.е. . Сокращая на , получаем неравенства (1) Пусть 0<x< .

рис.10

Из (1) деля на sinx, имеем 0<1< или cosx< .

Эти неравенства справедливы и для значений x, удовлетворяющих условиям , так как cosx=cos(-x) и . Функция y=cosx - непрерывна на всей числовой оси (см., например, Ильин В.А., Позняк Э.Г. Основы математического анализа.- М.: Наука, 1971, ч.1, гл.4, ?5, п.6, с.120) поэтому . Итак, для функции cosx, 1, в некоторой -окрестности точки x=0 выполняются все условия теоремы 2 п.3.12. о предельном переходе в функциональных неравенствах(f(x)=cosx, g(x)=1, h(x)= и = ).

Следовательно, .

Второй замечательный предел

Число е было определено как

Можно доказать, что е= .

1.4.3.17. Точки разрыва функций

Устранимый разрыв.

Определение 1. Точка а называется точкой устранимого разрыва функции y=f(x), если существует , но в т. а f(x) либо не определена, либо f(а) .

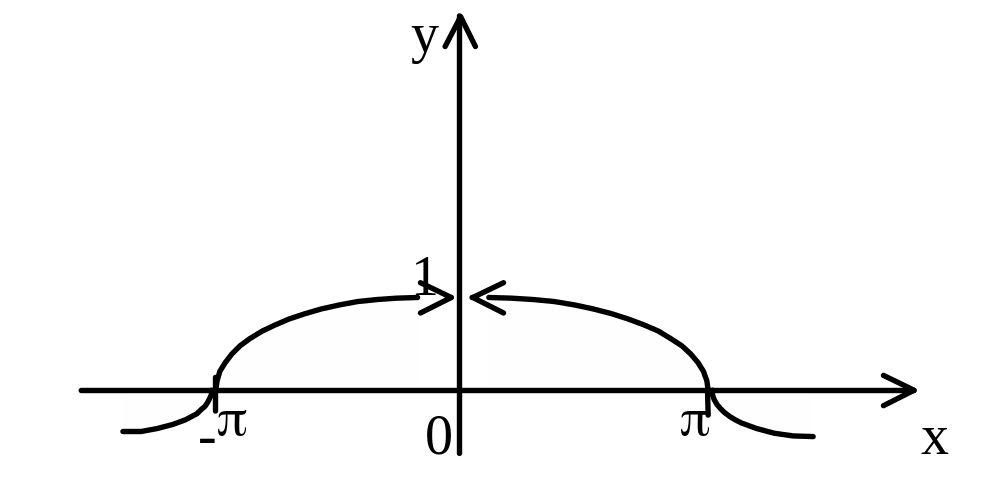
Пример 1.

Рис.11

Так как , то т. x=0 является для этой функции точкой устранимого разрыва.

Замечание 1. В точке а устранимого разрыва функции f(x) можно переопределить (или доопределить) так, чтобы она стала непрерывной, положив ее равной в т. а значению предела f(x) при xа. В примере 1 достаточно положить f(0)=1 и f(x) станет непрерывной в т. x=0 (и на всей числовой прямой в силу теоремы п.1.4.3.14.).

Разрыв первого рода

Определение 2. Точка а называется точкой разрыва первого рода, если

.

Пример 2. Точка а=0 является точкой разрыва первого рода. Действительно, односторонние пределы в т. 0 существуют, но не равны между собой

Разрыв второго рода

Определение 3. Точка а называется точкой разрыва второго рода функции y=f(x), если f(x) в этой точке не имеет хотя бы одного одностороннего предела или хотя бы один из односторонних пределов бесконечен.

Пример 3. . Эта функция бесконечно большая при x, следовательно, т. а=0 - точка разрыва второго рода.

Пример 4.

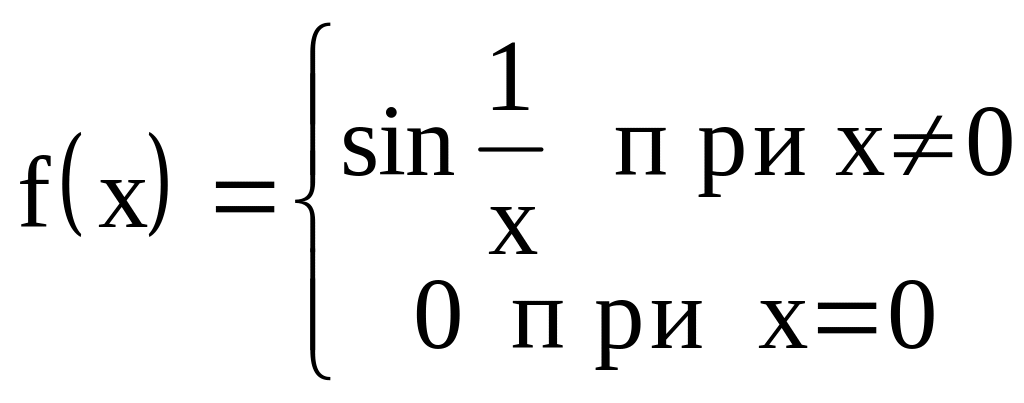
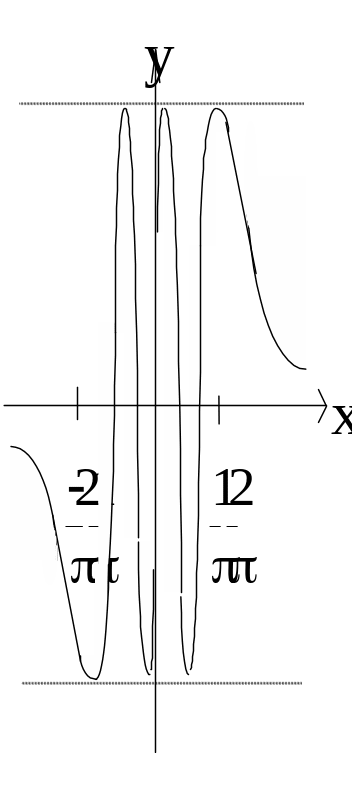
Рис. 12.

Эта функция в точке x=0, не имеет ни правого, ни левого пределов.

В силу нечетности функции достаточно проверить, что нет правого предела. Построим две положительные последовательности, сходящиеся к нулю, на которых соответствующие последовательности значений имеют разные пределы, тогда по определению Гейне функция не будет иметь правого предела в точке 0.

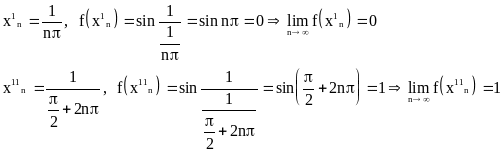
Таким образом, x=0 - точка разрыва 2-го рода.

Пример 5.

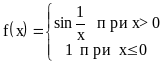
не имеет только правого предела в т. 0. Точка x=0 - точка разрыва 2-го рода.

Определение 4. Функция f(x) называется кусочно непрерывной на сегменте [a,b], если эта функция определена всюду на сегменте [a,b], непрерывна во всех внутренних точках этого сегмента, за исключением, быть может, конечного числа точек, в которых она имеет разрыв первого рода, кроме того, имеет правый предел в точке а и левый предел в точке b.