4.2 Азбука теории графов. Маршрут, путь, простой путь. Цикл. Простой цикл. Связность в графе.

Определение. Маршрутом в графе называется последовательность вершин , где пара соседних вершин является ребром графа.

-1

В этом случае будем говорить, что маршрут M соединяет вершины .

Пример.

Определение. Путем, соединяющим пару вершин будем называть маршрут, соединяющий данную пару вершин и не содержащий повторяющихся ребер.

Определение. Простым путем, соединяющим пару вершин будем называть путь, соединяющий данную пару и не содержащий повторяющихся вершин.

Определение. Пару вершин в графе будем называть связной, если либо вершины совпадают, либо существует маршрут, соединяющий две эти вершины.

Пример. Любая пара вершин в следующем графе связана:

В следующем графе связанными являются не все вершины:

Вершины 1 и 2 связаны, а, например, вершины 2 и 3 не связаны.

Утверждение. Если в графе существует маршрут, соединяющий пару вершин, то существует простой путь, который соединяет данную пару вершин.

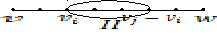
Рассмотрим маршрут, соединяющий вершины . Предположим, что вершина повторяется на маршруте. Тогда вырежем участок маршрута между повторяющимися вершинами и соединим полученные части. Данную операцию будем повторять до тех пор, пока в маршруте не будет повторяющихся вершин.

Таким образом, получен простой путь, соединяющий пару вершин . Поэтому для связности вершин достаточно наличие простого пути, который их соединяет.

Определение. Циклом называется путь, в котором начальная и конечная врешины совпадают.

Пример.

Определение. Простым циклом называется путь, в котором вершины не повторяются, за исключением первой и последней. Другими словами, простой цикл - это цикл без самопересечения.

Пример. Простой цикл:.

Связные графы

Отношение связности между вершинами в графе обладает тремя свойствами:

1. Рефлексивность (отражение).

Любая вершина связана сама с собой.

2. Симметричность.

Если вершина связана с вершиной , то верно и обратное: вершина связана с вершиной .

3. Транзитивность.

Если вершина связана с вершиной , а вершина связана с вершиной , то вершина связана с вершиной .

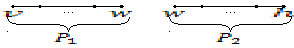
Путь, который связывает и , можно получить соединением путей и .

Отношение связности разбивает все вершины графа на компоненты связанности:

Любая пара вершин, входящая в одну компоненту связности связана. Любые вершины из разных компонент связности между собой не связаны.

Пример. Представленный граф состоит из двух компонент связности. В первой компоненте находятся вершины и , а вторая компонента включает в себя вершину .

4.3 Методы анализа графа. Поиск в ширину. Нахождение кратчайших путей в графе.

Вход алгоритма: граф и фиксированная вершина .

Выход алгоритма: компонента связности графа, в которую входит вершина .

Описание алгоритма: на этапах алгоритма строится последовательность расширяющихся множеств вершин

по следующему рекуррентному принципу: – исходная фиксированная вершина . Пусть построены множества . Тогда множество включает вершины множества , а также вершины, которые смежны с вершинами :

Таким образом, – сама вершина . – те вершины, которые достижимы из начальной вершины не более чем за один шаг. – те вершины, которые достижимы из начальной вершины не более чем за два шага…Место для формулы.

Как только два соседних множества совпадут, алгоритм завершает свою работу.

Пример.

Пусть начальная вершина – . Тогда:

Поиск в ширину позволяет находить длины кратчайших путей и сами пути. Из фиксированной вершины во все вершины графа (для простоты считаем, что граф связан).

Определение. Кратчайший путь между вершиной и – это путь, соединяющий данные вершины и содержащий наименьшее число ребер.

Утверждение. Вершины, впервые помеченные на k-ом этапе алгоритма поиска в ширину есть те вершины графа, кратчайший путь от которых до начальной вершины равен .

Доказательство:

Проведем доказательство методом индукции по номеру этапа алгоритма.

Для начального нулевого этапа утверждение очевидно. Начальная вершина множества и кратчайший путь от вершины до нее равен .

Пусть утверждение справедливо для k-ого этапа алгоритма. Докажем справедливость утверждения для -ого этапа. Так как по построению алгоритма на этапе вновь помеченные вершины есть вершины, которые смежны с вершинами, помеченными на предыдущем k-ом этапе, то из данных вершин обязательно найдется путь в вершину , содержащий не более чем ребро.

Более короткого пути, чем из k+1-ого ребра в вновь помеченные вершины на k+1 этапе бытьть не может. В последнем случае эти вершины были бы отмечены на более раннем этапе (по предположению индукции).

Утверждение доказано.

Рассмотрим более общую задачу поиска кратчайшего пути в графе, в котором каждому ребру предписано положительное число – его длина (расстояние между соответствующей парой вершин). Считаем, что это число положительное целое.

Таким образом, на вход алгоритма подается сеть и начальная вершина , где – неориентированный связный граф, а – положительная целочисленная (стоимостная) функция длины, заданная на ребрах графа.

На выходе алгоритма должны быть получены значения кратчайших путей из вершины в любую другую вершину графа . Если вершина не связана с вершиной , считаем, что расстояние равно .

Сведем рассматриваемую задачу к предыдущей задаче поиска кратчайших путей для графа, в котором функция длины единичная. Для этого совершим следующее преобразование:

Рассмотрим произвольное ребро в заданном графе. Длина данного ребра равна .

В данное ребро добавим вершину, а длину каждого полученного ребра будем считать равной .

Данное преобразование применим к каждому ребру графа. При этом длины кратчайших путей между вершинами исходного графа не изменятся, а функция длины в полученном графе единичная. Исходя из этого, можно применить алгоритм поиска в ширину для полученного графа.

Примечание. Данный алгоритм будет неэффективным в силу того, что числа в компонентах связности хранятся в двоичной системе исчисления, поэтому целое число длины будет требовать лишь битов памяти. Преобразованный граф будет требовать экспоненциальную память, по сравнению с памятью первоначального графа, т.к. ребро длины преобразуется в ребер. Если в первоначальной задаче для записи числа требуется бит, то в полученной задаче будет необходимо бит для хранения новых вершин в графе.