
- •Введение………………………………………………………………………………………..1
- •1.Элементы функциональной полноты в классе двоичных функций.
- •1.1 Основные двоичные функции и их своства. Булевой функцией f(x1 … xn) называют функцию, аргументы которой принимают значения из множества , и значение функции также из множества {0;1}.
- •Бинарная операция ассоциативна, если тождественно выполняется: ;
- •1.2 Утверждение о числе функций от n переменных.
- •1.3 Представление функции в виде совершенной дизъюнктивной и совершенной конъюнктивной формах. Разложение функции по начальному множеству переменных.
- •1.4 Утверждение о представлении двоичной функции в виде полинома Жегалкина .
- •1.5 Основные замкнутые классы двоичных функций относительно суперпозиций функций.
- •X1 x2 X
- •I этап :
- •3 Случай :
- •II этап :
- •1); 2); 3); 4).
- •1) ; 2); 3);
- •4) ; 5);
- •1.7 Предполные классы двоичных функций.
- •Все полные системы для классов t0, t1, s, m, l в утверждениях выше являются базисами для этих систем.
- •2 .Минимизация днф заданной функции.
- •2.1 Геометрическая интерпретация двоичных функций.
- •2.2 Утверждение о максимальных интервалах и тупиковых покрытиях.
- •1 Этап:
- •2 Этап:
- •2.3 Метод поиска всех максимальных интервалов заданной функции с помощью операции склеивания и сокращения.
- •2.4 Метод нахождения всех тупиковых покрытий максимальными интервалами.
- •Достаточно ясна связь задачи нахождения тупиковых покрытий и минимизации функции покрытия.
- •2.5 Метод построения сокращённой д.Н.Ф. С помощью обобщенного склеивания
- •3. Элементы математической логики. Исчисление высказываний, его полнота.
- •Семь теорем.
- •2) . Запишем аксиому а3 в следующем виде: вместоВ подставим формулу а, а вместо а подставим
- •Доказательство полноты исчисления высказываний.
- •4 Графы
- •4.1 Неориентированные, ориентированные графы. Способы задания графов.
- •Представление графов
- •1. Задание графа с помощью матрицы смежности.
- •2. Задание графа с помощью матрицы инцидентности.
- •3. Задание графа с помощью списка смежности.
- •4.2 Азбука теории графов. Маршрут, путь, простой путь. Цикл. Простой цикл. Связность в графе.
- •Связные графы
- •4.3 Методы анализа графа. Поиск в ширину. Нахождение кратчайших путей в графе.
- •4.4 Поиск в глубину. Нахождение остовного дерева с помощью поиска в глубину.
- •4.5 Укладки графов. Планарные графы.
- •Теорема Эйлера
- •4.6 Критерий Понтрягина-Куратовского планарности графа.
- •4.7 Хроматическое число графа.
- •5 Элементы комбинаторики.
- •5.1 Упорядоченные наборы с повторением и без повторений.
- •5.2 Неупорядоченные наборы элементов изданных без повторений.
- •5.3 Неупорядоченные наборы элементов изп данных с возможными повторениями.
- •5.4 Метод включения-исключения.
- •Упражнения.
- •5.5 Основы метода производящих функций.
- •1324 0100.
- •5.6 Основы теории перечисления Пойа. Лемма Бернсайда.
- •Упражнения.
- •6 Основы схем из функциональных элементов. Проблема минимизации
- •6.1 Сложность мультиплексора порядка .
- •1) Мультиплексор порядка
- •6.2 Сложность дешифратора порядка n.
- •2) Дешифратор порядка .
- •6.3 Сложность универсального многополюсника.
- •3) Универсальный многополюсник.
- •6.4 Оценка сложности функций n переменных .
- •7. Элементы теории конечных автоматов.
- •7.1 Ограниченно- детерминированные функции и автоматные языки. Эквивалентность.
- •8. Элементы теории кодирования.
- •Теория кодирования.
- •8.1 Критерий однозначности кодирования.
- •8.2 Критерий префиксного кодирования Мак-Миллана.
- •1. Можно ли выразить конъюнкцию через дизъюнкцию и отрицание.
Семь теорем.
2) . Запишем аксиому а3 в следующем виде: вместоВ подставим формулу а, а вместо а подставим
 примем
двойное отрицание А
за гипотезу, тогда по предположению
выводится
примем
двойное отрицание А
за гипотезу, тогда по предположению
выводится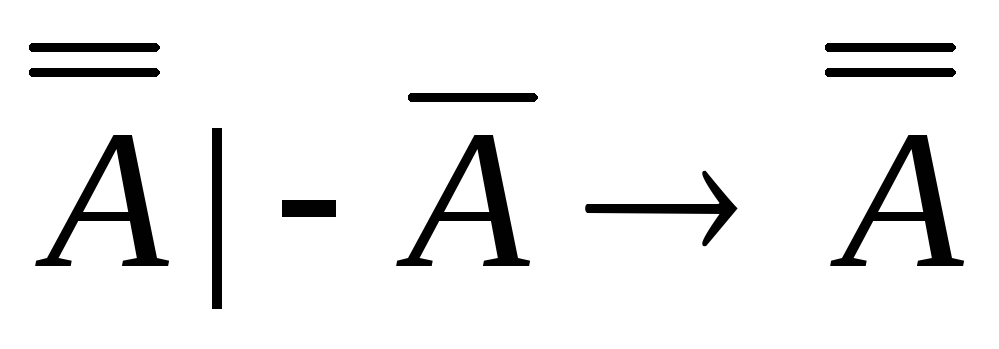 Теперь
из пунктов 1 и 2 выводится правая часть
формулы
Теперь
из пунктов 1 и 2 выводится правая часть
формулы  (теорема
1)
(теорема
1)следовательно по т1 и 3 выводится

 по
теореме дедукции
по
теореме дедукции

3)
![]() Запишем аксиому а3, подставив вместоВ
Запишем аксиому а3, подставив вместоВ
![]() ,
тогда а3=
,
тогда а3=
 по
2) и 1 выводится правая часть
по
2) и 1 выводится правая часть
принимаем А за гипотезу, тогда по пр.
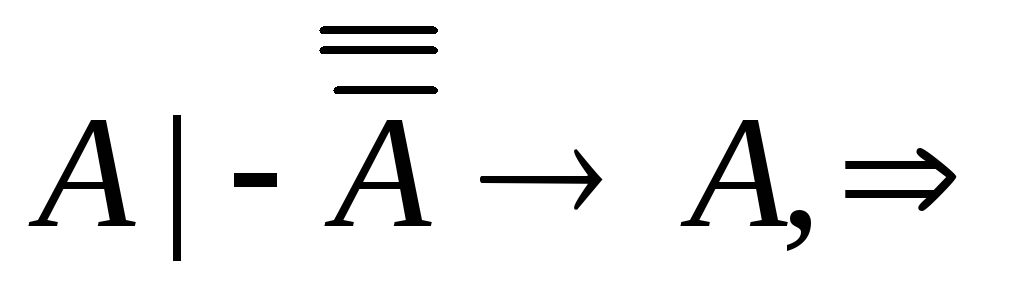 из пунктов 2, 3 по МР
из пунктов 2, 3 по МР

4)
![]() запишем третью аксиому а3
запишем третью аксиому а3


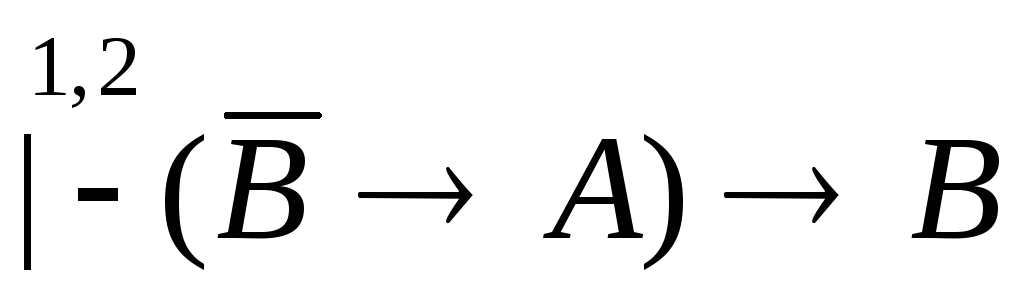
 (пр.)
(пр.)

применяя ТД второй раз получаем

5)
![]() запишем аксиому а3
запишем аксиому а3






применяя ТД дважды, получаем требуемую формулу

6)
![]()
Запишем предыдущую теорему в виде
 гипотеза
гипотеза
Примем
![]() за гипотезу, и выведем из нее посылку
за гипотезу, и выведем из нее посылку
![]() .
Тогда
.
Тогда
вывод теоремы непосредственно следует из теоремы дедукции и теоремы 5.
Чтобы
реализовать указанную цель, принимаем
![]() за
гипотезу.
за
гипотезу.
Тогда
2.
![]() ,
,![]()
![]()
3
![]()
4
из
пунктов 2,3 получаем ![]() ,
,![]() |-
|-![]()
Тогда цель выполнима по теореме дедукции из предыдущегопункта 4.
7)
![]() запишем а3
запишем а3
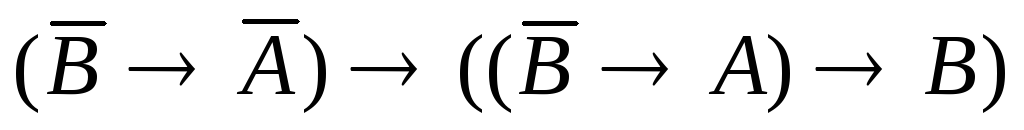
запишем 6) в следующем виде:
![]()
 по
МР, следовательно по ТД из
по
МР, следовательно по ТД из


по ТД

8)
![]() запишем а3
запишем а3

 покажем
предыдущие
покажем
предыдущие


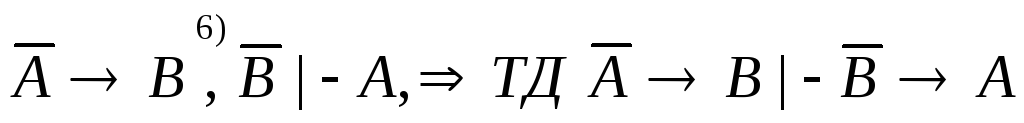 ,
таким образом второй пункт доказан
,
таким образом второй пункт доказан

 ТД
первый раз
ТД
первый раз
![]() ТД
второй раз
ТД
второй раз
Доказательство полноты исчисления высказываний.
Осталось показать, что всякая тавтология выводима в исчислении высказываний.
Лемма:
Пусть
![]() - формула от переменных
- формула от переменных![]() над связками
над связками![]() .
.
Пусть
![]() набор
значений переменных.
набор
значений переменных.![]() .
.
Покажем
из гипотез
![]()
![]()
Здесь
![]() если
если![]() ;
;![]() если
если![]()
![]() если
если
![]() ;
;![]() ,
если
,
если![]()
Доказательство
индукцией по числу связок в формуле
![]() .
.
Число
связок равно 0
![]() :
:![]()
![]() ;
;![]()
![]() Утверждение справедливо.
Утверждение справедливо.
Пусть
утверждение справедливо для любых
формул
![]() с не более чем
с не более чем![]() связками
связками![]() ;
;![]() .
.
Покажем
справедливость для F
с i+1
связкой
![]()
1.
![]() F1
и F2
– формулы с не более чем i
связками
F1
и F2
– формулы с не более чем i
связками
![]()
Рассмотрим
произвольный набор
![]() переменных
переменных![]() .
.
А)
![]()
Пусть
![]() гипотезы соответствующие набору
гипотезы соответствующие набору![]()
По индуктивному предположению :

 ;
;
 ;
;
а1.
![]() (
(
![]()
![]() )
)
1.
а1.
![]()
![]()
5.
1. (
![]()
![]() )
)![]()
![]()
![]()
![]()
![]() что
и требовалось
что
и требовалось
В)
![]()

 ;
;
 ;
;
4.
![]()
![]()
![]() что и требовалось
что и требовалось
С)
![]()
1.![]()
![]() ;
;
2.
![]()
![]() ;
;
а1.
![]()
![]()
![]() .
.
D)
![]()
1.![]()
![]() ;
;
2.![]()
![]() ;
;
7.
.
![]() (
(
![]()
![]()
![]()
что и требовалось
2.
![]()
a)
 это и естьF’
это и естьF’
b)
![]()
![]() это и естьF’
это и естьF’
Утверждение :
Любая
тавтология
![]() выводима.
выводима.
Рассмотрим
два произвольных набора значений
переменных
![]() отличающихся последней компонентой.
отличающихся последней компонентой.
Пусть
гипотезы которые соответствуют этим
наборам будут
![]() и
и![]() ,
тогда в силу предыдущей леммы и того,
чтоF
тавтология имеем:
,
тогда в силу предыдущей леммы и того,
чтоF
тавтология имеем:
![]() ;
;![]() ;
то:
;
то:![]()
![]()
По
восьмой теореме
![]() имеем
имеем![]() . В силу того что
. В силу того что![]() произвольно, точно так же можно избавиться
от
произвольно, точно так же можно избавиться
от![]() .
.
Пока
не избавимся от всех гипотез и придем
к
![]() .
.
Упражнения:
Доказать:
4 Графы
4.1 Неориентированные, ориентированные графы. Способы задания графов.
Матрица смежности, матрица инцендентностей, список смежности.
Определение.
Неориентированным
графом
называют пару ![]() ,
где
,
где ![]() – множество вершин графа,
– множество вершин графа, ![]() – множество неориентированных
ребер
графа, и последнее множество есть
некоторое подмножество множества всех
неупорядоченных пар вершин
– множество неориентированных
ребер
графа, и последнее множество есть
некоторое подмножество множества всех
неупорядоченных пар вершин ![]() .
.
![]()
Пример.
Пусть
множество вершин состоит из трех
элементов. Следовательно, неупорядоченными
парами будут следующие двухэлементные
подмножества трехэлементного множества
![]() :
:
![]()
Для графов удобно планарное представление, где вершинам графа соответствуют точки плоскости, а неориентированным ребрам соответствуют отрезки, соединяющие соответствующие пары вершин.
Пример.
Ребро, у которого оба конца являются
одной и той же вершиной, называется
петлей. В примере петлей является ребро
![]() .
.

Определение.
Ориентированным
графом
называют пару ![]() ,
где
,
где ![]() –
множество вершин графа,
–
множество вершин графа, ![]() – множество упорядоченных пар вершин
– ориентированных
ребер,
и это есть некоторое подмножество
декартова произведения
– множество упорядоченных пар вершин
– ориентированных
ребер,
и это есть некоторое подмножество
декартова произведения ![]() :
:
![]()
Пример.
Множество
вершин состоит из трех элементов ![]() .
Тогда упорядоченными парами вершин
будут следующие:
.
Тогда упорядоченными парами вершин
будут следующие:
![]()
Для ориентированных графов удобно планарное представление, где вершинам соответствуют точки плоскости, а ребрам соответствуют ориентированные линии, которые соединяют в определенном направлении соответствующие пары вершин.
Пример.
Ориентированное
ребро, у которого оба конца являются
одной и той же вершиной, называется
петлей. В примере петлей является ребро
![]() .
.

