1. Собственные колебания груза на пружине

Будем полагать, что вся масса m рассматриваемой системы (рис.43) сосредоточена в грузе; пружина обладает идеальной упругостью и, следовательно, закон Гука для неё в точности выполняется. Ось направим вертикально вниз. Координату груза, когда он находится в состоянии равновесия, примем равной нулю. Как видно из рисунка 43,

Рис.43

смещению груза вверх соответствуют отрицательные координаты, смещению вниз – положительные.

Составим дифференциальное уравнение колебаний груза. Дифференциальное уравнение механического движения вообще – это, в сущности, математическое выражение второго закона Ньютона, формула, связывающая массу тела, действующую на него силу и ускорение, приобретаемое телом под действием этой силы. Однократное интегрирование этого уравнения дает зависимость от времени скорости, двукратное – координат (последняя зависимость называется интегральным законом движения).

Колебания груза на пружине в отсутствие трения происходит под действием упругой силы. Для изображенного на рисунке 43, б положения имеем: .

Величина k называется жёсткостью пружины. Жёсткость численно равна упругой силе, возникающей в пружине при единичном растяжении или сжатии её. Жёсткость пружины зависит от материала пружины и её геометрии – формы, диаметра витков, густоты витков, длины пружины и т.д.

Сила сообщает грузу ускорение.

По второму закону Ньютона или , илиРазделив обе части последнего уравнения наи введя обозначение(в соответствие с (22.5)), получим искомое дифференциальное уравнение собственных гармонических колебаний:

(22.7)

Общее решение этого линейного однородного дифференциального уравнения имеет вид:

(22.8)

где и- амплитуда колебаний и начальная фаза.

Найдём период колебаний груза. По (21.5) , но,Следовательно,(22.9)

Частота колебаний (22.10)

Итак, чем больше масса груза и чем меньше жесткость пружины, тем медленнее происходят колебания. Существенно отметить, что период и частота колебаний не зависят от амплитуды.

Амплитуда иначальная фаза собственных незатухающихгармонических колебанийзависят от начальных условий – параметров состояния в начальный момент времени: от и. Положивв формулах (22.8) и (21.7) , получим выражения дляи:

Откуда 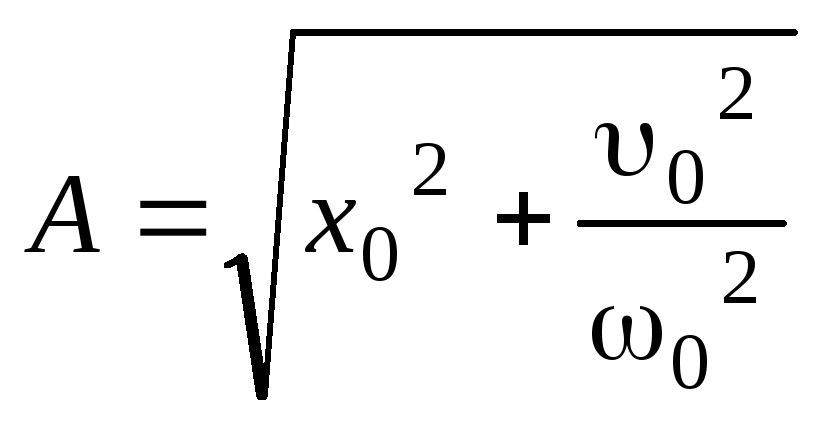(22.11)

и

(22.12)

2. Колебания математического маятника

Математический маятник (рис.44) представляет собой материальную точку, подвешенную на невесомой и нерастяжимой нити.

Реальным приближением к математическому маятнику может служить небольшой шарик, подвешенный на тонкой длинной нити. Отклонение маятника от положения равновесия будем характеризовать

углом (рис.44). Формула, выражающая зависимость этого угла от

времени, и будет представлять собой закон движения маятника.

При отклонении маятника от положения равновесия возникает вращательный момент , модуль которого равен, где- масса маятника,- его длина. Направление этого момента таково, что он стремится вернуть маятник в положение равновесия, т.е. по своему действию он аналогичен квазиупругой силе. Поэтому так же, как координатеи проекции силыприписываются противоположные знаки, противоположные знаки следует приписать вращательному моментуи угловому смещению. Следовательно, выражение для вращательного момента будет иметь вид:

. (22.13)

Вращательный момент, действующий на маятник, сообщит маятнику угловое ускорение. По основному уравнению динамики вращательного движения, где- момент инерции маятника, равный. Угловое ускорение равно второй производной от углового смещения по времени:. Учитывая это, можно записать:

(22.14)

Ограничимся рассмотрением малых колебаний. При малых углах можно заменить на:.

Тогда вращательный момент будет равен:

.

Подставив это выражение в основное уравнение движения (22.14), по-

лучим:

или (22.15)

Обозначив , найдем искомое дифференциальное уравнение движения маятника

(22.16)

Решение этого уравнения имеет вид:

, (22.17)

т.е. малые колебания математического маятника являются гармоническими. Период этих колебаний

, (22.18)

частота

. (22.19)