Проверим полученный опорный план на невырожденность.
Подсчитаем число занятых клеток таблицы, их 5, а должно быть m + n - 1 = 5. Следовательно, опорный план является невырожденным.
Найдем потенциалы опорного решения.
Ui, Vi. по занятым клеткам таблицы, в которых Ui + Vi = Сij, полагая, что u1 = 0;
Получим v1=20; v2=30; v3=50; v4=0; u2= -10
Ui Vi |
v1=20 |
v2=30 |
v3=50 |
v4=0 |
u1=0 |
20 (1000) |
30 (800) |
50 (1600) |
0 (800) |
u2= -10 |
60 |
20 (1200) |
40 |
0 |
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию Ui + Vi <= Сij.
При этом грузооборот составит:
Q = 20*1000 + 30*800 + 50*1600 + 0*800 + 20*1200 = 148000 тон/км.
Обоснование результата
Так как затраты на перевозку 1 т продукта на 1 км составляют 25 д.е., то денежные затраты составляют:
S = 148000*25 = 3700000 д.е.
4. Решение в программе tora
Программа TORA реализует решение задач линейного программирования.
В данной курсовой работе программа TORA используется для решения транспортной задачи методом наименьшего элемента.
Чтобы решить данную транспортную задачу, запускаем программу Tora.exe, в главном меню программы выбираем Transportation model (Транспортная модель).
Далее, выбираем необходимое количество ограничений и переменных (см. рисунок 1).
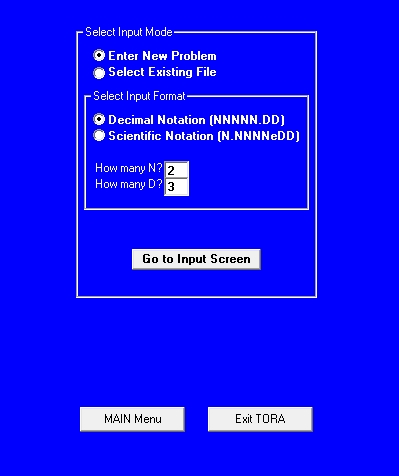
Рис.1 Заполнение переменных
Теперь нужно ввести все значения переменных в созданную таблицу (см. рисунок 2).
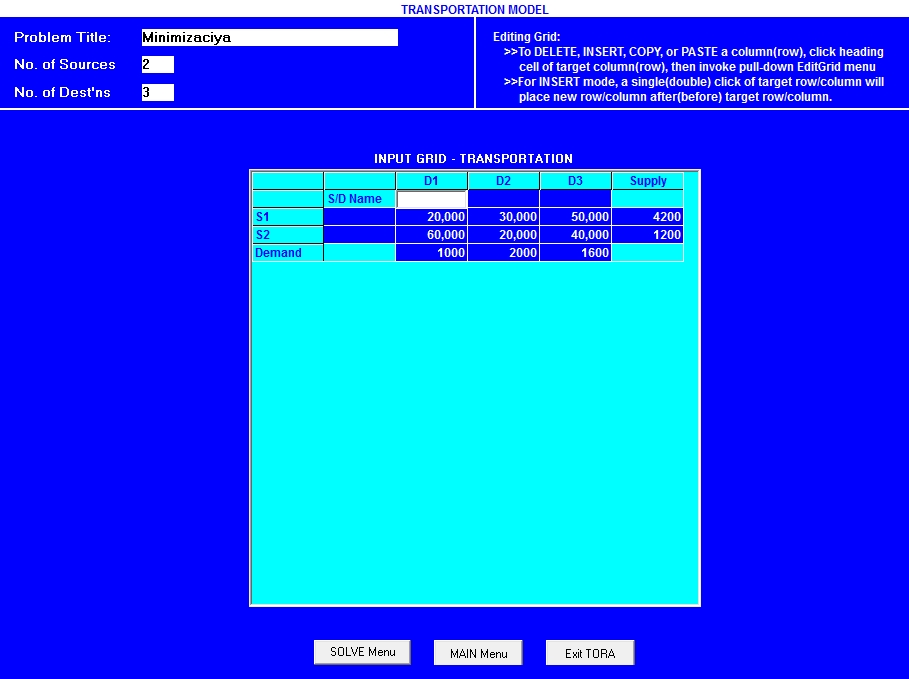
Рис.2 Заполнение таблицы
Когда данные будут введены, нажимаем кнопку «SOLVE Menu» и выбираем метод Solve Problem => Iterations => Least-Cost starting solution (Метод наименьшего элемента) с помощью которого необходимо решить задачу.
Далее, появиться оптимальное решение транспортной задачи (см. рисунок 3).
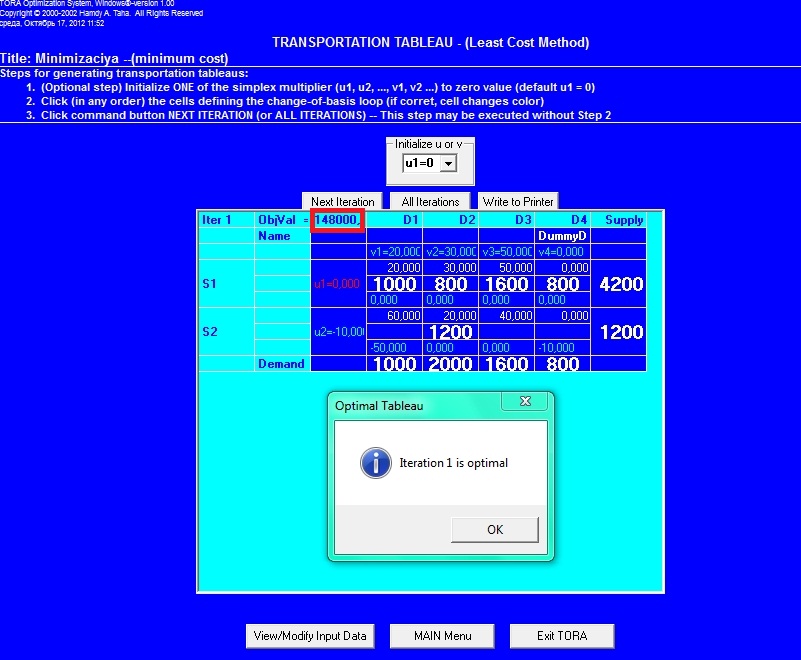
Рис.3 Оптимальное решение
Как видно из решения программы грузооборот составит:
Q = 148000 тон/км.
Рассчитаем перевозки зерна из условия минимизации транспортных расходов.
Так как затраты на перевозку 1 т продукта на 1 км составляют 25 д.е., то денежные затраты составляют:
S = 148000*25 = 3700000 д.е.
5. Решение в программе msExcel.
Мощным средством анализа данных MSExcel является надстройка Solver (Поиск решения). С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для расчета заданного значения применяются различные математические методы поиска. Программа Поиск решений (в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных задач оптимизации. Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями:
количество неизвестных (decision variable) – 200;
количество формульных ограничений (explicit constraint) на неизвестные – 100;
количество предельных условий (simple constraint) на неизвестные – 400.
Для решения данной транспортной задачи будем проводить MSExcel 2007.
Запустим файл «TZ.xlsm». После запуска файла нужно включить макросы «Параметры» => «Включить содержимое» (см. рисунок 4).
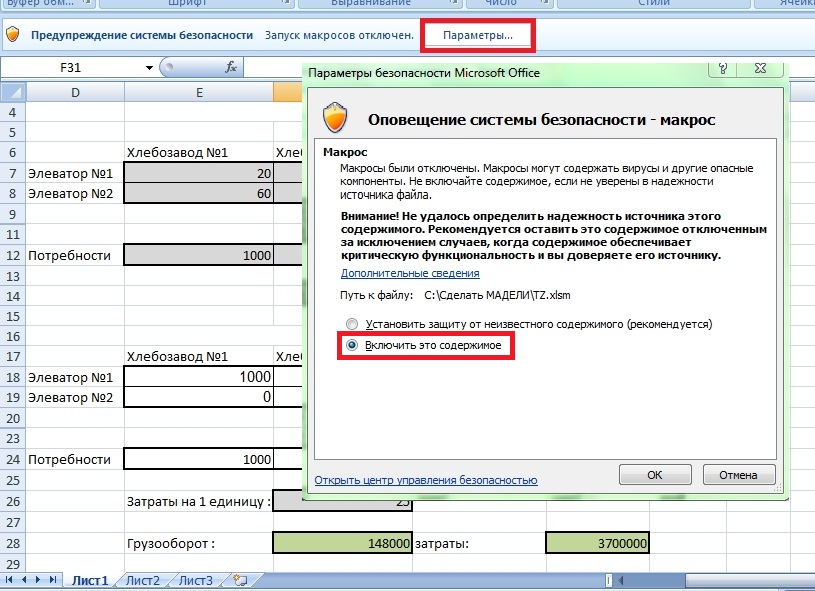
Рис.4 Включение макросов
По умолчанию в MSExcel 2007 надстройка «Поиск решения» отключена. Чтобы активизировать ее необходимо перейти на вкладку «Пуск », нажать кнопку «Параметры Ecxel» => «Надстройки» и установить флажок рядом с пунктом «Поиск решения». Нажать «ОК» (см. рисунок 5).
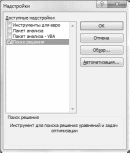
Рис.5 Надстройки «Поиск решения»
Далее переходим к вводу данных задачи.
В ячейки «E7-G8» вводим расстояния до хлебозаводов, в ячейки «E12-G12» вводим потребности хлебозаводов, в «I7;I8» вводим запасы в элеваторах и в ячейку «F26» вписывается значение затрат на 1 единицу. В ячейки «H7» и «H8» вставляем нули, так как данная задача несбалансированна и запасы превышают потребности и вводится фиктивный потребитель, ячейка «H12» считается автоматически, как только будут заполнены ячейки с потребностями и запасами «=(I7+I8)-(E12+F12+G12)» (см. рисунок 6).
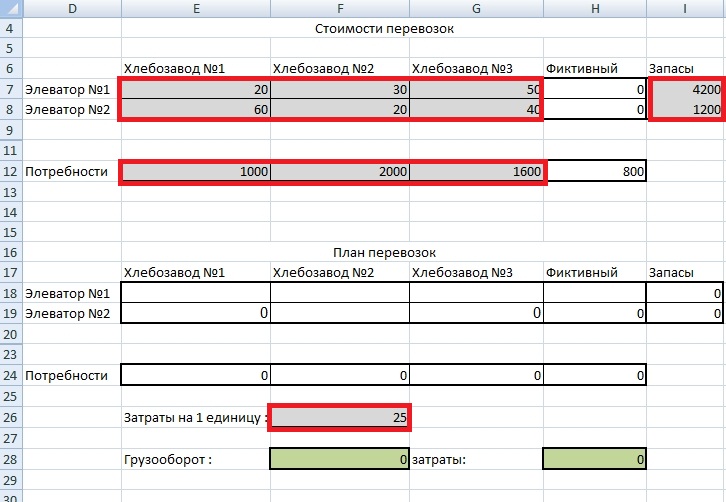
Рис.6 Ввод данных
На вкладке «Данные» нажимаем надстройку «Поиск решения» (см. рисунок 7).
Устанавливаем целевую ячейку «F28», так как нам нужно найти минимальные затраты ставим галочку на «Минимальное значение»
Расчеты и изменения будут происходить в ячейках «E18-H19», поэтому и указываем эти ячейки в графе «Изменения ячейки»
Необходимо указать ограничения:
В ячейках «E18-H19 »введем параметр > 0, так как оптимальный план не может иметь отрицательных значений.
«I18;I19» <= «I7;I8»,
«E24;H24» = «E12;H12».
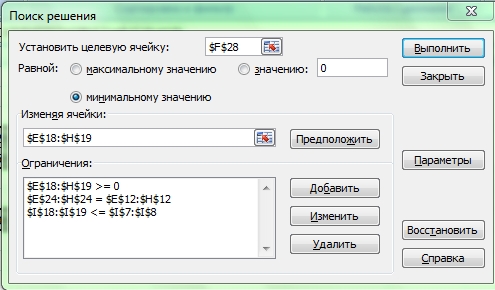
Рис.7 Параметры функции «Поиск решения»
После того, как выставлены все ограничения, нажимаем на кнопку «Выполнить». Программа рассчитает оптимальный грузооборот и выведет его в ячейку «F28». А в ячейку «H28» будут минимальные расходы на грузоперевозки (см. рисунок 8).
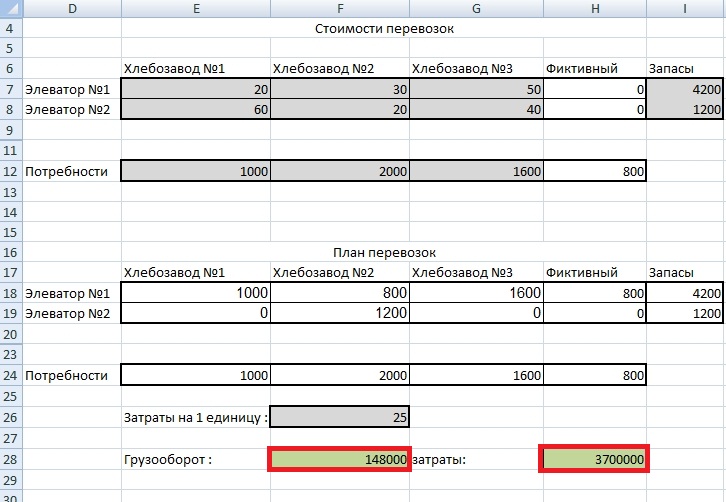
Рис.8 Результат расчетов
Если необходимо изменить исходные данные и пересчитать целевую функцию - можно воспользоваться макросом для поиска решения, нажав на сочетание клавиш Alt+F8 выполнить «Makros1».
Как видно из ячейки «F28» грузооборот составит:
Q = 148000 тон/км.
А в ячейке «H28» рассчитаются денежные затраты :
S = 3700000 д.е.
.