4. Найти потенциалы опорного решения.

Метод потенциалов предназначен для окончательной оптимизации решения транспортной задачи.

Если допустимое решение 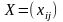, i=1,2,…,m; j=1,2,…n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков 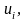i=1,2,…,m и потребителей 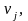j=1,2,…,n, удовлетворяющее следующим образом:

Группа равенств (2.1) используется как система уравнений для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных i=1,2,…,m и j=1,2,…,n. Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n-1. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы.

Группа неравенств (2.2) используется для проверки оптимальности опорного решения. Эти неравенства удобнее представить в следующем виде:

(2.3)

Числа называются оценками для свободных клеток таблицы (векторов условий) транспортной задачи.

Опорное решение является оптимальным, если для всех векторов условий (клеток таблицы) оценки неположительные.

Оценки для свободных клеток транспортной таблицы используются при улучшении опорного решения. Для этого находят клетку (l,k) таблицы, соответствующую . Если , то решение оптимальное. Если же , то для соответствующей клетки (l,k) строят цикл и улучшаю решение, перераспределяют груз

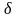
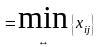по этому циклу;

5. Обоснование результата.

3. Решение задачи вручную

1. Проверим на сбалансированность.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов:

Элеватор	Хлебозавод				Запасы зерна
	1	2	3
1	20	30	50	4200
2	60	20	40	1200
Потребность в зерне	1000	2000	1600

Запасы зерна на элеваторах :

∑ A_i = 4200 + 1200 = 5400

Потребность в зерне хлебозаводов:

∑ B_i = 1000 + 2000 + 1600 = 4600

Так как ∑ A_i > ∑ B_i, то вводим «Фиктивный» пункт потребления – хлебозавод №4 с потребностью в зерне :

B4 = ∑A_i - ∑B_i = 5400 – 4600 = 800 т. и с нулевыми расстояниями до элеваторов.

Занесем исходные данные в распределительную таблицу.

	B1	B2	B3	B4	∑Ai
A1	20	30	50	0	4200
A2	60	20	40	0	1200
∑ Bi	1000	2000	1600	800	5400

2. Отыщем начальное решение. Методом минимального элемента.

Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	B1	B2	B3	B4	∑ Ai
A1	20 (1000)	30 (800)	50 (1600)	0 (800)	4200
A2	60	20 (1200)	40	0	1200
∑ Bi	1000	2000	1600	800	5400

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.