Содержание

1. Постановка задачи 3

2. Описание алгоритма решения задачи 4

3. Решение задачи вручную 7

4. Решение в программе TORA 10

5. Решение в программе MSExcel. 13

6. Разработка программы для решения задачи в общем виде (Delphi) 18

7. Выводы 28

Список используемой литературы 29

1. Постановка задачи

1. Выбрать и обосновать наиболее эффективный метод решения задачи.

2. Разработать алгоритм и программу для решения задачи в общем виде.

3. Проверить правильность алгоритма на предлагаемой задаче.

4. Задача:

Имеются два элеватора, в которых сосредоточено соответственно 4200 и 1200 т зерна. Зерно необходимо перевезти трем хлебозаводам в количестве 1000,2000,1600 т каждому. Расстояние от элеватора до хлебозаводов указано в следующей таблице:

Элеваторы	Хлебозаводы
	1	2	3
1 2	20 60	30 20	50 40

Затраты на перевозку 1 т продукта на 1 км составляют 25 д.е.

Спланируйте перевозки зерна из условия минимизации транспортных расходов.

2. Описание алгоритма решения задачи

Так как рассматриваемая задача является транспортной, то алгоритм решения будет выглядеть следующим образом:

1. Проверить на сбалансированность.

Транспортная задача является сбалансированной, если суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

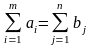.Если суммарные запасы поставщиков превосходят суммарные запросы потребителей, т.е.

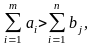то необходимо ввести фиктивного (n+1)-го потребителя с запросами равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза;

2. Определить начальное решение.

Найдем начальное решение методом наименьшего элемента, который позволяет построить опорное решение, достаточно близко к оптимальному.

Опорным решением транспортной задачи называется любое допустимое решение, для которого векторы условий, соответствующие положительным координатам, линейно независимы.

Данный метод позволяет построить опорное решение, которое достаточно близко к оптимальному, так как использует матрицу стоимостей транспортной задачи 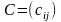, i=1,2,…,m; j=1,2…,n. Данный метод состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости 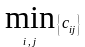, и исключается из рассмотрения только одна строка(поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют также. Поставщик исключается из рассмотрения, если его запасы заканчиваются. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик не исключен, но его запасы равны нулю, то на том шаге, когда от него требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично поступают с потребителем;

3. Проверить полученный опорный план на невырожденность.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n - 1.Опорный план - невырожден, если число ненулевых перевозок равно n+m-1, поэтому и первоначальный план также должен удовлетворять этому требованию;