Лекции по ТАУ2 / Лекция №6-2

Амплитудные частотные характеристики замкнутой

системы

1) Пусть частотная передаточная функция разомкнутой системы

,

(идеальное интегрирующее звено).

Передаточная функция замкнутой системы по возмущению

.

Идеальное интегрирующее звено, охваченное жесткой единичной обратной связью, имеет передаточную функцию апериодического звена.

2) Идеальное (пропорциональное) звено.

,

,

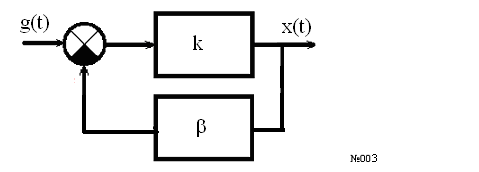
β – коэффициент обратной связи.

При β=1 и . Сигнал на выходе

3) Инерционное интегрирующее звено.

.

Передаточная функция замкнутой системы по возмущению

.

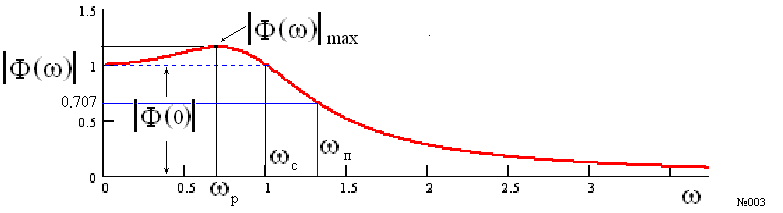
Амплитудная частотная характеристика замкнутой системы

Величина

называется показателем колебательности системы. Отметим, что обычно . Этот показатель характеризует качество переходного процесса в замкнутой системе и обычно лежит в пределах 1.1..1.5, хотя в некоторых случаях допускается величина до 2..2.5.

На рисунке:

ω_р – резонансная частота;

ω_с - частота среза (при ω>ω_c амплитуда сигнала на выходе системы меньше амплитуды входного сигнала);

ω_п – полоса пропускания системы.

Дифференциальное уравнение замкнутой

системы

Частотная передаточная функция разомкнутой системы:

.

Частотна передаточная функция по задающему воздействию:

.

Передаточная функция замкнутой системы

,

.

Рассмотрим частный случай.

Частотная передаточная функция разомкнутой системы:

.

Производя замену jω→p, получим

.

После очевидных преобразований приходим к дифференциальному уравнению замкнутой системы:

,

Рассматриваемая система описывается дифференциальным уравнением третьего порядка.

Можно записать уравнение в виде

Полагая g₁(t)≡0 получаем характеристическое уравнение (характеристический многочлен) замкнутой системы:

,

.

Корни характеристического уравнения определяют свободное движение системы.

Правило Ишлинского :

Если в замкнутой системе высокого порядка между входной и выходной величиной существует единичная обратная связь, то в первом приближении эта система ведет себя как система второго или третьего порядка.

Поэтому особенное внимание в дальнейшем будет уделяться системе третьего порядка с единичной обратной связью.

Диаграмма Вышнерадского

Диаграмма дает полное представление о влиянии расположения корней характеристического уравнения на вид переходного процесса в системе третьего порядка.

В общем случае характеристическое уравнение системы

.

Разделим на a₃

и введем новую переменную

.

Обозначив , получим

.

Преобразования позволили сократить число коэффициентов характеристического уравнения до двух и изобразить характерные области на плоскости AB:

Желтая зона – зона неустойчивости системы третьего порядка.