
Решение:
Дана многофакторная
(сложная) аддитивная модель Х=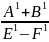 ;
;
Критерии ранжирования: из количественных сначала анализируются факторы - условий производства, а затем - факторы, характеризующие результат деятельности; при аддитивной зависимости факторы анализируются одновременно.
Число первичных факторов n=4(А, В, E, F), входящих в аналитическую формулу расчета результативного показателя (РП);
Число параметров факторной системы: (n+1)=4+1=5 (А, В, E, F, Х);
Информационная база представлена не в полном объеме, необходимые значения можно определить с помощью расчета
Цель анализа: относительное изменение Х от влияния фактора В и F;
абсолютное изменение РП Х от влияния фактора А; на сколько процентов и как изменится уровень РП Х от влияния факторов А и Е при заданных условиях;
определение доли (степени) влияния факторов, отражающих результаты деятельности в общем изменении РП Х.
Первичный фактор В находится в прямой аддитивной зависимости с РП Х.
mХ(В)=2
св.ов.=
mБ(В)*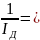 [Х=
[Х=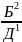 ∕∕
∕∕
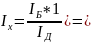 add=
mВ*
add=
mВ*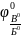 *
*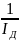 =3-х к.ф=
=3-х к.ф=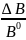 *102*
*102*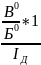 =
=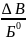 *102*
*102*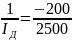 *102*
*102*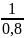 =-10%
=-10%
mХ(В)=3-х
к.ф. (1 сп.)= 2=add=
2=add=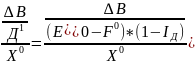 =
=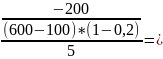 -10%
-10%
mХ(В)=3-х
к.ф. (2 сп.)=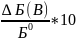 2*
2*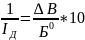 2*
2*
Дано:
Б=А2+В2
Найти: mХ(В), ±∆Х(А), mХ(mF=50%), mХ(А), mХ(Е),
|
0 |
1 |
∆ |
m |
Б |
2500 |
|
|
-28% |
Д |
|
|
|
-20% |
В |
|
|
-200 |
-40% |
Х |
5 |
|
|
|
А |
|
1500 |
|
|
Схема взаимозависимости:
Х
1
2
2
1
1
1
Б2
А2
В2
Д1
Е1
F1
Каналы влияния:пр.add
пр. mult
В
Б Х
А
Б=А2+В2
обр. add
обр. mult
F
Д Х
пр. add
обр. mult
Е
Д Х
Первичный фактор А находится в прямой аддитивной зависимости с РП Х.
ЦП
=
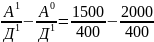 =-1,25
=-1,25
разниц
=
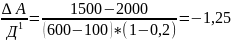
±
3-х
к.ф. =
* =
=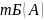 *
*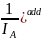 =
=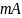 *
*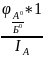 =
=
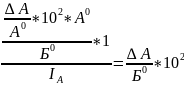 *
*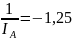
корр. ≠ [т.к. add зависимость]
mХ(mF=50)=3-х
к.ф.=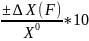 2=ДУ.
обр.add=[
2=ДУ.
обр.add=[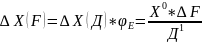 ]=-Х0*
]=-Х0*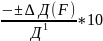 2=-5*
2=-5*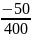 *102
*102
mХ(А)=
3-х к.ф.=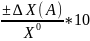 2=разниц=
2=разниц=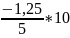 2=-25%
2=-25%
mХ(Е)
= 1
св.ов.=mД(Е)=add=-mЕ*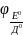 =
=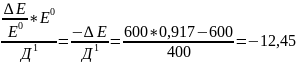

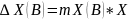 0*100=-10*5*10-2=-0,5
0*100=-10*5*10-2=-0,5
