Д

№1

ано:

К=А¹*b²

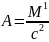
М=Д¹*р²

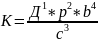
Найти:

±∆К(М), ±∆К(с), ±∆К(р), mК(М), mК(с), mК(р).

Схема взаимозависимости:

К

2

1

А

2

2

1

1

М

Д¹

с³

р²

b⁴

Каналы влияния

М

К=А¹*b²

А К

С

кр. mult

кр. mult

кр. mult

р

М=Д¹*р²

К=А¹*b²

М А К

Решение:

Дана многофакторная (сложная) мультипликативная модель К=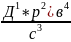

Критерии ранжирования: количественные факторы анализируются раньше качественных; качественные факторы среди последнего рассматриваются в 1-ю очередь.

Число первичных факторов n=4(Д, р, с, в), входящих в аналитическую формулу расчета результативного показателя;

Число параметров факторной системы: (n+1)=4+1=5 (Д, р, с, К);

Количество этапов детализации n-1=4-1=3.

Информационные данные в полном объеме: по 2-м значениям ( в базисном и анализируемом периодах) для каждого фактора и результативного показателя и темпы роста.

С

ЦП=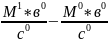 = =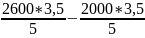420

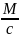убфактор М входит в субсистему А= , тип зависимости - обратная mult => для оценки влияния фактора М на результативный показатель К можем использовать следующие способы последовательного элиминирования - цепных подстановок, разниц, способ корректировок.

разниц = ∆А(М)*в⁰ =

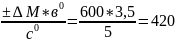
±∆К(М)=

К^0*(I_м-1) - [ влияние любого количественного фактора М на изменение результативного показателя К определяется как произведение темпа роста (I_м-1) на базисную величину результативного показателя К⁰ ]

±∆К(М)=

корр

3-х к.ф.

mК(М) =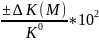 - [формула зависимости 3-х параметров (абсолютное, относительное изменения результативного показателя от влияния отдельно взятого фактора и базисное значение результативного показателя)]

mК(М) =

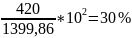
Дано:

К=А¹*b²

М=Д¹*р²

Найти:

±∆К(М), ±∆К(с), ±∆К(р), mК(М), mК(с), mК(р).

Схема взаимозависимости:

К

2

1

А

2

2

1

1

М

Д¹

с³

р²

b⁴

Каналы влияния

М

К=А¹*b²

А К

С

кр. mult

кр. mult

кр. mult

р

М=Д¹*р²

К=А¹*b²

М А К

Аналитическая проверка:

- по 3-х к.ф.

≡ =

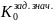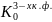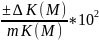
1399,86 ≡ 1400

• ≡ , что свидетельствует об адекватности полученных результатов влияния фактора М на результативный показатель К.

Первичный фактор с находится в кратной mult зависимости с К. При данном типе зависимости можно использовать следующие методы последовательного элиминирования: способ ЦП, способ корректировок.

ЦП = 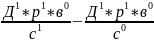[влияние любого фактора на изменение результативного показателя определяется как разность 1-ой и 2-ой подстановок. В 1-ой подстановке уровень анализируемого фактора берется фактически, а во 2-ой базисным. Уровень каждого из остальных факторов в обеих подстановках одинаков - фактический, если они по установленным рангам предшествуют данному фактору, и базисный - для факторов, следующих (по рангам) после этого конкретного фактора. По схеме взаимозависимости видно, что первичные факторы Д, р предшествуют анализируемому фактору с и следующие берутся по фактическому уровню в обе подстановке , а первичный фактор в берется на базисном уровне, т.к. следует после анализируемого фактора с.]

±∆К(с)=

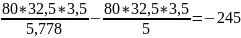
±∆К(с)=

разниц ≠ [т.к. обратная зависимость]

корр. = К⁰(I_А-I_М) [Выделим из общей модели результативного показателя субмодель (простую, 2-х факторную), которая включает данный качественный показатель , имеющий результативный показатель и количественный фактор: А= 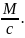Влияние любого качественного фактора определяется как произведение базисной величин К⁰ общей модели на разность коэффициентов I_А и количественного фактора I_М субсистемы]

±∆К(с)=

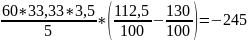
Дано:

К=А¹*b²

М=Д¹*р²

Найти:

±∆К(М), ±∆К(с), ±∆К(р), mК(М), mК(с), mК(р).

Схема взаимозависимости:

К

2

1

А

2

2

1

1

М

Д¹

с³

р²

b⁴

Каналы влияния

М

К=А¹*b²

А К

С

кр. mult

кр. mult

кр. mult

р

М=Д¹*р²

К=А¹*b²

М А К