17. Кільця і поля.

Означення. Кільцем називається непорожня множина 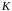, на якій визначені дві бінарні алгебраїчні операція + (додавання) і (множення) так, що виконуються наступні умови (аксіоми кільця):

К1. 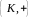– абелева група:

1. операція + асоціативна: ;

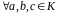
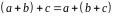2. в множині існує нульовий елемент : ;

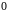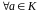
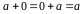3. для кожного елемента 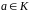існує протилежний елемент :

.

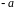4. операція + комутативна: .

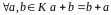К2. 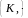– півгрупа:

5. операція асоціативна: ;

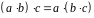К3. Операція (множення) дистрибутивна зліва і справа відносно операції +(додавання):

6. ;

;

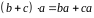Кільце позначається 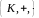або просто .

Означення. Полем називається комутативне кільце, елементи якого, відмінні від нульового елемента утворюють групу відносно операції .

Приклад.

1. – поле раціональних чисел.

2. – поле дійсних чисел.

3. – поле комплексних чисел.

18. Гратки.

19. Булеві змінні і функції.

Елементами булевої алгебри є булеві константи, булеві застосування і булеві операції. Існують дві булеві константи, які прийнято позначати 0 і I. Ці константи не розглядаються як числа і для їх позначення можна використовувати будь-які слова (наприклад, так і ні. Істина і брехня, true і false і т.д.). Булеві змінні можуть приймати лише значення булевих констант, тобто 0 або 1. Таким чином, змінна х l називається булевої змінною, якщо і тільки якщо .

Бу́лева фу́нкція (функція алгебри логіки, логічна функція) — в дискретній математиці відображення Bⁿ → B, де B = {0,1} — булева множина.

Bⁿ — множина всіх можливих послідовностей з 0 та 1 довжини n.

Булева функція задається у вигляді таблиці, або графіка зі стандартним (лексикографічним) розташуванням наборів аргументів.

В стандартному розташуванні набори можна розглядати як двійкові записи цілих чисел від 0 до . Функцію, задану зі стандартним розташуванням наборів, можна ототожнити з набором довжини .

Очевидно, що множина всіх можливих наборів довжини , тобто множина n-арних булевих функцій, складається з елементів. При n=0 це 2, при n=1 — 4, при n=2 — 16, при n=3 — 256 тощо.

Нуль-арними булевими функціями є сталі 0 і 1.

Функції 0 і 1 називаються тотожними нулем і одиницею, функція x — тотожною, — запереченням. Замість виразу вживається ще вираз . Ці вирази читаються як «не x».

Подамо також деякі з 16 бінарних функцій разом із їх позначеннями:

Функція, позначена виразом , називається кон'юнкцією і позначається ще як x&y, або xy. Усі ці вирази читаються як «x і y».

Зауважимо, що інфіксні позначення наведених функцій вигляду x f y, де f — відповідний знак, склалися історично. Їх так само можна позначати й у вигляді f(x, y), наприклад, .

20. Способи задання булевих функцій.

Булеві функції можуть задаватися наступними способами:

1) За допомогою таблиці істинності (значення якої беруться з

інтерпретацій).

2) Порядковим номер, який має ця функція.

3) Аналітично (у вигляді формули).

Таблиця, в якій кожній інтерпретації функції поставлена у відповідність

її значення, називається таблицею істинності булевої функції.

Кількість булевих функцій двох змінних f(x, y) дорівнює

222 =16.

Більшість з 16-ти булевих функцій f(x, y) часто застосовують на практиці,

мають різні значення.

21. Двоїстість.

Поняття двоїстості є однією з тих концепцій, які з успіхом використовуються у

найрізноманітніших галузях математики. Ми розглянемо двоїстість на простішому прикладі

булевих функцій.

Означення 10.1. Нехай f(x1,…,xn)IPn – булева функція. Тоді функція

f *(x1,…,xn) = ( ,..., ) 1 n f x x

називається двоїстою функцією до f.

З означення випливає, що двоїста функція інволютивна: f ** = f, а відношення “бути

двоїстою до” на множині булевих функцій симетричне, тобто якщо f * = g, то g * = f.

Якщо в таблиці істинності булевої функції f інвертувати всі значення, то отримана

таблиця буде таблицею істинності двоїстої функції f *.

Наприклад

x y xUy
0 0 0
0 1 0
1 0 0
1 1 1
x y (xUy)*
1 1 1
1 0 1 =
0 1 1
0 0 0
x y (xUy)*
0 0 0
0 1 1
1 0 1
1 1 1

Таким чином можна визначити двоїсту функцію до будь-якої булевої функції.

Наведемо приклади інших двоїстих функцій:

_ функція 0 двоїста 1;

_ функція 1 двоїста 0;

_ функція кон’юнкції xUy двоїста диз’юнкції xUy;

_ функція диз’юнкції xUy двоїста кон’юнкції xUy.