25

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

«Кривые второго порядка»

Учебно-методическое пособие по специальности «Химия» 020101 (011000).

ВОРОНЕЖ

2005

Утверждено научно-методическим советом математического факультета

31 Августа 2005 года

Протокол №1

Составитель Петрова Е.В.

Учебно-методическое пособие подготовлено на кафедре

уравнений в частных производных и теории вероятностей

математического факультета Воронежского

госуниверситета

Рекомендуется для студентов 1 курса дневного отделения

химического факультета

Кривые второго порядка

Уравнение F(x;y)=0 определяет кривую второго порядка, если хотя бы одна из переменных в этом уравнении имеет вторую степень.

1. Окружность

Окружность – множество всех точек плоскости, равноудаленных от данной точки (центра). Если r – радиус окружности, а точка C (a;b) – ее центр, то уравнение окружности имеет вид

. (1)

В частности, если центр окружности совпадает с началом координат, то последнее уравнение примет вид

. (2)

Если в левой части уравнение (1) раскрыть скобки, то получится уравнение вида

, (3)

где .

В общем случае уравнение (2) определяет окружность, если .

Если , то указанное уравнение определяет точку , а если , то оно не имеет геометрического смысла. В этом случае говорят, что уравнение определяет мнимую окружность.

Полезно помнить, что уравнение окружности содержит старшие члены и с равными коэффициентами, и в нем отсутствует член с произведением x на y.

Взаимное расположение точки M(x₁;y₁) и окружности определяется такими условиями: если , то точка М лежит на окружности; если , то точка М лежит вне окружности, и если , то точка М лежит внутри окружности.

Уравнение

(4)

представляет окружность при условии, что коэффициенты A, B, C, D удовлетворяют неравенству

(5)

Тогда центр (a;b) и радиус R окружности можно найти по формулам

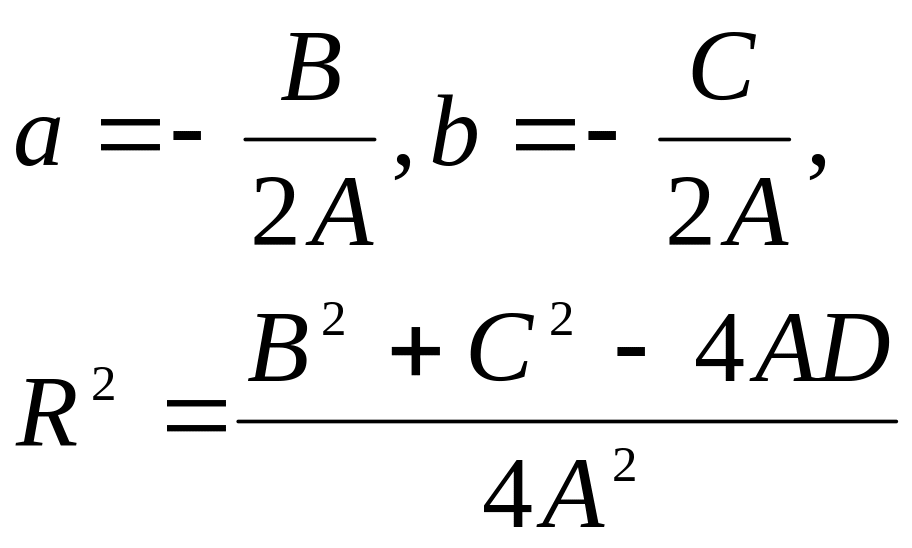(6)

Пример 1. Найти координаты центра и радиус окружности .

Решение.

Первый способ.

Уравнение подходит под вид (4); здесь

A=5, B=-10, C=20, D=-20.

По формулам (6) находим:

,

т.е. центр есть (1;-2), а радиус R = 3.

Второй способ:

Разделив уравнение на коэффициент при членах второй степени, т.е. на 5, получим:

.

Дополним суммы и до квадратов. Для этого прибавим к первой сумме 1, а ко второй 4. Для компенсации прибавим те же числа к правой части уравнения. Получим:

,

т.е. .

Пример 2. Составить уравнение окружности, описанной около треугольника, стороны которого заданы уравнениями , , .

Решение.

Найдем координаты вершин треугольника, решив совместно три системы уравнений:

В результате получим A(3;-7), B(5;2), C(-1;0).

Пусть искомое уравнение окружности имеет вид . Для нахождения a, b и r напишем три равенства, подставив в искомое уравнение вместо текущих координат координаты точек A, B и C:

; ; .

Исключая , приходим к системе уравнений

или

Отсюда a=3,1, b=-2,3. Значение находим из уравнения , т.е. . Итак, искомое уравнение записывается в виде .

Пример 3. Составить уравнение окружности, проходящей через точки A(5;0) и B(1;4), если ее центр лежит на прямой .

Решение.

Найдем координаты точки М – середины хорды АВ; имеем , , т.е. М(3;2). Центр окружности лежит на серединном перпендикуляре к отрезку АВ. Уравнение прямой АВ имеет вид

, т.е. .

Так как угловой коэффициент этой прямой есть -1, то угловой коэффициент перпендикуляра к ней равен 1, а уравнение этого перпендикуляра , т.е. .

Очевидно, что центр окружности С есть точка пересечения прямой АВ с указанным перпендикуляром, т.е. координаты центра определяются путем решения системы уравнений , . Следовательно, x=2, y=1, т.е. С(2;1). Радиус окружности равен длине отрезка СА, т.е. . Итак, искомое уравнение имеет вид .

Пример 4. Составить уравнение хорды окружности , делящей в точке А(1;2) пополам.

Решение.

Составим уравнение диаметра окружности, проходящего через точку А(1;2). Это уравнение имеет вид . Искомая хорда перпендикулярна диаметру и проходит через точку А, т.е. ее уравнение , или .

Пример 5. Найти уравнение окружности, симметричной с окружностью относительно прямой .

Решение.

Приведем уравнение данной окружности к каноническому виду ; центр окружности находится в точке С(1;2), и ее радиус равен 1.

Найдем координаты центра С₁(x₁;y₁) симметричной окружности, для чего через точку С(1;2) проведем прямую, перпендикулярную прямой ; ее уравнение , где , откуда , или .

Решая совместно уравнения и , получим x=3, y=0, т.е. проекция точки С(1;2) на данную прямую – точка Р(3;0). Координаты же симметричной точки получим по формулам координат средины отрезка: , , таким образом, x₁=5, y₁=-2. Значит, точка С₁(5;-2) – центр симметричной окружности, а уравнение этой окружности имеет вид .

Пример 6. Найти множество середин хорд окружности , проведенных через начало координат.

Решение.

Уравнение множества хорд имеет вид . Выразим координаты точки пересечения хорд с окружностью через k, для чего решим систему уравнений и . Получим квадратное уравнение . Здесь . Но полусумма этих абсцисс дает абсциссу середины хорды, т.е. , а ордината середины хорды . Поэтому два равенства являются параметрическими уравнениями искомого множества точек.

Исключив из этих равенств k (для чего достаточно в соотношении положить ), получим . Таким образом, искомым множеством также является окружность.