23

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Прямая на плоскости

Учебно-методическое пособие по специальности «Химия» 011000.

ВОРОНЕЖ

2005

Утверждено научно-методическим советом математического факультета

28 Февраля 2005 года

Протокол № 6

Составитель Петрова Е.В.

Учебно-методическое пособие подготовлено на кафедре

уравнений в частных производных и теории вероятностей

математического факультета Воронежского

госуниверситета

Рекомендуется для студентов 1 курса дневного отделения

химического факультета

1. Уравнение линии000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

1.1. Уравнение линии как множество точек

Равенство вида

(1)

называется уравнением с двумя переменными x, y, если это равенство справедливо не для всех пар чисел х, у. Примеры уравнений: , , .

Если (1) справедливо для всех пар чисел х, у, то оно называется тождеством. Примеры тождеств: , .

Пусть некоторой линии на плоскости хОу, рассматриваемой как множество точек, соответствует уравнение, связывающее координаты любой точки М (х;у) («текущей точки»), лежащей на этой линии. Такое уравнение называется уравнением данной линии.

Определение. Уравнение (1) называется уравнением линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Из определения следует, что линия L представляет собой множество всех тех точек плоскости (х;у), координаты которых удовлетворяют уравнению (1).

Если (1) является уравнением линии L, то говорят, что уравнение (1) определяет (задает) линию L.

Если в уравнение данной линии подставить координаты любой точки, лежащей на этой линии, то уравнение обращается в тождество. Если же в уравнение линии подставить координаты любой точки, не принадлежащей этой линии, то уравнение не удовлетворяется.

Линия L может определяться и уравнением вида

, (2)

содержащим полярные координаты.

Пример 1. Один конец отрезка перемещается по оси абсцисс, а другой – по оси ординат. Найти уравнение линии, описываемой серединой этого отрезка, если длина отрезка равна с.

Решение.

Пусть М(х,у) – середина отрезка. Длина отрезка ОМ (длин медианы) равна половине гипотенузы, т.е. . С другой стороны, (расстояние точки М от начала координат).

Таким образом, приходим к уравнению

, или .

Это и есть уравнение искомой линии. Геометрически очевидно, что этой линией является окружность радиуса с центром в начале координат.

Пример 2. Составить уравнение линии, расстояние каждой точки которой от точки равно расстоянию этой же точки от прямой .

Решение.

Возьмем на искомой линии произвольную точку М(х;у). Расстояние точки М от точки F определяется по формуле расстояния между двумя точками:

.

Расстояние точки М от прямой найдется из простых геометрических соображений (см. рис.):

.

Так как по условию равенство выполняется для любой точки М, лежащей на искомой линии, то уравнение этой линии можно записать в виде

,

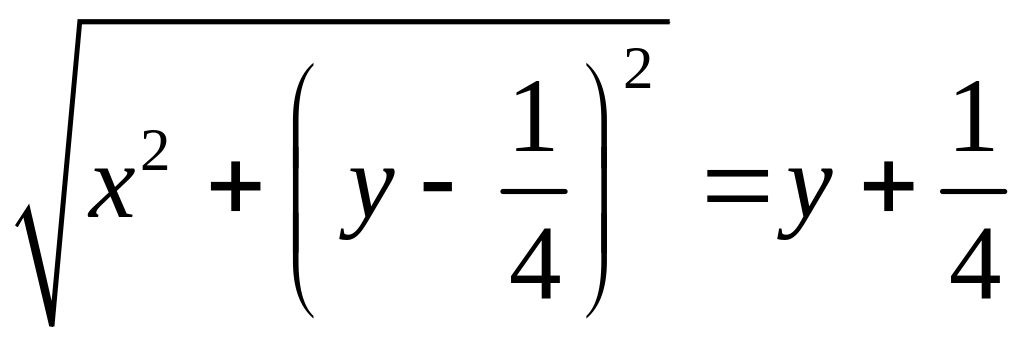или

,

т.е. .

Линия, определяемая уравнение , называется параболой.

Пример 3. Составить уравнение множества точек, произведение расстояний которых от точек и есть постоянная величина, равная .

Решение.

Возьмем на искомой кривой произвольную точку М(х;у). Ее расстояния от точек и составляют , . Из условия задачи следует, что . Таки образом, искомая кривая имеет уравнение

.

Приведем это уравнение к рациональному виду:

,

т.е.

,

или, наконец,

.

Найденная кривая называется лемнискатой.

Пример 4. Составить уравнение лемнискаты в полярных координатах.

Решение.

В уравнении (см. предыдущий пример) переходим к полярным координатам по формулам , . Тогда получим

, или .

Это – уравнение лемнискаты в полярных координатах.

Пример 5. Составить уравнение множества точек, равноудаленных от точек А(1;1) и В(3;3).

Решение.

Пусть точка М принадлежит искомому множеству; тогда . По формуле расстояния между двумя точками находим

,

и уравнение линии может быть записано в виде

.

Возведя обе части последнего равенства в квадрат, получим

,

откуда после приведения подобных членов окончательно приходим к уравнению . Итак, искомым множеством является прямая, которая, как известно, служит серединным перпендикуляром к отрезку АВ.