10.4 Метод декомпозиции на основе агрегирования в задачах большой размерности.

Одной из задач оптимального планирования с большим числом переменных и ограничений является так называемая модель отраслевого планирования. Годовой план области формируется на основе потребностей народного хозяйства в целом в ее продукции. При этом одна часть номенклатуры конечного выпуска фиксируется (так называемый 'госзаказ'), а другая - находится в распоряжении отрасли или концерна. В качестве критерия выбирается максимизация выпуска свободной номенклатуры в заданном ассортиментном соотношении или максимизация прибыли (общая модель). Данная модель приводит к задаче ЛП с блочно-диагональной структурой части ограничений. Связывающие ограничения и критерий оптимальности имеют специфику, обусловленную конкретной моделью планирования. Эта специфика приводит к идее агрегирования переменных при построении декомпозиционного метода решения блочной задачи.

Постановка и математическая модель задачи

Рассмотрим задачу отраслевого планирования. Имеется отрасль (или большой концерн), которая характеризуется множеством заводов , множеством номеров изделий конечной продукции , множеством индексов номенклатуры изделий, производящихся на заводах отрасли , множеством номеров групп оборудования K_j, имеющихся на заводе j, множеством номеров комплектующих изделий, производящихся на заводе .

Предположим, что технологическая цепочка изготовления данного изделия на данном заводе фиксирована. Тогда производственные мощности каждого завода описываются (в рамках модели использования невзаимозаменяемых групп оборудования) следующими ограничениями:

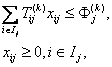(10.4.1)

где x_ij - годовой оборот выпуска изделий типа i на заводе j ; - годовой фонд времени работы оборудования группы k на заводе j ; - затраты времени работы оборудования группы k на заводе j на производство единицы изделия типа i.

Как следует из (10.4.1) величины x_ij определены на каждом заводе j только для . В дальнейшем удобно определить их для всех , полагая для этого x_ij=0 для . Связь между выпуском комплектующих изделий и выпуском конечной продукции описывается соотношением

,                     (10.4.2)

где y_m - годовой выпуск продукции вида m; W_ij - запас изделий вида i на заводе j на начало планового периода; e_im - число изделий вида i, входящих в единицу конечной продукции (вида m); -норматив запаса продукции m, переходящего на следующий год (в относительных единицах).

Предположим сначала, что множество номеров конечной продукции разбито на два непересекающихся подмножества , где

Продукция из подмножества является важнейшей для отрасли с точки зрения народнохозяйственных потребностей, она входит в госзаказ. Объемы выпуска продукции из подмножества либо фиксируются, либо задаются ограничениями снизу,то есть

.                               (10.4.3)

Эта часть номенклатуры конечного выпуска называется обязательной. Предполагается, что существует вектор { } такой, что область допустимых планов не пустая. Продукция из множества  называется свободной, и решение об объемах ее выпуска принимает администрация отрасли (или концерна).

Пусть администрация области определяет вектор свободной номенклатуры

 { }                             (10.4.4)

Вектор { } является недопустимым планом, то есть не существует величин {x_ij}, удовлетворяющих условиям (10.4.1) и (10.4.2). В этом случае возникает проблема сокращения компонент вектора (10.4.4).

Вектор { } является допустимым планом. В этом случае существует бесконечное число способов размещения заказов на изготовление комплектующих изделий по заводам и, кроме того, определенная доля производственных мощностей отрасли может быть не загружена.

Таким образом, в обоих случаях администрация (плановый орган) отрасли сталкивается с необходимостью пересмотра вектора (10.4.4), который можно интерпретировать как желательную структуру выпуска свободной номенклатуры конечной продукции. Тогда конечный план выпуска свободной номенклатуры определяется как:

.

Компоненты вектора  в (10.4.4) называются пропорциями или ассортиментными соотношениями, а величина - числом ассортиментных наборов (числом комплектов).

Далее предположим, что компоненты вектора обязательной номенклатуры фиксированы. Запишем (10.4.2) в соответствии с разбиением вектора конечной продукции

. (10.4.5)

Обозначим суммарный запас изделия в отрасли на начало нового планового периода (года) через , а суммарный объем изделия i, необходимого для выпуска конечной продукции обязательной номенклатуры  и, наконец, і-тую компоненту ассортиментного соотношения выпуска комплектующих изделий обозначим через

.

С использованием этих обозначений (10.4.5) запишется в виде

.

Введем также обозначения

.

Тогда оптимизационная задача запишется окончательно в виде:

                                 максимизировать                                       (10.4.6)

при ограничениях

(10.4.7)

, если  если                                  (10.4.8)

,                     (10.4.9)

.                                   (10.4.10)

Задача (10.4.6)-(10.4.10) является задачей ЛП и для ее решения можно использовать стандартные методы. Однако на практике это связано с трудностями из-за огромной размерности реальных задач отраслевого планирования.

Анализ ограничений этой задачи показывает, что она имеет блочную структуру: ограничения (10.4.7), (10.4.8) относятся к отдельным заводам j и являются блочными, а ограничения (10.4.9) сугубо отраслевые, или связывающие, относятся к всем заводам отрасли. Кроме того, данная блочная задача обладает дополнительно специфическими особенностями : оптимизируемая переменная не входит в блочные ограничения, связывающие ограничения имеют специальный вид, а в критерий входит лишь одна переменная . Эти особенности и учитываются при построении декомпозиционного алгоритма.

Метод разложения на основе агрегирования

Наличие в равенствах (10.4.9) сумм приводит к идее ввести новые переменные - полные выпуски по всем заводам отрасли (концерна):

,                            (10.4.11)

которые естественно назвать агрегированными переменными. Вводятся также удельные выпуски изделия типа i на заводе j:

,

которые еще называют весами (или коэффициентами) агрегирования.

Очевидно, выполняются условия

.     (10.4.12)

Пусть заданы веса агрегирования, удовлетворяющие (10.4.12). Тогда, подставляя в (10.4.6)-(10.4.8) переменные  и вводя обозначения , приходим к задаче в агрегированных переменных:

                                     максимизировать                                        (10.4.13)

при ограничениях

(10.4.14)

;                                (10.4.15)

(10.4.16)

Задачу (10.4.13)-(10.4.16) назовем задачей в агрегированных переменных или макрозадачей.

Запишем двойственную задачу к задаче (10.4.6)-(10.4.8):

                       минимизировать           (10.4.17)

при условиях

;                   (10.4.18)

;                                   (10.4.19)

.                          (10.4.20)

Двойственная задача для задачи в агрегированных переменных записывается так:

                               минимизировать      (10.4.21)

при ограничениях

;                           (10.4.22)

;                                    (10.4.23)

.                          (10.4.24)

Пусть - единственные оптимальные решения задачи (10.4.21)-(10.4.24). Для каждого фиксированного индекса формируются блочные ('заводские') задачи:

                                   максимизировать               (10.4.25)

при ограничениях

,                          (10.4.26)

.                     (10.4.27)

Двойственные задачи для блочных задач (10.4.25)-(10.4.27) при каждом записываются в виде:

                                     минимизировать                (10.4.28)

при ограничениях

.               (10.4.29)

Итеративный процесс решения строется следующим образом [52]. При некоторых фиксированных весовых коэффициентах ,  удовлетворяющих условиям (10.4.12), решается задача в агрегированных переменных (10.4.13)-(10.4.16). Как будет показано в дальнейшем, эта задача при некоторых предположениях решается аналитически. С помощью двойственных оценок  формируют функционалы блочных задач (10.4.25)-(10.4.27). Пусть  - оптимальные решения этих задач. Введем переменные

(10.4.30)

где - оптимальные решения задачи в агрегированных переменных. Величины  называются дезагрегированными решениями. Новые весовые коэффициенты агрегирования определяются в виде функции  от переменных согласно соотношению

(10.4.31)

где .

Заметим, что для коэффициентов , описывающихся (10.4.31), выполняются условия (10.4.12).

Опишем общую схему декомпозиционного алгоритма на основе агрегирования (7,25). Если рассматривать задачи в агрегированных переменных (10.4.13)-(10.4.16) с коэффициентами, удовлетворяющими (10.4.31), то оптимальное значение функционала является функцией от параметров . Эту функцию обозначим через . Возникает задача максимизации функции  на единичном гиперкубе . Пусть максимум достигается при некоторых . Тогда коэффициенты для следующей итерации процесса определяются по формуле (10.4.31) при . Алгоритм формирует последовательность дезагрегированных решений , которые вместе с  являются допустимыми к исходной задаче  (10.4.6)-(10.4.10). Далее проверяется критерий оптимальности решения  для задачи (10.4.6)-(10.4.10) (условие окончания итеративного процесса).Далее доказывается строгая монотонность значений функционала , соответствующих дезагрегированным решениям  и ,и таким образом решается вопрос о сходимости последовательности из допустимых решений  и  к оптимальному решению исходной задачи (10.4.6)-(10.4.10).

Далее предположим, что указанный итеративный процесс начинается с весовых коэффициентов, дающих строго положительное значение  для задачи в агрегированных переменных. А поскольку это число на каждой итерации возрастает, то для всех макрозадач выполняется неравенство > 0. Предположим также, что выпуск каждого изделия ненулевой, то есть , что заведомо выполняется на практике. Сформулируем критерий оптимальности дезагрегированного решения .

Пусть при некоторых коэффициентах , удовлетворяющих (10.4.12), получено оптимальное решение  задачи в агрегированных переменных (10.4.13)-(10.4.16), а  - соответствующее дезагрегированное решение. Пусть - единственное решение двойственной задачи (10.4.21)-(10.4.24). Вводятся обозначения

.                   (10.4.32)

Величины и  представляют собой значения функционалов блочных задач (10.4.25)-(10.4.27) на оптимальном и дезагрегированном решениях соответственно. Положим также

.

Имеет место следующая теорема (52).

Теорема 10.1. Справедливы следующие утверждения:

 а) ;

 б) тогда и только тогда, когда для всех j.

Доказательство. Дезагрегированное решение является допустимым к блочным задачам. Оно удовлетворяет условиям (10.4.17), в силу (10.4.13) и (10.4.16). Это решение удовлетворяет также (10.4.26)  согласно следующей цепочке неравенств:

(10.4.33)

Поскольку  допустимые решения исходных ('заводских') задач (10.4.25)-(10.4.27), а - их оптимальные решения, то утверждение а) теоремы 10.1 - доказано. Далее в силу определений  и  и утверждения а) теоремы, устанавливаем справедливость утверждения б) теоремы. Следовательно, теорема доказана.

Следующая теорема устанавливает условие оптимальности дезагрегированного решения (52).

Теорема 10.2. Пусть для оптимальных решений ,  и  прямой и двойственной макрозадач и оптимальных решений блочных задач { } выполняются равенства

.                            (10.4.34)

Тогда дезагрегированное решение , где , , составляет оптимальный план исходной задачи (10.4.6)-(10.4.10).

Доказательство. Поскольку > 0, то в силу теоремы 2.7 двойственности условие (10.4.23) выполняется как строгое равенство, то есть . Умножая равенства (10.4.15), выписанные для оптимального решения, на и суммируя по i, получаем

.

Из последних двух соотношений имеем

Рассмотрим дезагрегированое решение . Легко убедиться , что это решение будет допустимо к исходной задаче (10.4.6)-(10.4.10), а значение целевого функционала на этом решении есть .Имеем следующую цепочку равенств:

.

Сравнивая последнее равенство с (10.4.34), получаем

.                        (10.4.35)

Далее рассмотрим оптимальные решения ,  двойственных блочных задач (10.4.28)-(10.4.30). Можно легко проверить, что набор { }, { }, , , является допустимым планом к двойственной задаче (10.4.27)-(10.4.30). Функционал на этом решении принимает значение

.                     (10.4.36)

По теореме 2.2 двойственности (см.гл.2) для блочных задач имеют место равенства

, .                   (10.4.37)

Подставляя (10.4.37) в (10.4.36), получаем

(10.4.38)

Итак, имеем допустимые решения пары двойственных задач (10.4.6)-(10.4.10) и (10.4.17)-(10.4.20), значения целевых функций которых выражаются соответственно через (10.4.35) и (10.4.38).

Равенство

,                                 (10.4.39)

согласно основной теореме двойственности 2.2, обеспечивает оптимальность решений  для исходной задачи (10.4.6)-(10.4.10). Но из (10.4.35) и (10.4.38) следует, что равенство (10.4.39) эквивалентно , или, в силу леммы, . Следовательно, теорема 10.2 доказана. Таким образом, выполнение соотношения (10.4.33) является условием окончания алгоритма.

Аналогично доказывается и следующая теорема [52].

Теорема 10.3. Пусть исходная задача (10.4.6)-(10.4.10) имеет решения и при некоторых  получен дезагрегированный план  , не оптимальный для задачи (10.4.6)-(10.4.10). Тогда существуют такие j, для которых и потому имеет место неравенство

.                                (10.4.40)