Декомпозиция на основе агрегировання для общей модели отраслевого планирования.

Выше была рассмотрена модель отраслевого планирования с критерием максимума выпуска свободной части конечной продукции. Соответствующая целевая функция зависит от переменной .

Рассмотрим теперь общий случай задачи отраслевого планирования. Пусть  - стоимость единицы продукции x_ij. Пусть, кроме того, при выпуске изделий і-го вида на заводе j используются некоторые виды общих ресурсов l, , которые находятся в распоряжении отрасли (концерна), и их общие объемы ограничены. Обозначим через b_ijl расход ресурса l - го вида на выпуск продукции і-го вида (x_i) на заводе j, а P_l - реальный объем этого ресурса в отрасли, P_jk - объем собственного к-го ресурса на заводе j, b_ijk - норма расхода  к-го ресурса на производство продукции i-го вида.

Тогда рассмотрим задачу максимизации прибыли от реализации продукции при ограничениях на общие ресурсы. Соответствующая модель задачи имеет вид:

                                    максимизировать                     (10.4.55)

при ограничениях

(10.4.56)

, при , x_ij=0 при                                         (10.4.57)

, .                         (10.4.58)

Здесь соотношения (10.4.56), (10.4.57) - блочные, где номер j, как и ранее, соответствует фиксированному блоку, а (10.4.58) - связывающие ограничения.

Для задачи (10.4.55)-(10.4.58) запишем двойственную задачу:

                    минимизировать        (10.4.59)

при ограничениях

(10.4.60)

;;;;,                  (10.4.61)

причем, переменные  соответствуют (10.4.56), а _l - ограничениям (10.4.58).

Как и ранее, введем агрегированные переменные ; , и весовые коэффициенты агрегирования , Фиксируя коэффициенты  и подставляя  в (10.4.55) - (10.4.58) получим задачу в агрегированных переменных:

                                      максимизировать                 (10.4.61)

при ограничениях

;                    (10.4.62)

(10.4.63)

; .                             (10.4.64)

Здесь введены обозначения

(10.4.65)

Двойственная задача для задачи (10.4.61)-(10.4.64) имеет вид:

                    минимизировать            (10.4.66)

при ограничениях

;              (10.4.67)

; ;;;,              (10.4.68)

где переменные соответствуют (10.4.62), а переменные - (10.4.63).

Пусть { } - оптимальные двойственные оценки (переменные) задачи (10.4.66)-(10.4.68). Сформулируем задачи для отдельных блоков:

\                   минимизировать           (10.4.69)

при ограничениях

; ;                          (10.4.70)

при , x_ij=0 при  .            (10.4.71)

Двойственные задачи для блочных задач имеют вид:

                        минимизировать                     (10.4.72)

при ограничениях

,                     (10.4.73)

;                               (10.4.74)

где двойственные переменные соответствуют (10.4.70).

Алгоритм решения задачи конструируется по общей схеме алгоритма декомпозиции на основе агрегирования. При этом сводим задачу (10.4.55)-(10.4.58) к задачам меньших размерностей. Действительно, исходная задача имеет  переменных. Задача в агрегированных переменных (10.4.61) содержит I переменных, а блочной задачи имеют каждая по I_j переменных, наконец, задача максимизации функции  на единичном гиперкубе включает J переменных.

На каждом шаге итеративного процесса неоднократно решается задача в агрегированных переменных (10.4.61), которая имеет небольшое количество переменных X_i,  и большое число ограничений.

Сформулируем признак оптимальности промежуточного дезагрегированного решения. Пусть при некоторых весовых коэффициентах получено оптимальное решение  макрозадачи (10.4.61)-(10.4.61), а  - соответствующее дезагрегированное решение. Пусть - единственное оптимальное решение задачи (10.4.66)-(10.4.68), а - оптимальные решения блочных задач (10.4.69)-(10.4.71).

Теорема 10.7. Достаточным условием оптимальности решения {} задачи (10.4.55)-(10.4.58) является выполнение равенства

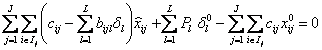.    (10.4.75)

Если же задача (10.4.55)-(10.4.58) - разрешима и { } - неоптимальное решение, то в соотношении (10.4.75) знак равенства заменяется знаком '>'.

Доказательство. Дезагрегированное решение  является допустимым к исходной задаче (10.4.55)-(10.4.58). Это проверяется непосредственной подстановкой  в (10.4.56) и (10.4.58) с учетом (10.4.62), (10.4.63) и обозначений (10.4.11). Соответствующее значение целевой функции исходной задачи равно

,                                  (10.4.76)

Набор { , },где , , , - оптимальные решения задач, двойственных к блочным (10.4.72), является допустимым решением задачи, двойственной для задачи (10.4.55)-(10.4.58). Это следует из соотношений (10.4.73), (10.4.74), (10.4.60).

Значение функционала для указанного решения есть

.                       (10.4.76)

Согласно теореме 2.5 двойственности равенство =f ⁰ обеспечивает оптимальность допустимого решения { } для задачи (10.4.55)-(10.4.58). Если же решение { } неоптимально для задачи (10.4.55)-(10.4.58) при условии ее разрешимости, то >f ⁰ .

Поскольку набор  - оптимальные решения задач, двойственных к блочным (10.4.72), то по теореме 2.5, для оптимальных решений блочных задач и двойственных к ним будем иметь

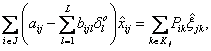для всех .

Подставляя это выражение в (10.4.76), с учетом , получим условия оптимальности (10.4.75).

Таким образом, теорема 10.7 доказана.

Подытоживая, получим критерий оптимальности в виде

(10.4.77)

Опишем теперь алгоритм декомпозиции на основе агрегирования для задачи ЛП. Пусть общая задача ЛП с блочно-диагональной структурой части ограничений задана в виде (10.4.55)-(10.4.58).

Предварительный этап.

Задаемся начальными коэффициентами агрегирования ( ), решаем задачу в агрегированных переменных (10.4.61)-(10.4.64) и находим , , .

Решаем двойственную задачу (10.4.66)-(10.4.68) и находим оптимальные двойственные переменные { },{ }.

Решаем блочные задачи (10.4.69)-(10.4.71) и находим оптимальные решения { }.

Проверяем условие (10.4.77). Если оно строго равно нулю, то конец, - оптимальное решение, в противном случае, если оно имеет знак >, переходим к первой итерации.

(k+1)-я итерация. Пусть в результате k-й итерации получены (k) и (k).

Записываем

.

Находим

и определяем                  и .

В случае, если принять = для всех j, можно использовать для поиска эффективный метод одномерного поиска, например Фибоначчи, или 'золотого сечения'.

Решаем задачу в агрегированных переменных (10.4.61)-(10.4.64) при заданных  и находим (k+1); ; ( k+1).

Решаем двойственную задачу (10.4.66)-(10.4.68) к агрегированной и находим оптимальные оценки { }, .

Решаем блочные задачи (10.4.69)-(10.4.71) при найденных значениях { },  и находим { }; ; .

Проверяем признак оптимальности. Если при найденных значениях { },{ } и { } условие (10.4.75) выполняется как строгое равенство, то конец { } - оптимальные решения исходной задачи, в противном случае переходим к (k+1)-й итерации.

Пример 10.5. Решить методом агрегирования следующую задачу ЛП:

                                         максимизировать (x₁₁+2x₁₂+3x₁₃+2x₂₁+3x₂₂+x₂₃)                            (1)

при ограничениях

(2)

Первая итерация.

Выбираем начальные коэффициенты агрегирования

Составляем задачу в агрегированных переменных:

max 1,8x₁+0,66x₂                                                         (3)

при ограничениях

(4)

Решаем ее графически (см.рис.10.2) и находим х(1)=8,4 ; х(2)=5 ; max f(x₁,x₂)=18,42. Одновременно находим и дезагрегированное решение:

Записываем задачу, двойственную к агрегированной:

(5)

при ограничениях

(6)

.

Для ее нахождения заметим, что в оптимальном решении прямой задачи как строгие равенства выполняются ограничения а) и ж). Это означает, что в оптимальном решении двойственной задачи соответствующие им двойственные переменные  и  не равны нулю. Тогда, решая систему ограничений (6) относительно уравнений

, находим

При этом  min =18,42.

Записываем подзадачи для отдельных блоков.

Первая подзадача (І=1): найти

(7)

при ограничениях

Решив ее графически, находим

Вторая подзадача (І=2): найти

(8)

при ограничениях

Находим ее решение :

Третья подзадача: найти

при ограничениях

Решив ее (например графически), находим

Проверяем условие оптимальности:

Поскольку , то текущее решение не оптимально, и переходим ко второй итерации.

Следующие итерации выполняем аналогично - через три итерации получим решение { }, для которого выполняется признак оптимальности:

Поскольку (3)=0, то дезагрегированное решение { (3)} - оптимально. Оно равно:

Для этого решения f({ })=28.