3.2 Лабораторная работа «Нахождение кратчайшего пути»

Цель работы. Выработать у студентов практические навыки использования функций пакета networks для решения задач на нахождение кратчайшего пути.

Задание. В приведенной таблице заданы веса дуг, соединяющих узлы V_1, V_2, V_3, V_4, V_5, V_6, V_7, V₈ некоторой сети. Прочерк в клетке таблицы означает, что два узла не являются смежными. Определите кратчайшие пути, соединяющие узел V₁ с остальными узлами сети и их длины. ₋ номер варианта.

	V1	V2	V3	V4	V5	V6	V7	V8
V1	-	10	20	15	-	-	-	-
V2	-	-		-		8	10	-
V3	-	-	-	4	-	5	-	-
V4	-	-	-	-	-		-	-
V5	-	-	-	-	-	1	12	-
V6	-	-	-	-	-	-	15	5
V7	-	-	-	-	-	-	-	1
V8	-	-	-	-	-	-	-	-

Пример выполнения работы

Задача. Дана сеть (рис. 1), дуги которой помечены числами, равными их длинам. Требуется найти кратчайшие пути, ведущие от узла 1 к каждому из остальных узлов сети.

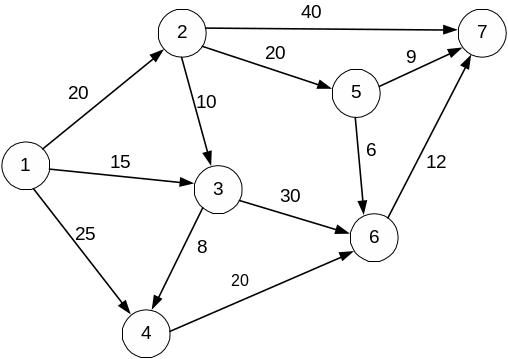
Рисунок 1

Решение. Задача нахождения кратчайшего пути в графе в Maple решается с помощью алгоритма Дейкстры (см. [6], стр. 219). Опишем сеть, изображенную на рисунке 1. Загрузим пакет и зададим граф, содержащий семь изолированных узлов (не соединенных ребрами). Обозначим его идентификатором .

> with(networks):

> G:=void(7):

Зададим списки дуг и соответствующих им весов . В качестве замечания отметим, что в ориентированном графе дуга окаймляется квадратными скобками – [1,2], а в неориентированном графе ребро окаймляется фигурными – {1,2}.

>E:=[[1,2],[1,3],[1,4],[2,3],[2,5],[2,7],[3,4],[3,6],[4,6],[5,6],[5,7]];

Результат на экране:

> W:=[20,25,15,10,20,40,8,30,20,6,9,12];

Результат на экране:

Получим сеть, добавив в граф списки дуг и соответствующих им весов:

> addedge(E,weights=W,G);

Получим на экране

В виде замечания отметим, что здесь использован один из нескольких способов задания графов в среде Maple (см., например, [2]).

Определим дерево кратчайших путей сети с помощью функции shortpathtree. Обозначим его идентификатором .

> T:=shortpathtree(G,1):

Нарисуем дерево :

> draw(T);

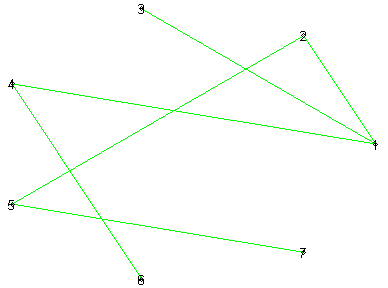
Из выведенного на экран графического объекта мы можем определить, через какие узлы сети пролегают кратчайшие пути, ведущие от узла 1 к каждому из остальных узлов сети. То же самое можно сделать с помощью функции path. Определим пути, ведущие от узла 1 к остальным узлам дерева . Чтобы не повторять однотипную операцию несколько раз, организуем цикл с помощью функции seq:

> seq(path([1,i],T),i=2..7);

На экране получим результат

Найдем расстояния от узла 1 до каждого из узлов 2, 3, 4, 5, 6, 7 дерева с помощью функции vweight.

> vweight(T);

Результат выполнения – таблица, из которой видно, что вершине 1 присвоена метка (вес) 0, вершине 2 – метка 20, следовательно, длина кратчайшего маршрута от узла 1 к узлу 2 равна 20. Аналогично имеем: длина кратчайшего маршрута от узла 1 к узлу 3 равна 25, от узла 1 к узлу 4 – 15, от узла 1 к узлу 5 – 40, от узла 1 к узлу 6 – 35, от узла 1 к узлу 7 – 49: