§ 4. Зведення загального рівняння другого порядку до канонічного вигляду.

1. Перетворення декартової системи координат на площині. Нехай на площині задано два базиси та , які визначають дві декартові системи координат та відповідно. Нехай змінна точка площини має координати та в системах координат та відповідно. Позначимо через радіус-вектор точки , так що

. (34)

Розкладемо кожний з векторів базису за векторами базису

(35)

і підставимо отримані розклади в рівність (34):

.

Звідси,

(36)

Рівності (35) називаються формулами переходу до іншого базису, а рівності (36) – формулами переходу до іншої системи координат.

2. Поворот системи координат. Розглянемо окремий випадок перетворення декартової системи координат, який полягає у повороті на деякий кут прямокутної декартової системи координат .

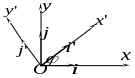Нехай прямокутна декартова система координат з базисом отримується поворотом на кут прямокутної декартової системи координат з базисом . Оскільки координатами одиничного вектора є його напрямнні косинуси, то

.

Тоді формули (35), (36) набувають вигляду

(35′)

(36′)

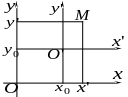
3. Паралельне перенесення системи координат. Нехай система координат отримується перенесенням системи координат так, що початок координат переходить в точку , яка має координати в системі координат , а осі координат , паралельні до осей , відповідно. Тоді, з рисунка, для змінної точки , яка має координати в системі та координати в системі , справджуються рівності

(37)

Формули (37) називаються формулами паралельного перенесення системи координат.

4. Класифікація кривих другого порядку. Кривою другого порядку називається лінія на площині координати кожної точки якої в деякій прямокутній декартовій системі координат задовольняють рівняння

. (38)

Рівняння (38) називається загальним рівнянням кривої другого порядку.

Позначимо . Крива другого порядку називається кривою гіперболічного типу, якщо ; якщо , то крива називається кривою параболічного типу; у випадку крива називається кривою еліптичного типу.

5. Спрощення загального рівняння рівняння поворотом системи координат. Рівнянню (38) завжди можна надати вигляду

(39)

в системі координат , яка отримується поворотом системи координат на певний кут. Справді, підставимо в рівняння (38) замість їх значення з рівностей (36′):

.

Знайдемо половину коефіцієнта при добутку :

,

або

.

Виберемо кут так, щоб . Тоді

.

Якщо , то і звідси , або .

Якщо ж , то , тобто .

6. Спрощення рівняння паралельним перенесенням системи координат. Якщо в рівняння (39) входить квадрат однієї з координат з ненульовим коефіцієнтом, то за допомогою паралельного перенесення системи координат вздовж відповідної осі можна добитися, щоб коефіцієнт при першому степені цієї координати перетворився в нуль. Справді, нехай . Тоді в рівнянні (39) можна виділити повний квадрат при коефіцієнті :

.

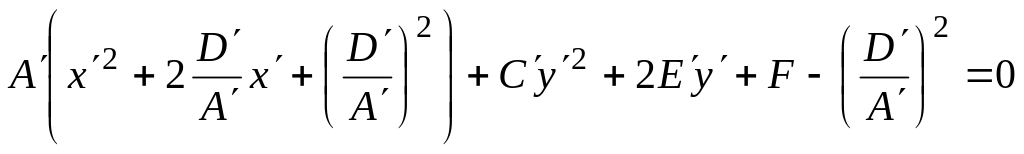Виконаємо паралельне перенесення системи координат за формулами

Рівняння кривої набуде вигляду

,

де .

7. Криві еліптичного типу. Нехай для рівняння (38) , тобто рівняння (38) задає криву еліптичного типу. Зрозуміло, що поворот на кут системи координат не змінює самої кривої, тобто не змінює її типу. Звідси, для рівняння кривої (39) , тому , і коефіцієнти мають однакові знаки. Двократним застосуванням перетворень п.6, один раз відносно координати , а другий раз відносно , рівнянню (39) можна надати вигляду

. (40)

Якщо і знак не збігається зі знаком та , то рівнянню (40) можна надати вигляду

,

де , , тобто рівняння (38) задає еліпс.

Якщо і знак збігається зі знаком та , то рівняння (40) зводиться до рівняння уявного еліпса

, , ,

яке не визначає жодної дійсної точки.

Якщо ж , то з рівняння (40) отримуємо рівняння пари уявних прямих

, , ,

яке визначає одну дійсну точку.

8. Криві гіперболічного типу. Нехай тепер для кривої (38) , що рівносильно тому, що для тої самої кривої, заданої рівнянням (39), . Звідси, , і та мають супротивні знаки. Як і в попередньому пункті, двократним застосуванням паралельного перенесення системи координат вздовж осей та рівнянню (39) можна надати вигляду (40).

Якщо , то можна вважати, що знак збігається зі знаком коефіцієнта . Тоді з рівняння (40) отримуємо канонічне рівняння гіперболи

,

де , .

Якщо ж , то рівняння (40) має вигляд

, , ,

і визначає пару прямих та , які перетинаються.

9. Криві параболічного типу. Нехай тепер рівняння (38) задає криву параболічного типу, тобто . Для рівняння (39) тої самої кривої . Тоді або , або . Не зменшуючи загальності, можна вважати, що , . Тоді паралельним перенесенням системи координат вздовж осі рівняння (39) зводиться до рівняння

. (41)

Нехай . Тоді останньому рівнянню можна надати вигляду

.

Виконавши паралельне перенесення системи координат

дістаємо

, .

Це канонічне рівняння параболи.

Якщо ж , то рівняння (41) має вигляд

. (42)

Нехай і коефіцієнти та мають різні знаки. Тоді рівняння (42) має вигляд

, ,

і визначає пару паралельних прямих та .

Якщо ж і коефіцієнти , мають однакові знаки, то рівняння (42) має вигляд

,

яке визначає пару уявних паралельних прямих.

Якщо , то рівняння (42) збігається з рівнянням , яке задає пару прямих, що збіглися.