Розділ 4. Криві та поверхні другого порядку

§ 1. Еліпс

1. Канонічне рівняння еліпса. Еліпсом називається лінія на площині сума відстаней від кожної точки якої до двох фіксованих точок, які називаються фокусами, є величина стала і дорівнює .

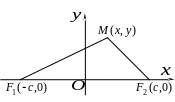Виберемо прямокутну декартову систему координат так, щоб фокуси , еліпса були розташовані на осі абсцис симетрично відносно початку координат і нехай вони мають відповідно координати та . Розглянемо довільну точку еліпса і знайдемо рівняння еліпса. Згідно з означенням еліпса,

. (1)

Зрозуміло, що еліпс існує лише при умові, що , тобто

. (2)

Очевидно,

, .

Підставивши значення та в (1), дістанемо

,

або

.

Піднесемо обидві частини рівності до квадрата:

.

Після зведення подібних членів маємо

.

Піднесемо ще раз до квадрата

.

Звідси,

.

Оскільки , то можна позначити

, (3)

і рівність набуває вигляду

.

Поділивши обидві частини на дістаємо канонічне рівняння еліпса

. (4)

Зауваження. При рівняння еліпса (4) перетворюється в рівняння кола радіуса з центром у початку координат.

2. Форма еліпса. З (4) , , тобто , , звідки , . Це означає, що еліпс цілком лежить у прямокутнику , .

Якщо точка лежить на еліпсі, тобто її координати задовольняють рівняння (4), то координати точки також задовольняють рівняння еліпса (4), тому точка також лежить на еліпсі. Таким чином, еліпс є лінією, симетричною відносно осі ординат. Точно так само можна побачити, що еліпс симетричний відносно осі абсцис і відносно початку координат. Отже, еліпс має дві взаємно перпендикулярні осі симетрії, які називаються головними осями еліпса. Точка перетину головних осей – центр симетрії еліпса – називається центром еліпса.

Точки перетину еліпса з головними осями називаються вершинами еліпса. Оскільки головними осями є осі координат, то вершини еліпса лежать на осях координат і знайти їх можна з рівняння (4). Покладемо в (4) . Тоді , тобто еліпс перетинається з віссю абсцис у точках та , які є вершинами еліпса. Точно так само знаходимо, що еліпс перетинається з віссю ординат у вершинах та . Відрізок називається великою віссю, а – малою віссю. Відрізки , називаються великими півосями, а , – малими півосями. Довжина відрізка , яка дорівнює , називається фокусною відстанню.

Завдяки тому, що еліпс симетричний відносно осей координат, досить розглянути форму еліпса у першій чверті. Для цього розв’яжемо рівняння (4) відносно :

.

При , тобто маємо вершину ; якщо зростає від нуля до , то спадає від до нуля. Отже, еліпс має такий вигляд

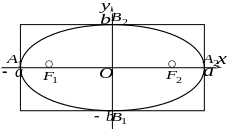
3. Ексцентриситет еліпса. Ексцентриситетом еліпса називається величина

. (5)

Оскільки , то . При . Звідси, завдяки (3), дістаємо, що , тобто еліпс переходить у коло. Якщо ж , то , тому , тобто еліпс сплющується до відрізка . Таким чином, ексцентриситет характеризує ступінь сплющеності еліпса.

Покажемо, що еліпс можна отримати рівномірним стиском кола. Нехай коло радіуса задано рівнянням , або

. (6)

Виконаємо рівномірний стиск площини вздовж осі в разів. Тоді точка кола п ерейде в точку , , , а коло (6) перейде в лінію

.

Звідси, позначивши через , отримуємо рівняння еліпса

.

.

4. Фокальні радіуси еліпса. Для кожної точки еліпса відрізки та називаються її фокальними радіусами. Позначимо через довжину відрізка , а через – довжину відрізка . Знайдемо і .

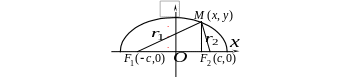
З рисунка

.

Звідси,

. (7)

.

Остаточно,

. (8)

5. Директриси еліпса. Дві прямі, перпендикулярні до великої осі еліпса і віддалені від центра еліпса на відстань , називаються директрисами еліпса.

Згідно з означенням, директриси еліпса визначаються рівняннями

. (9)

Оскільки , то , тобто директриси не перетинають еліпса. Фокус і директриса еліпса, розташовані по один бік від малої осі еліпса, будемо називати відповідними, так що для фокуса відповідною є директриса , а для фокуса – директриса .

Наступна властивість директрис є характеристичною властивістю еліпса.

Теорема. Точка лежить на еліпсі тоді і лише тоді, коли відношення відстані цієї точки від фокуса до відстані від відповідної директриси є величина стала і дорівнює ексцентриситету еліпса.

Доведення. Нехай точка лежить на еліпсі

. (10)

Т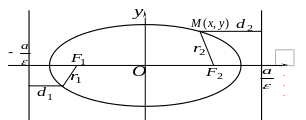 оді відстань від точки до фокуса обчислюється за формулою , а відстань від точки до відповідної директриси – за формулою . Звідси,

.

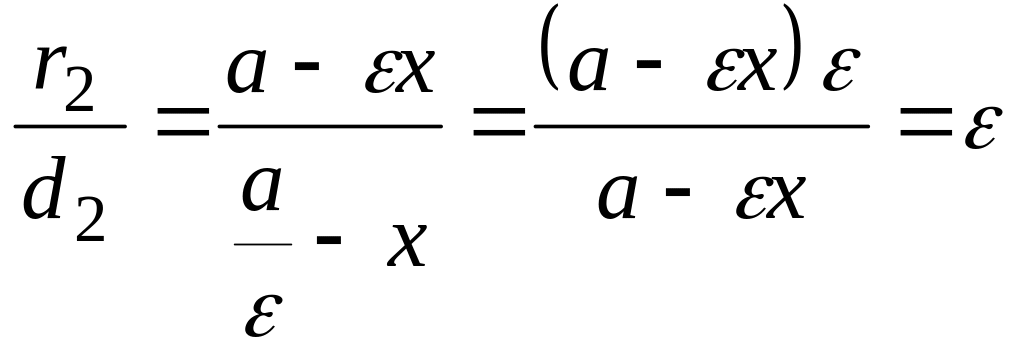Точно так само

.

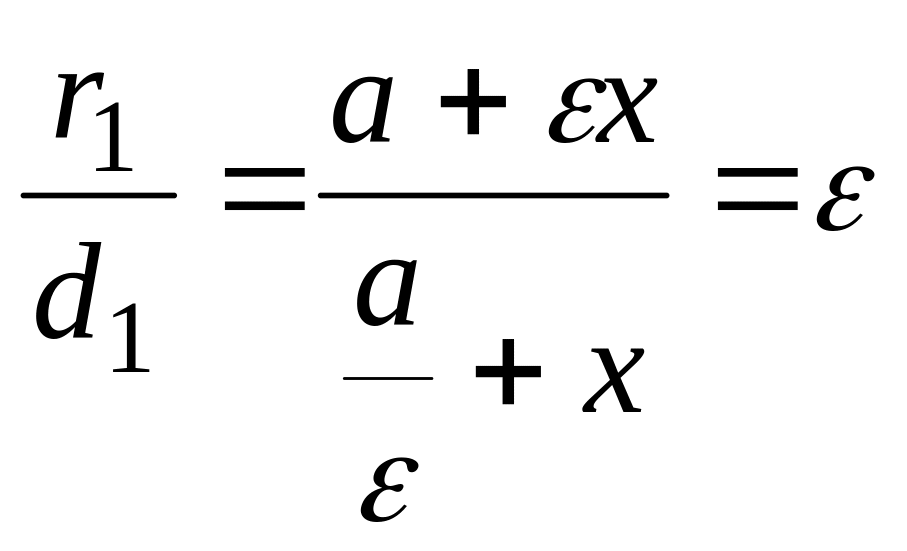Навпаки, нехай – деяка точка площини, для якої , де – відстань від точки до фокуса еліпса (10), а – відстань від точки до відповідної директриси того самого еліпса. Покажемо, що точка лежить на еліпсі (10). Справді, як відстань між двома точками. З нормального рівняння директриси дістаємо, що відстань від точки до цієї директриси дорівнює . Тоді

,

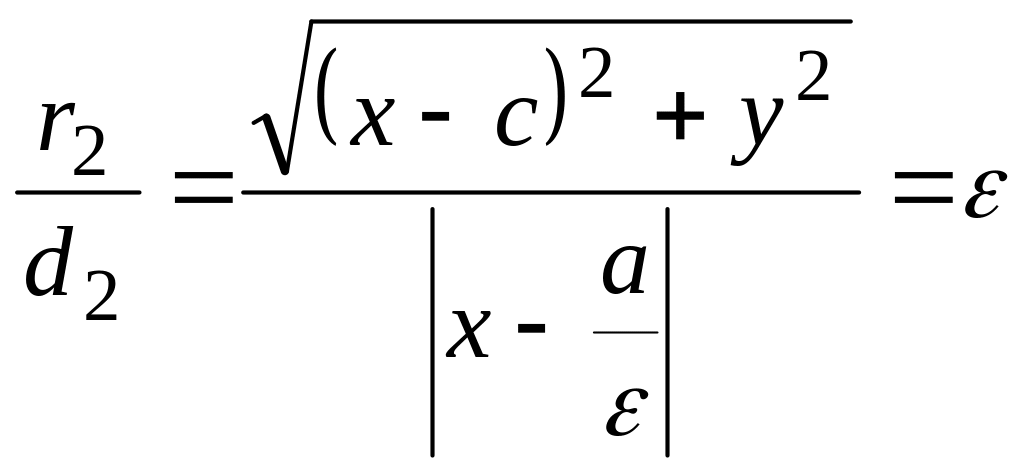або

.

Звідси, після піднесення обидвох частин рівності до квадрата,

або

.

Після зведення подібних членів рівність набуває вигляду

,

а після послідовних замін та – такого:

.

Поділивши обидві частини цієї рівності на , остаточно дістаємо

,

тобто координати точки задовольняють рівняння еліпса (10).

6. Дотична до еліпса. Знайдемо рівняння дотичної до еліпса в точці . Для цього використаємо рівняння прямої з кутовим коефіцієнтом, що проходить через задану точку

. (11)

Кутовий коефіцієнт дотичної до еліпса в точці дорівнює . Знайдемо диференціюванням рівняння (10) еліпса:

,

звідки

.

Зокрема,

.

Підставимо в (11) замість його значення :

.

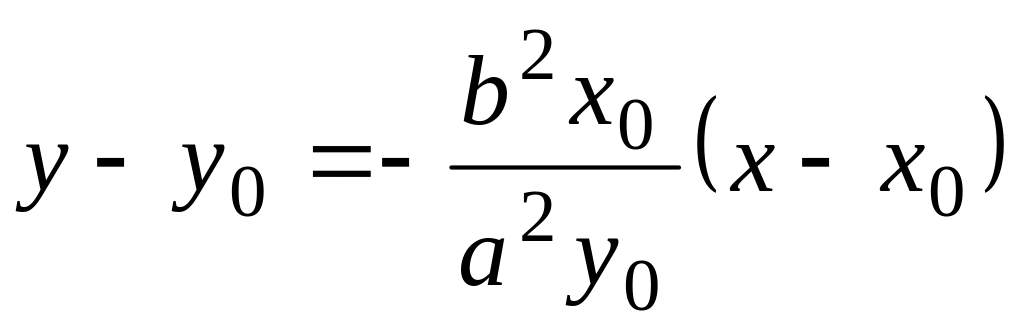Звідси,

.

Поділивши обидві частини на , дістанемо

.

Враховуючи, що координати точки задовольняють рівняння еліпса, тобто

,

остаточно дістаємо рівняння дотичної до еліпса в точці :

. (12)