§ 2. Гіпербола

1. Канонічне рівняння гіперболи. Гіперболою називається лінія на площині для кожної точки якої модуль різниці відстаней до двох фіксованих точок, які називаються фокусами, є величина стала і дорівнює .

Розташуємо фокуси та на осі абсцис прямокутної декартової системи координат симетрично відносно початку координат і позначимо відстань між ними через . Тоді фокуси і мають координати та відповідно. Нехай – довільна точка гіперболи. За означенням гіперболи

. (13)

Оскільки в трикутнику різниця двох сторін менша від третьої сторони , то для гіперболи , або . Знайдемо та як відстані між двома точками

,

і підставимо в рівність (13):

.

Звідси,

,

або

.

Піднесемо обидві частини рівності до квадрата:

.

Після зведення подібних членів маємо

.

Підносимо ще раз до квадрата:

і зводимо подібні члени

.

Оскільки для гіперболи , то , тому можна позначити

. (14)

Тоді попередня рівність набуває вигляду

.

Поділивши обидві частини на , дістаємо канонічне рівняння гіперболи

. (15)

2. Симетрія та вершини гіперболи. Рівняння (15) містить лише квадрати змінних координат та . Тому, якщо координати точки задовольняють рівняння (15), то це рівняння задовольняють і координати точок , , . Точки , симетричні до точки відносно осі ординат та осі абсцис відповідно, а точка – відносно початку координат. Звідси, гіпербола є симетричною лінією відносно осей координат та початку координат. Отже, гіпербола має дві взаємно перпендикулярні осі симетрії, які називаються головними осями гіперболи. Точка перетину головних осей є центром симетрії гіперболи і називається її центром.

Точки перетину гіперболи з головними осями називаються вершинами гіперболи. Для гіперболи, заданої канонічним рівнянням, головними осями є осі координат, тому вершини гіперболи лежать на осях координат. Поклавши в рівнянні (15) , знайдемо абсциси точок перетину гіперболи з віссю : , звідки . Таким чином, вершинами гіперболи є точки та . Якщо в рівнянні (15) покласти , то отримаємо рівняння

,

яке не має дійсних розв’язків, тобто гіпербола не перетинається з віссю .

Вісь симетрії, яка перетинає гіперболу, називається дійсною віссю симетрії, а вісь симетрії, яка не перетинає гіперболи, називається уявною віссю симетрії, так що для гіперболи (15) вісь є дійсною віссю, а вісь – уявною віссю симетрії. Відрізок довжиною називається дійсною віссю гіперболи, а відрізок, який сполучає точки , називається уявною віссю гіперболи.

Фокуси , гіперболи розташовані на її дійсній осі. Довжина відрізка називається фокусною відстанню.

3. Асимптоти гіперболи. Завдяки симетрії гіперболи можна обмежитись дослідженням лише тої її частини, яка лежить у першій чверті і визначається рівнянням

. (16)

Розглянемо пряму

. (17)

Зведемо її рівняння до нормального вигляду

(18)

і знайдемо відстань від змінної точки лінії (16), до прямої (17). Зазначимо, що якщо точка лежить на лінії (16), то вона має координати . Підставивши координати точки в ліву частину рівняння (18), знайдемо

.

Звідси, при . Це означає, що при необмеженому зростанні частина гіперболи (16) необмежено наближується до прямої (17).

Зауважимо, що пряма

(19)

симетрична до прямої (17) відносно осей координат. Оскільки гіпербола також симетрична відносно осей координат, то пряма (19) має аналогічну до прямої (17) властивість.

Прямі

називаються асимптотами гіперболи.

4. Форма гіперболи. З рівняння гіперболи дістаємо, що , або , тобто і . Звідси, всі точки гіперболи лежать справа від прямої і зліва від прямої , тобто гіпербола складається з двох ізольованих частин. Та її частина, для точок якої , називається правою віткою гіперболи, а та частина, для точок якої , називається лівою віткою гіперболи.

Для побудови гіперболи зручно спочатку побудувати її асимптоти, а потім будувати саму гіперболу.

5. Ексцентриситет гіперболи. Ексцентриситетом гіперболи називається величина

. (20)

Оскільки для гіперболи , то .

6. Фокальні радіуси. Для точок правої вітки гіперболи

.

Звідси,

. (21)

Точно так само

. (22)

Вправа. Показати, що для точок лівої вітки гіперболи

, (23)

. (24)

7. Директриси гіперболи. Дві прямі, перпендикулярні до дійсної осі гіперболи і віддалені від центра гіперболи на відстань , називаються директрисами гіперболи.

За означенням, директриси гіперболи мають рівняння

. (25)

Директриси не перетинають гіперболи, бо . Фокус і директриса гіперболи, розташовані по один бік від уявної осі, називаються відповідними.

Директриси мають таку характеристичну властивість.

Теорема. Точка належить гіперболі тоді і лише тоді, коли відношення відстані цієї точки від фокуса до відстані від відповідної директриси є величина стала і дорівнює ексцентриситету гіперболи.

Доведення. Справді, нехай точка належить правій вітці гіперболи

. (26)

Т оді для фокуса , , а для відповідної йому директриси , , тому

.

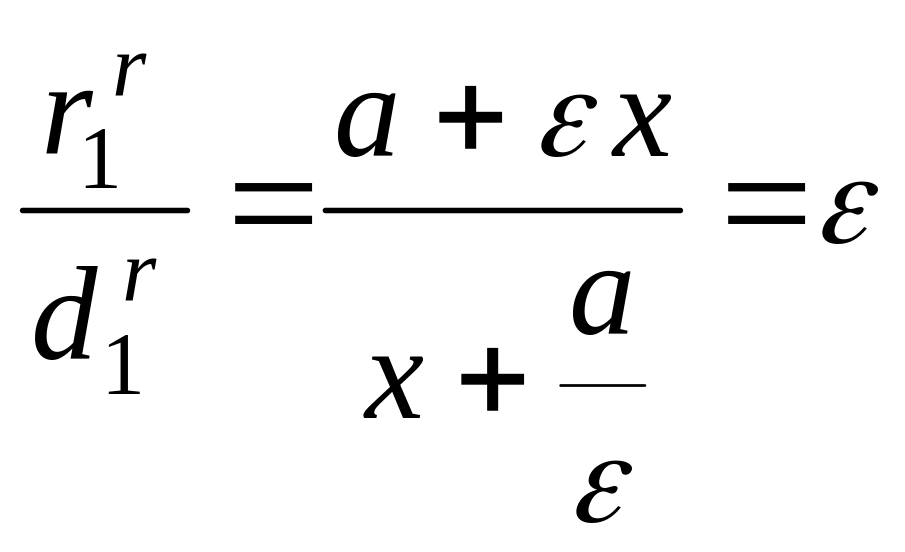Для фокуса , , а для відповідної йому директриси , , звідки

.

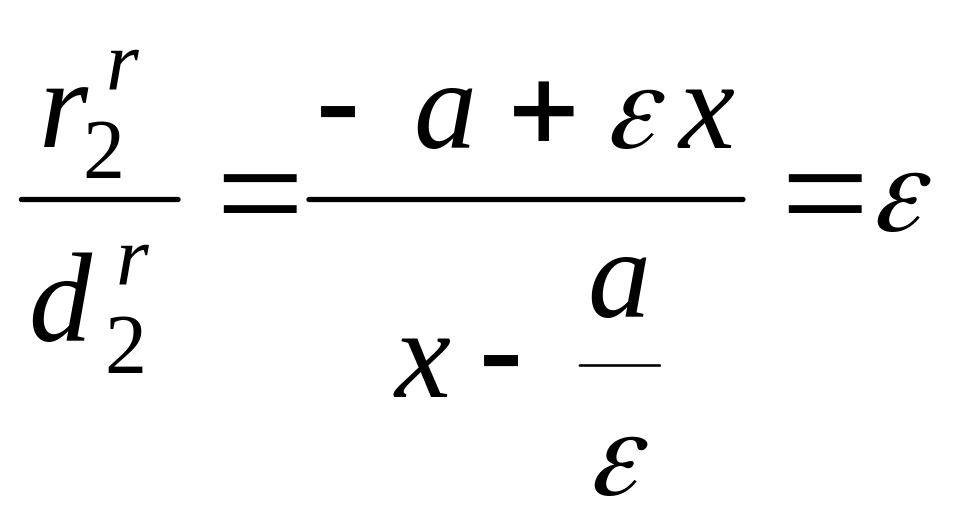Вправа. Довести, що якщо точка належить лівій вітці гіперболи, то .

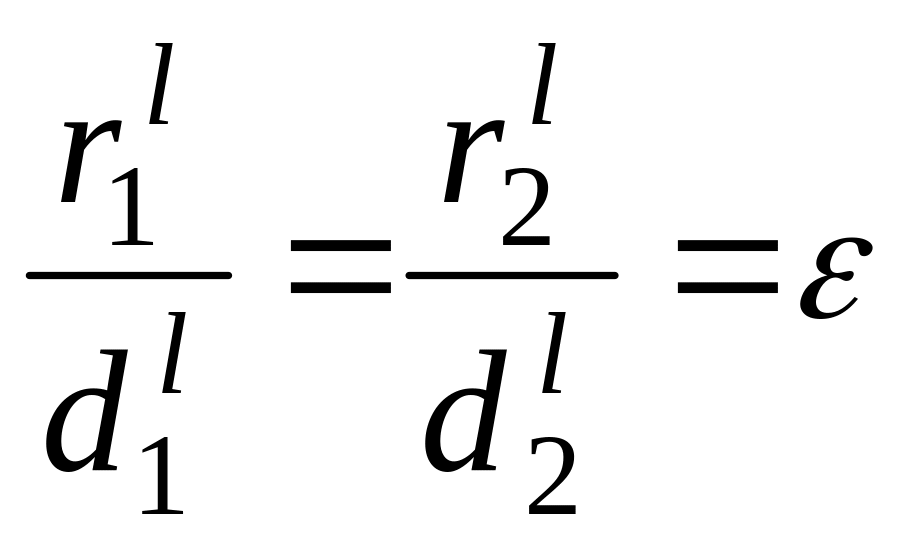Навпаки, нехай – точка площини, яка лежить на відстані від фокуса і на відстані від відповідної йому директриси гіперболи (26), причому . Покажемо, що точка належить гіперболі. Відстань від точки до фокуса обчислимо як відстань між двома точками за формулою , а відстань – як відстань від точки до прямої-директриси , заданої нормальним рівнянням , так що . Тоді

.

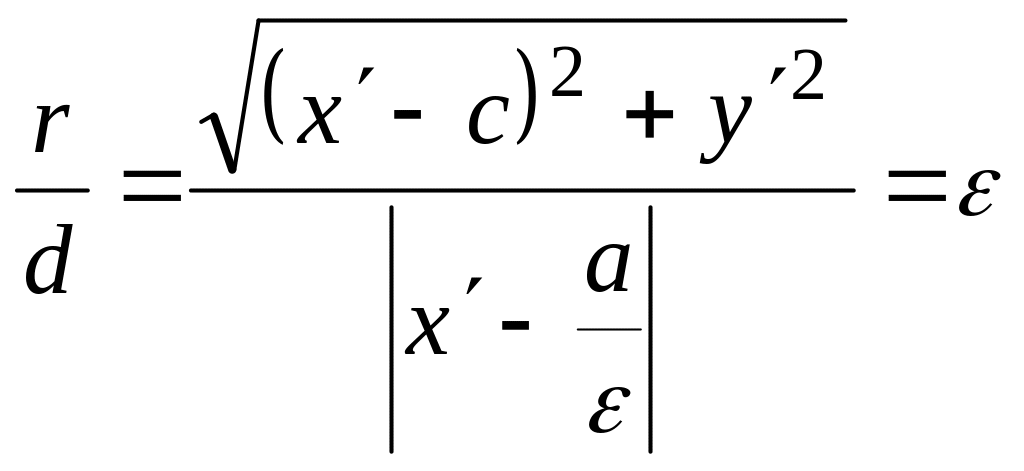Звідси,

;

;

;

;

;

,

тобто координати точки задовольняють рівняння гіперболи (26).

Вправа. Показати, що якщо , де – відстань від точки до фокуса , а – відстань від точки до відповідної йому директриси , то точка належить гіперболі (26).

8. Дотична до гіперболи. Для знаходження дотичної до гіперболи в її точці використаємо рівняння прямої з кутовим коефіцієнтом, що проходить через задану точку

. (27)

Для дотичної . Будемо шукати диференціюванням рівняння гіперболи (26):

.

Звідси,

.

Зокрема,

.

Підставимо в (27)

;

;

;

;

.

Оскільки точка належить гіперболі, то і рівняння дотичної до гіперболи набуває такого вигляду

.

9. Спряжені гіперболи. Дві гіперболи, визначені рівняннями і в одній і тій самій прямокутній декартовій системі координат з одними й тими самими значеннями півосей та , називаються спряженими.

Зазначимо, що гіпербола, для якої , називається рівносторонньою.