§ 2.2 Спектры некоторых импульсных сигналов

Рассмотрим некоторые конкретные примеры использования преобразования Фурье для анализа импульсных сигналов.

1 Одиночный прямоугольный импульс. Пусть имеется прямоугольный импульс длительностью и амплитудойh (рис.2.3).

Для такого импульса прямым преобразованием Фурье находим

(2.2.1)

где – площадь импульса. График этого спектра для положительных частот показан на рис. 2.3. Спектральная плотность обращается в нуль при, а при ω=0,s(ω)=q.

Замечаем, что при уменьшении длительности импульса функция s(ω) растягивается, т. е. ширина спектра увеличивается. При увеличении ширина спектра уменьшается.

Если ограничить спектр прямоугольного импульса первым нулем спектральной плотности, т.е. круговой частотой , то для произведения длительности импульсана ширину спектраполучим

Это равенство является частным случаем более общего равенства справедливого для всех импульсных сигналов:

(2.2.2)

согласно которому произведение ширины спектра сигнала на его длительность есть величина постоянная, близкая к единице. Существует несколько определений длительности импульса и ширины спектра. Согласно одному из них под длительностью импульса (шириной спектра) понимается промежуток времена (полоса частот), в котором сосредоточена подавляющая часть энергии импульса.

2 Колокольный (гауссов) импульс. Колокольным называется импульс, который описывается функцией

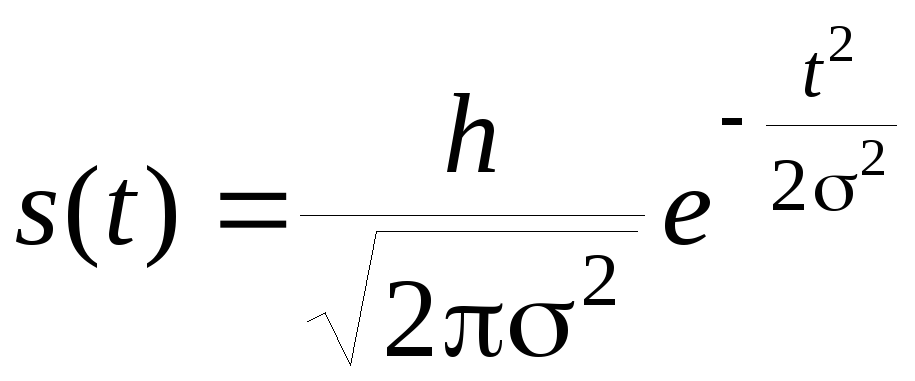(2.2.3)

Для спектральной плотности такого импульса с использованием преобразования Фурье получим

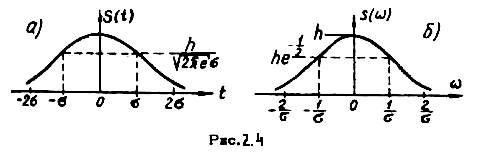
(2.2.4)

Графики колокольного импульса и модуля его спектра показаны на рис. 2.4.

Первой особенностью такого импульса является то, что спектральная плотность его совпадает по форме с временной функцией, т.е. является также гауссовой кривой. Другой особенностью такого импульса является то, что из всех возможных форм импульсов он имеет наименьшее произведение длительности на ширину спектра

3 Единичный импульс. Единичным импульсом или дельта-функцией называется функция бесконечно малой длительности с конечной площадью, равной единице:

Такую функцию можно рассматривать как предел прямоугольного импульса с длительностью τ и высотой при. Устремляя в (2.2.1), для спектральной плотности единичного импульса получим

(2.2.5)

Этот же результат можно получить и обычным способом:

(2.2.5')

так как при всех значениях, а приэкспоненциальный множитель обращается в единицу. Здесь использовалось так называемое фильтрующее свойство δ-функции, согласно которому

(2.2.6)

Таким образом, спектр единичного импульса является сплошным и равномерным с единичной спектральной плотностью вплоть до бесконечно больших значений частоты.

Единичный импульс является математической абстракцией. Физически можно реализовать только короткий импульс, т.е. импульс очень малой длительности τ, с площадью, равной q. Спектр такого импульса определятся выражением

При малых τ величина и

(2.2.7)

Следовательно, короткий импульс любой формы имеет равномерный спектр вплоть до частот порядка (пока выполняется условие). Далее спектральная плотность начинает убывать.

4 Единичная функция. Единичная функция, единичный скачок или функция включения записывается в виде

(2.2.8)

Заметим, что рассмотренный ранее единичный импульс можно рассматривать как производную единичной функции:

а единичную функцию можно выразить интегральным соотношением

(2.2.9)

Используя теорему о спектре интеграла (2.1.31) а выражение (2.2.5), получим

(2.2.10)

Модуль спектра этой функции есть . Зависимость его от частоты показана на рис.2.5 б.

Единичная функция широко используется в качестве испытательного сигнала при исследовании переходных процессов в электрических цепях. Напомним, что отклик цепи h(t) на единичную функцию называется переходной характеристикой.

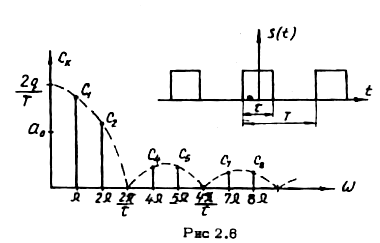
5 Периодическая последовательность прямоугольных импульсов. Рассмотрим

пульсов. Рассмотрим периодическую последовательность прямоугольных импульсов с длительностью τ и периодом Т (Рис.2.6). Используя (2.1.13). для такой последовательности получим

(2.2.11)

Этот же результат можно было бы получить и из выражения (2.2.1) используя соотношение (2.1.26), согласно котором спектральная плотность s(ω) одиночного импульса длительностью τ точностью до постоянного множителя совпадает с огибающей спектра амплитуд периодической последовательности таких же импульсов с периодом следованияТ. График модуля спектра (2.2.1) для положительных частот показан на рис.2.6.

На основании (2.1.11) и (2.2.11) периодическая последовательность прямоугольных импульсов разлагается в ряд Фурье следующим образом

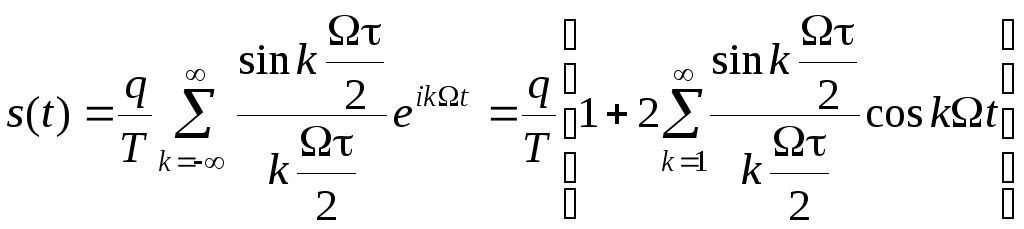(2.2.12)

Отметим теперь следующее обстоятельство. Если при неизменной длительности импульса увеличивается период Т последовательности, то расстояние между спектральными линиями уменьшается, расстояние же между нулями огибающей спектра, равноеостается неизменным. При неизменной длительности периодаТ и изменении длительности импульса будет меняться расстояние между нулями огибающей спектра.

Число гармоник, укладывающихся в интервале или между любыми двумя соседними нулями, будет определяться величиной

(2.2.13)

Величина Q, равная отношению длительности периода к длительности импульсов, называется скважностью периодической импульсной последовательности.

6 Одиночный радиоимпульс. Радиоимпульсом называется импульс, временная функция которого записывается в виде

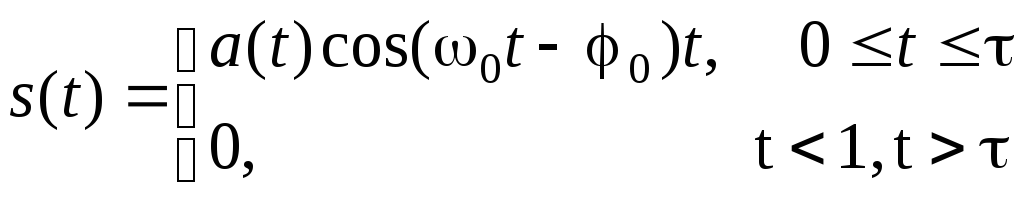(2.2.14)

где τ - длительность импульса, a(t) – огибающая амплитуд, - частота, а - начальная фаза высокочастотного колебания, период которого. Спектральная плотность радиоимпульса в соответствии с (2.1.19) будет равна

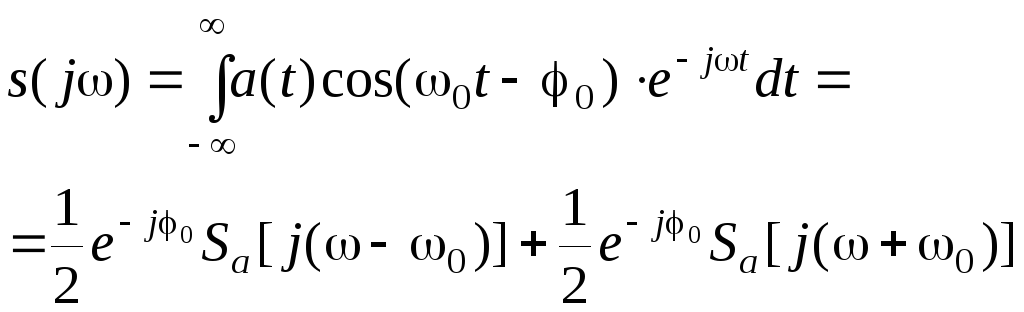(2.2.15)

где

(2.2.16)

– спектральные плотности огибающей импульса a(t), смещенные по оси частот на постоянную величину (ср.с (2.1.30)).

Таким образом, спектральная плотность радиоимпульса полностью определится спектральной плотностью его огибающий. Можно показать, что при идля большинства радиоимпульсов выполняется условие

(2.2.17)

Поэтому с достаточной точностью спектральную плотность одинокого радиоимпульса можно определять по формуле

(2.2.18)

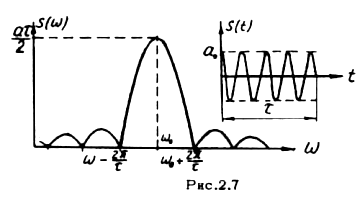
Проиллюстрируем сказанное на примере радиоимпульса с прямоугольной огибающей (рис.2.7):

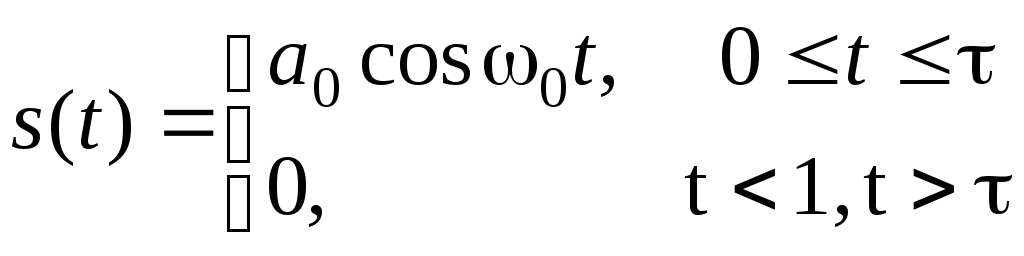(2.2.19)

Из (2.2.15) и (2.2.16) получим

(2.2.20)

откуда для модуля и фазы спектральной плотности находим

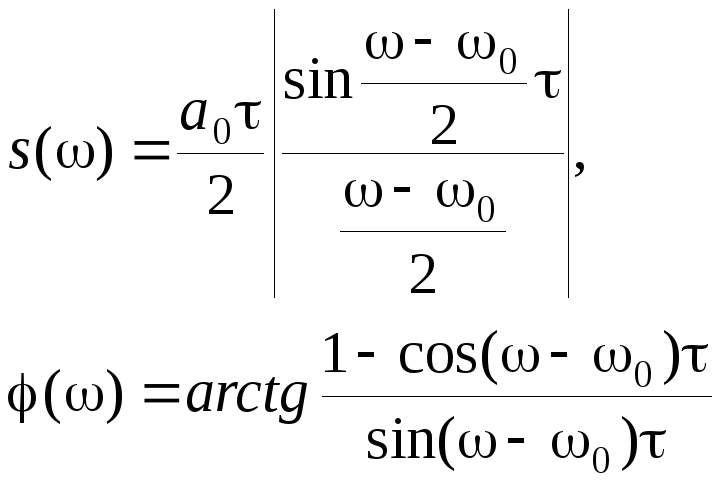
(2.2.21)

График модуля спектральной плотности показан на рис. 2.7

Как и следовало ожидать, отрезок гармонического колебания имеет сплошной спектр. При неограниченном увеличении длительности импульса τ получим гармоническое колебание в точном смысле определения периодическое функции. Сплошной спектр колебания при этом вырождается в одну спектральную линию на частоте .